目录
选择题
编程题
1.消失的数字
方法1：辅助数组法
方法2：位运算法
方法3：求和相减法
2.轮转数组
方法1：额外数组法
方法2：数组翻转法
选择题
1.给定一个整数sum，从有N个有序元素的数组中寻找元素a，b，使得a+b的结果最接近sum，最快的平均时间复杂度是（ ）
A.O(n)
B.O(n^2)
C.O(nlog2(n))
D.O(log2(n))
解析：
此题目中，数组元素有序，所以a,b两个数可以分别从开始和结尾处开始搜，根据首尾元素的和是否大于sum,决定搜索的移动，整个数组被搜索一遍，就可以得到结果，所以最好时间复杂度为n
2.如果一个函数的内部中只定义了一个二维数组a[3][6]，请问这个函数的空间复杂度为（ ）
A.O(n)
B.O(n^2)
C.O( 1 )
D.O(m*n)
答案：C
解析：函数内部数组的大小是固定的，不论函数运行多少次，所需空间都是固定大小的，因此空间复杂度为O(1)
3.分析以下函数的空间复杂度
public static int[][] get2Array(int n){int[][] array = new int[n][];for(int i = 0; i < n; i++) {array[i] = new int[n-i];n--;}return array;
}解析：
第0行n个int的空间
第1行n-1个int的空间
第2行n-2个int的空间
...
第n-1行1个元素的空间
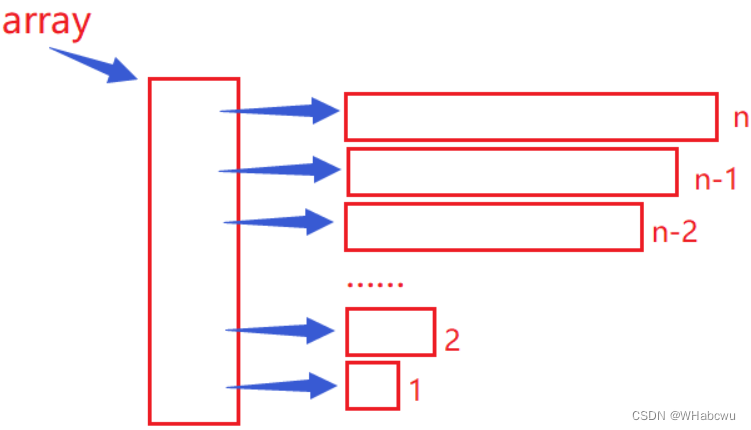
空间总的个数为：1+2+3+...+N-1 + N + N = (1+N)*N/2 + N = N^2/2 + 3N/2
采用大O渐进发表示就是：O(N^2)
故选择C
编程题（小练一手）
1.消失的数字
面试题 17.04. 消失的数字
https://leetcode.cn/problems/missing-number-lcci/
方法1：辅助数组法
public int missingNumber(int[] nums) {int[] arr = new int[nums.length + 1];for (int i = 0; i < nums.length; i++) {arr[nums[i]] = 1;}int i = 0;for (; i < arr.length; i++) {if (arr[i] == 0) {break;}}return i;}解析：
（1）首先遍历数组 nums，将数组中的每个元素作为辅助数组arr的下标，存放整数1。
（2）然后依次检查从 0到 n 的每个整数是否在辅助数组中，不在辅助数组中的数字即为消失的数字。
方法2：位运算法
public int missingNumber(int[] nums) {int flag = 0;for (int i = 0; i < nums.length; i++) {flag^=nums[i];}for (int i = 0; i <=nums.length; i++) {flag^=i;}return flag;}解析：
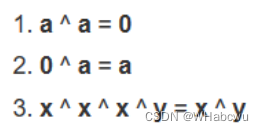
利用异或运算两次遍历可以算出消失的数字
方法3：求和相减法
public int missingNumber(int[] nums) {int sum1=0,sum2=0;for (int i = 0; i < nums.length; i++) {sum1+=nums[i];}for (int i = 0; i <=nums.length; i++) {sum2+=i;}return sum2-sum1;}解析：
将数组 nums 的元素之和记为 sum1,1到nums.length之和记为 sum2。sum1 比sum2 消失的一个数字，因此消失的数字即为sum2-sum1 之差。
2.轮转数组
189. 轮转数组https://leetcode.cn/problems/rotate-array/
方法1：额外数组法
class Solution {public void rotate(int[] nums, int k) {int sz=nums.length;int[] arr = new int[sz];for (int i = 0; i < sz; i++) {arr[(i+k)%sz]=nums[i];}System.arraycopy( arr, 0, nums, 0, sz);}
}解析：
我们可以使用额外的数组来将每个元素放至正确的位置。用 size 表示数组的长度，我们遍历原数组，将原数组下标为 i 的元素放至新数组下标为 (i+k)%size 的位置，最后将新数组拷贝至原数组即可。
方法2：数组翻转法
思路如下：
- 首先对整个数组实行翻转。
- 这时候，从 k 处分隔数组，左右两数组，各自进行翻转即可。
class Solution {public void rotate(int[] nums, int k) {int sz=nums.length;k%=sz;reverse(nums,0,sz-1);reverse(nums,0,k-1);reverse(nums,k,sz-1);}public void reverse(int[] nums, int start, int end) {while (start<end){int tmp=nums[start];nums[start]=nums[end];nums[end]=tmp;start++;end--;}}
}以上为我个人的小分享，如有问题，欢迎讨论！！！
都看到这了，不如关注一下，给个免费的赞 
