巴特沃斯、切比雪夫I型、切比雪夫Ⅱ型和椭圆型滤波器的相同和不同之处

1、概述 

      用 MATLAB 中的函数可以设计巴特沃斯、切比雪夫I型、切比雪夫Ⅱ型和椭圆型滤波器，我们用MATLAB的函数，在相同的条件下观察巴特沃斯、切比雪夫I型、 切比雪夫Ⅱ型和椭圆型滤波器，再进一步比较它们的相同和不同之处。 

2、实例 

例：设计一个模拟带通滤波器，带通值为wp1=0.2π，wp2=0.3π，带阻值ws1=0.1π，ws2=0.4，Rp=1，Rs=20。对这些指标分别以巴特沃斯、切比雪夫I型、切比雪夫Ⅱ型和椭圆型设计四类模拟滤波器。

Matlab 程序如下：

% 用 MATLAB 中的函数可以设计巴特沃斯、切比雪夫I型、切比雪夫型和椭圆型滤波器，
% 我们用MATLAB的函数，在相同的条件下，观察巴特沃斯、切比雪夫I型、 切比雪夫Ⅱ型和椭圆型滤波器，
% 再进一步比较它们的相同和不同之处。?
% 
% 例：设计一个模拟带通滤波器，带通值为wp1=0.2π，wp2=0.3π，
% 带阻值ws1=0.1π，ws2=0.4，Rp=1，Rs=20。
% 对这些指标分别以巴特沃斯、切比雪夫I型、切比雪夫Ⅱ型和椭圆型设计四类模拟滤波器。
% 
% pr3_2_1
clear; close all; clc;wp = [0.2*pi 0.3*pi];   % 设置通带频率
ws = [0.1*pi 0.4*pi];   % 设置阻带频率
Rp = 1; Rs = 20;        % 设置波纹系数
% 巴特沃斯滤波器设计
[N,Wn] = buttord(wp,ws,Rp,Rs,'s'); % 求巴特沃斯滤波器阶数
fprintf('巴特沃斯滤波器 N=%4d\n',N) % 显示滤波器阶数
[bb,ab] = butter(N,Wn,'s');        % 求巴特沃斯滤波器系数
W= 0:0.01:2; % 设置模拟频率
[Hb,wb] = freqs(bb,ab,W); % 求巴特沃斯滤波器频率响应
plot(wb/pi, 20*log10(abs(Hb)),'b')% 作图
hold on% 切比雪夫I型滤波器设计
[N,Wn] = cheb1ord(wp,ws,Rp,Rs,'s');   % 求切比雪夫I型滤波器阶数
fprintf('切比雪夫I型滤波器 N=%4d\n',N) % 显示滤波器阶数
[bc1,ac1] = cheby1(N,Rp,Wn,'s');     % 求切比雪夫I型滤波器系数
[Hc1,wc1] = freqs(bc1,ac1,W);        % 求切比雪夫I型滤波器频率响应
plot(wc1/pi, 20*log10(abs(Hc1)),'k')% 作图% 切比雪夫II型滤波器设计 
[N,Wn] = cheb2ord(wp,ws,Rp,Rs,'s');  % 求切比雪夫II型滤波器阶数
fprintf('切比雪夫II型滤波器 N=%4d\n',N) % 显示滤波器阶数
[bc2,ac2] = cheby2(N,Rs,Wn,'s');    % 求切比雪夫II型滤波器系数
[Hc2,wc2] = freqs(bc2,ac2,W);       % 求切比雪夫II型滤波器频率响应
plot(wc2/pi, 20*log10(abs(Hc2)),'r')% 作图% 椭圆型滤波器设计
[N,Wn] = ellipord(wp,ws,Rp,Rs,'s');  % 求椭圆型滤波器阶数
fprintf('椭圆型滤波器 N=%4d\n',N) % 显示滤波器阶数
[be,ae] = ellip(N,Rp,Rs,Wn,'s');     % 求椭圆型滤波器系数
[He,we] = freqs(be,ae,W);            % 求椭圆型滤波器频率响应
% 作图
plot(we/pi, 20*log10(abs(He)),'g')
axis([0 max(we/pi) -30 2]); %grid;
legend('巴特沃斯滤波器','切比雪夫I型滤波器','切比雪夫II型滤波器','椭圆型滤波器')
xlabel('角频率{\omega}/{\pi}'); ylabel('幅值/dB')
set(gcf,'color','w'); line([0 max(we/pi)],[-20 -20],'color','k','linestyle','--');
line([0 max(we/pi)],[-1 -1],'color','k','linestyle','--');
line([0.2 0.2],[-30 2],'color','k','linestyle','--');
line([0.3 0.3],[-30 2],'color','k','linestyle','--');

巴特沃斯滤波器 N=   4
切比雪夫I型滤波器 N=   3
切比雪夫II型滤波器 N=   3
椭圆型滤波器 N=   2

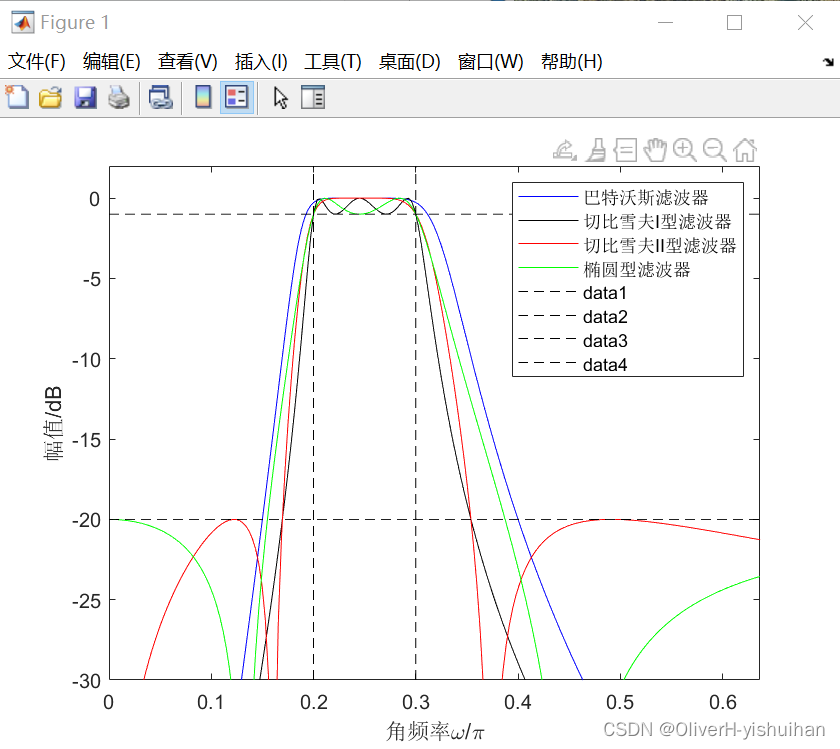
3、讨论 

• ①我们对设计模拟滤波器的要求是：带通为wp1=0.2，wp2=0.3，带阻为ws1=0.1π，ws2=0.4π，Rp=1，Rs=20。在上图中0.2和0.3(单位为pi)处画了两条竖虚线，可以看出这四类带通滤波器通带区间都在0.2~0.3之内。又在纵坐标-1dB和-20dB 处画了两条横虚线，也可以看出通带内起伏在-1~0dB之间，阻带都小于或等于-20dB。这说明四类滤波器的幅频响应曲线形状虽不完全相同,但都满足了初始设计的要求。 
• ②在运行程序时把每个滤波器的阶数都显示了出来，可以看到，在满足相同的设计要求的条件下，巴特沃斯滤波器用了4阶，阶数最多；切比雪夫I型滤波器和切比雪夫Ⅱ型滤波器用了3阶；椭圆型滤波器用了2阶，阶数最少。阶数少，相应的滤波器系数就少，在实现时就能减小运算量。 
• ③从图中可看出，巴特沃斯和切比雪夫Ⅱ型滤波器在通带是平坦的，切比雪夫 I型和椭圆型滤波器在通带有波纹，而切比雪夫Ⅱ型和椭圆型滤波器在阻带有波纹。 
• ④从图中还可看出，在满足相同的设计要求的条件下，切比雪夫Ⅱ型滤波器和 椭圆型滤波器在过渡带内衰减更陡。