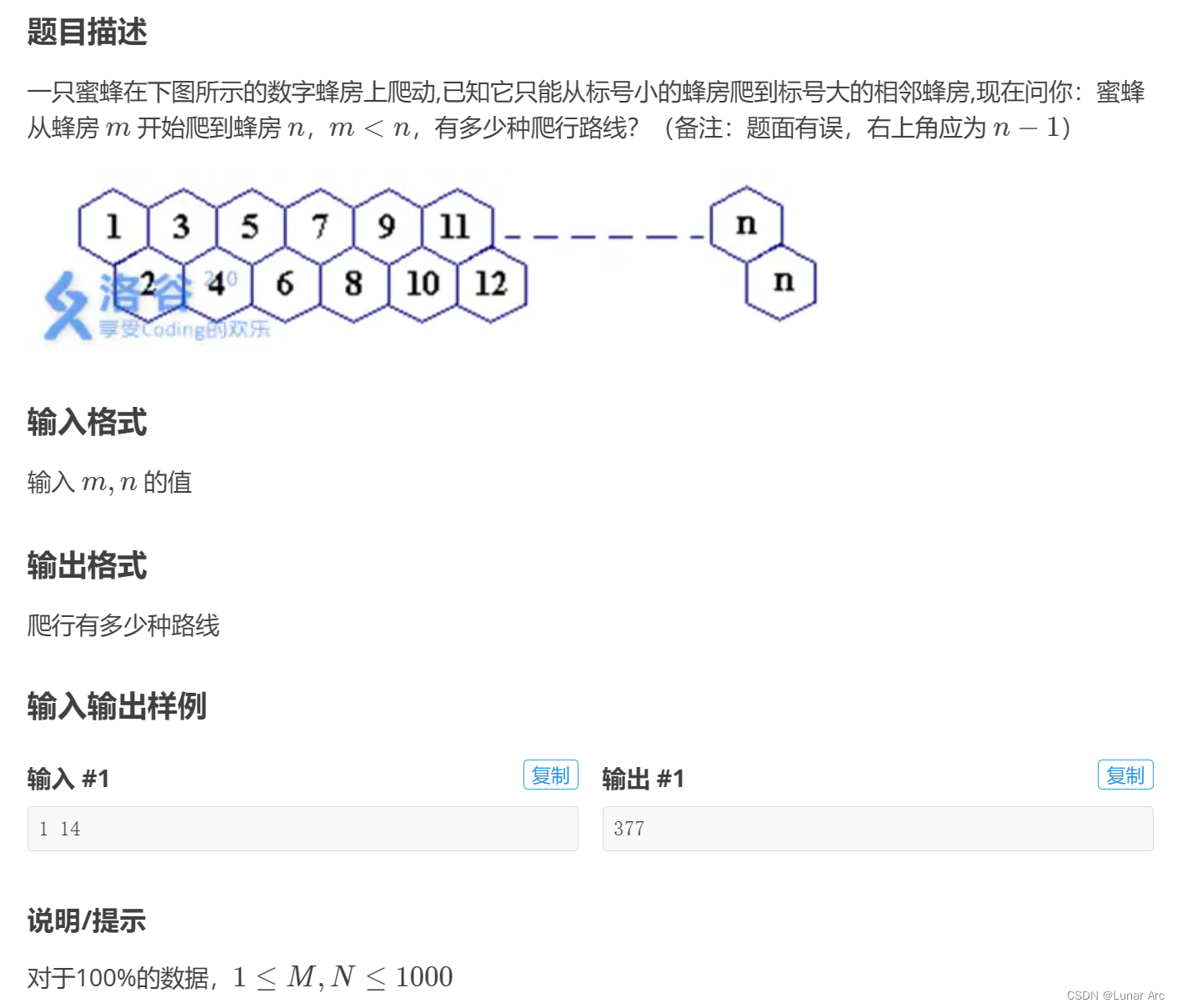
题目

luogu P2437 蜜蜂路线

解题思路

最初只觉得是一道很简单的递推

先考虑从第一个点出发的情况，对于第 $k (k \geq 3)$ 个点，路线数表示如下：
$a [k] = a [k - 1] + a [k - 2]$ 接下来我们开始考虑不从第一个点开始的情况，即从第 $m$ 个点到第 $n$ 个点的路线数，可以平替为从第 $1$ 个点到第 $n - m + 1$ 个点的爬行路线。

对你想的没错，就是我们熟悉的斐波那契数列，当我最初看到数据范围 $n, m \leq 1000$ 时我不以为意，但上去就WA了，意识到事情不对了。
我们要意识到，斐波那契的第1000项是这个数字：

43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875

不会高精度的我陷入了沉思… …

还好看到了一位 $d a l a o$ 为纯小白准备的解决方案

问题解决

我们准备一个二维数组 $f [i] [j]$ ，表示第1个点到第 $i$ 个点的路线数的第 $j$ 位的数字是 $f [i] [j]$ 。

对于第 $i$ 个点 $f [i] [j]$ 的计算方式如下：

void ad(int x)
{int i;for(i=1;i<=len;++i) f[x][i]=f[x-1][i]+f[x-2][i];for(i=1;i<=len;++i){if(f[x][i]>9){f[x][i+1]+=f[x][i]/10;f[x][i]%=10;}}if(f[x][len+1]) len++;
}

逢十进一，通俗易懂

这样就能让每一个 $f [i] [j]$ 都只储存一位数字，不用害怕超过储存范围的问题。最大的 $ma x n u m$ 有几位，第二维度开多大即可。

代码实现

#include<stdio.h>
#include<math.h>
#include<stdlib.h>
#include<string.h>
int m,n,len=1; 
int f[1005][1005];
void ad(int x)
{int i;for(i=1;i<=len;++i) f[x][i]=f[x-1][i]+f[x-2][i];for(i=1;i<=len;++i){if(f[x][i]>9){f[x][i+1]+=f[x][i]/10;f[x][i]%=10;}}if(f[x][len+1]) len++;
}
int main()
{scanf("%d%d",&m,&n);f[1][1]=1; f[2][1]=1;int i;for(i=3;i<=n-m+1;++i)	ad(i);for(i=len;i;i--) printf("%d",f[n-m+1][i]);return 0;
}