2023icpc网络赛第一场 I
题意:题目给出只包含大小写字母,数字以及'?'的字符串,对于每一个小写字母,这一位字符既有可能是该小写字母,也有可能是该小写字母的对应大写字母,也就是该位的字符有两种可能,对于问号,可能是所有大写字母或者所有小写字母,或者所有单数字,则共有62种情况,而对于大写字母和数字位则都是确定的只有这一种情况
要求输出最后符合以下条件的字符串共有多少种
1、至少有一个小写字母
2、至少有一个大写字母
3、至少有一个数字位
4、相邻的两个字符不能相同
思路:容斥原理+线性dp
我们暂且先不管前三个要求,对于要求4,可以通过线性dp来解决,我们定义dp[i][j]为以第i位为结尾并且结尾这一位选择j(定义1-26代表大写字母,27-52为小写字母,53-62为数字位,63代表该位的所有情况的总和,63最后单独处理)共有多少种情况,则对于某一位选某一个字符的情况数即为前一位的总情况数减去前一位也选相同字符的情况数,则有状态转移方程:
然而题目中给出了对于内存的限制,通过观察不难发现每一次状态更新只与前一层有关,所以考虑将dp数组降维
此时我们再来解决前三个条件,对于之前提到的线性dp,我们可以得到在不考虑大小写字母以及数字位是否都存在的所有符合条件4的合法情况数,但其中是存在违反条件1-3的情况的,我们现在要做的是将这些情况不重不漏(划重点)的减去,这样我们就可以得到最终结果,这时就要应用到容斥原理:
我们将这些情况(已知所有符合条件4的情况中违反条件1-3的所有情况)抽象成以下图形,其中圈1为一定不包括大写字母的所有情况,圈2为一定不包括小写字母的所有情况,圈3为一定不包括数字位的所有情况,那么现在问题就是要求出这三个圆的共同覆盖面积并减去,
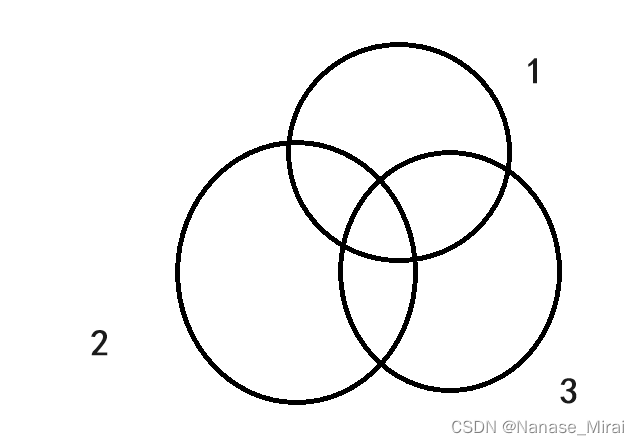
这时我们通过规定是否一定不存在大写字母、小写字母或者数字位对线性dp进行限制并求得在该条件下的情况数,具体实现方式见代码
而当我们分别减去一定不存在大写字母,一定不存在小写字母,一定不存在数字位这三种情况的方案数之后,对于该图形中的每个小图形具体减了几次见下图
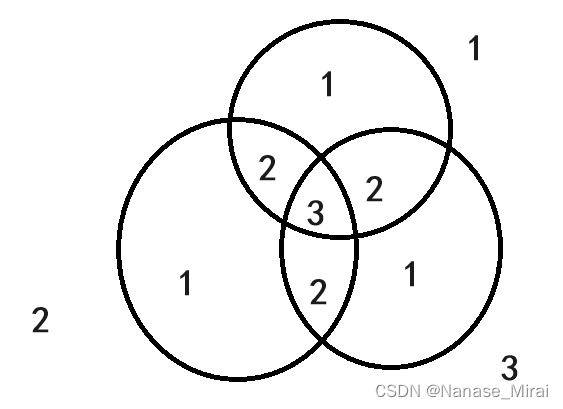
这时我们又发现中间有一部分多减了,所以我们又要将部分图形给加回来,此时我们发现可以通过加每两个圆的公共部分来将结果进一步推进,对于一定不存在大写字母并且一定不存在数字位的图形范围为:
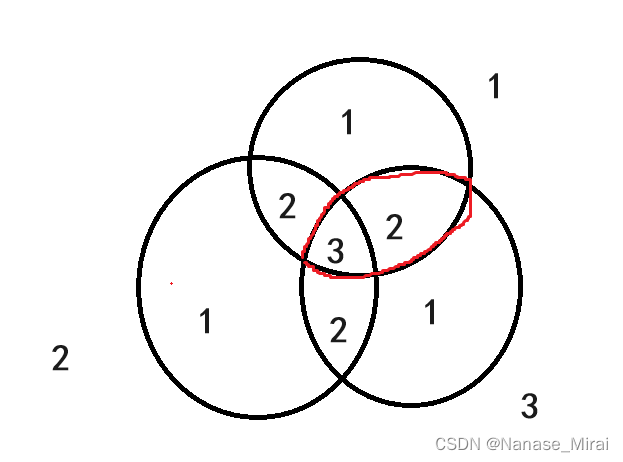
将三个圆的两两公共部分都加回来之后对于每个小图形的减去次数可表示为:
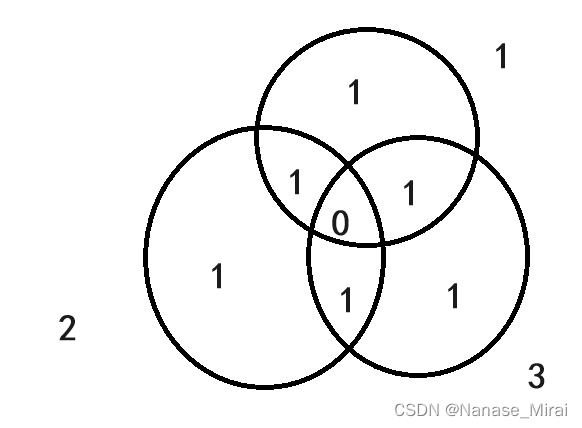
此时我们不难发现只需要将三种字符都一定不存在的情况减去就可以了(实际上这部分根本不存在,所以减不减无所谓)
最后的效果:
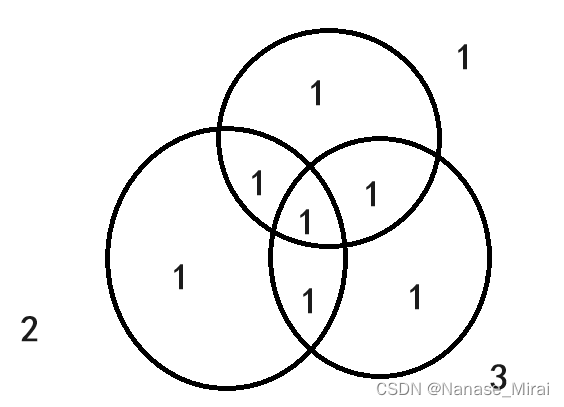
ac代码:
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define INF 0x3f3f3f3f
#define pb push_back
#define int long long
// #define int unsigned long long
#define Mirai ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
using namespace std;
typedef pair<int,int> pii;
const int N=1e5+10,mod=998244353;
int dp[2][100];//1-26 大写字母 27-52 小写字母 53-62 数字 63 总和
int b[3];
int n;
string s;
int get()
{memset(dp,0,sizeof dp);dp[0][63]=1;for(int i=1;i<=n;i++){for(int j=1;j<=63;j++)dp[i&1][j]=0;if(s[i]>='A'&&s[i]<='Z')//大写{if(b[0])return 0;dp[i&1][s[i]-'A'+1]=dp[(i-1)&1][63]-dp[(i-1)&1][s[i]-'A'+1];}else if(s[i]>='0'&&s[i]<='9')//数字{if(b[2])return 0;dp[i&1][s[i]-'0'+53]=dp[(i-1)&1][63]-dp[(i-1)&1][s[i]-'0'+53];}else if(s[i]>='a'&&s[i]<='z')//小写{if(b[0]&&b[1])return 0;if(!b[1])dp[i&1][s[i]-'a'+27]=dp[(i-1)&1][63]-dp[(i-1)&1][s[i]-'a'+27];if(!b[0])dp[i&1][s[i]-'a'+1]=dp[(i-1)&1][63]-dp[(i-1)&1][s[i]-'a'+1];;}else //问号{ for(int j=1;j<=62;j++){if(b[0]&&j>=1&&j<=26)continue;if(b[1]&&j>=27&&j<=52)continue;if(b[2]&&j>=53)continue;dp[i&1][j]=dp[(i-1)&1][63]-dp[(i-1)&1][j];}}for(int j=1;j<=62;j++)(dp[i&1][63]+=dp[i&1][j]%mod)%=mod;}return dp[n&1][63];
}
void solve()
{cin>>n;cin>>s;s=" "+s;int sum=get();b[0]=1,b[1]=0,b[2]=0,sum-=get();b[0]=0,b[1]=1,b[2]=0,sum-=get();b[0]=0,b[1]=0,b[2]=1,sum-=get();b[0]=1,b[1]=1,b[2]=0,sum+=get();b[0]=1,b[1]=0,b[2]=1,sum+=get();b[0]=0,b[1]=1,b[2]=1,sum+=get();// b[0]=1,b[1]=1,b[2]=1,sum-=get();//都不存在的情况,实际上这部分一定为0cout<<(sum%mod+mod)%mod<<endl;
}
signed main()
{Mirai;int T=1;//cin>>T;while(T--){solve();}
}