Python绘制X-bar图和R图 | 统计过程控制SPC-编程知识

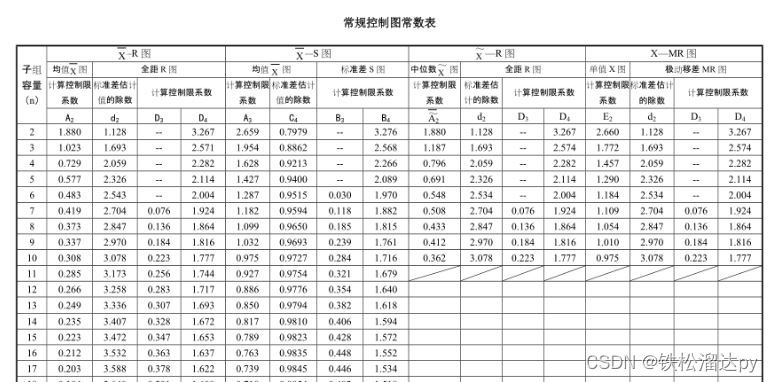
X-bar图和R图是用于统计过程控制（SPC）的两种常用工具，用于监测过程的平均值和范围（变异性）。这些图有助于识别过程中的变化和异常，以便及时采取纠正措施。

**X-bar图（平均值控制图）**显示了一系列样本的平均值，用于监测过程的平均值是否保持在可接受的范围内。X-bar图通常由以下几个要素组成：

样本平均值：每个样本的数据点的平均值，通常用于每个样本的数据集。
中心线：通常是所有样本平均值的平均值，表示过程的目标值。
控制限：通常包括上限控制限和下限控制限，用于指示过程平均值的可接受范围。控制限的计算方法可以根据需求不同而有所不同，常用的方法包括使用标准偏差和样本大小。
数据点：每个样本的平均值在X-bar图上以数据点的形式表示，通常用线连接这些数据点以显示趋势。

**R图（范围控制图）**显示了一系列样本的范围（最大值和最小值之间的差异），用于监测过程的变异性。R图通常由以下几个要素组成：

范围（R）：每个样本的最大值和最小值之间的差异。
中心线：通常是所有R值的平均值，表示过程的变异性目标。
控制限：通常包括上限控制限，用于指示R值的可接受范围。控制限的计算方法可以根据需求不同而有所不同，常用的方法包括使用标准偏差和样本大小。
数据点：每个样本的R值在R图上以数据点的形式表示，通常用线连接这些数据点以显示趋势。

在绘制X-bar图和R图之前，需要进行以下步骤：

收集样本数据并确定样本大小和采样频率。
计算每个样本的平均值（X-bar图）和范围（R图）。
计算X-bar图和R图的中心线和控制限。
绘制X-bar图和R图，并将样本数据点与中心线和控制限一起显示。

要生成表格数据并写入文件，然后读取数据并计算X-bar图和R图所需的平均值、标准差等，您可以按照以下步骤进行操作。首先，确保您已经安装了NumPy、matplotlib和Pandas库。

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 防止中文标签乱码，还有通过导入字体文件的方法
plt.rcParams['axes.unicode_minus'] = False# 生成随机数据，例如，生成5个样本，每个样本5个数据点
data = np.random.rand(5, 5)# 创建一个Pandas DataFrame
df = pd.DataFrame(data, columns=['Sample 1', 'Sample 2', 'Sample 3', 'Sample 4', 'Sample 5'])# 将数据写入CSV文件
df.to_csv('sample_data.csv', index=False)# 从CSV文件读取数据
df = pd.read_csv('sample_data.csv')# 打印数据框的前几行以确保数据已成功加载
print(df.head())
# 计算每个样本的平均值
x_bar = df.mean(axis=1)# 计算每个样本的范围（R）
R = df.max(axis=1) - df.min(axis=1)# 计算平均值和R的平均值
x_bar_avg = x_bar.mean()
R_avg = R.mean()# 计算X-bar图的控制限（通常为平均值的上下控制限）
x_bar_upper_limit = x_bar_avg + 0.577 * R_avg
x_bar_lower_limit = x_bar_avg - 0.577 * R_avg# 计算R图的控制限（通常为R的上限）
R_upper_limit = R_avg * 2.114# 打印计算结果
print(f'X-bar平均值: {x_bar_avg}')
print(f'R平均值: {R_avg}')
print(f'X-bar控制限: ({x_bar_lower_limit}, {x_bar_upper_limit})')
print(f'R控制限: {R_upper_limit}')# 绘制X-bar图
plt.figure(figsize=(10, 6))
plt.plot(x_bar, marker='o', linestyle='-')
plt.axhline(y=x_bar_avg, color='r', linestyle='--', label='平均值')
plt.axhline(y=x_bar_upper_limit, color='g', linestyle='--', label='控制限')
plt.axhline(y=x_bar_lower_limit, color='g', linestyle='--')
plt.title('X-bar图')
plt.xlabel('样本编号')
plt.ylabel('平均值')
plt.legend()
plt.grid()
plt.show()# 绘制R图
plt.figure(figsize=(10, 6))
plt.plot(R, marker='o', linestyle='-')
plt.axhline(y=R_avg, color='r', linestyle='--', label='平均值')
plt.axhline(y=R_upper_limit, color='g', linestyle='--', label='控制限')
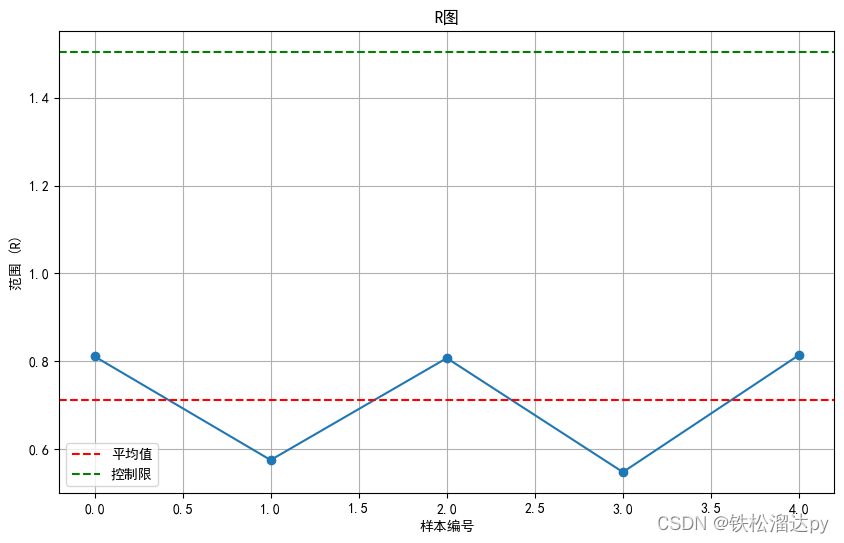
plt.title('R图')
plt.xlabel('样本编号')
plt.ylabel('范围 (R)')
plt.legend()
plt.grid()
plt.show()#    Sample 1  Sample 2  Sample 3  Sample 4  Sample 5
# 0  0.341066  0.113474  0.924694  0.877339  0.257942
# 1  0.659984  0.817222  0.555201  0.529651  0.241852
# 2  0.093103  0.897216  0.900418  0.633101  0.339030
# 3  0.349210  0.725956  0.897110  0.887086  0.779876
# 4  0.642032  0.084140  0.161629  0.898554  0.606429
# X-bar平均值: 0.568532531479609
# R平均值: 0.7112440409136231
# X-bar控制限: (0.1581447198724485, 0.9789203430867696)
# R控制限: 1.5035699024913993

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 防止中文标签乱码，还有通过导入字体文件的方法
plt.rcParams['axes.unicode_minus'] = False# 假设您已经有了样本数据，存储在x_bar_values和R_values中# 计算中心线和控制限
x_bar_centerline = np.mean(x_bar_values)
R_centerline = np.mean(R_values)
R_bar = np.mean(R_values)# 计算控制限（通常使用常见的控制图常数，如A2，D3，D4）
A2 = 0.729
D3 = 0
D4 = 2.282
x_bar_UCL = x_bar_centerline + A2 * R_bar
x_bar_LCL = x_bar_centerline - A2 * R_bar
R_UCL = D4 * R_bar
R_LCL = D3 * R_bar# 绘制X-bar图
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(x_bar_values, marker='o', linestyle='-')
plt.axhline(y=x_bar_centerline, color='r', linestyle='--', label='中心线')
plt.axhline(y=x_bar_UCL, color='g', linestyle='--', label='上限控制限')
plt.axhline(y=x_bar_LCL, color='g', linestyle='--', label='下限控制限')
plt.title('X-bar图')
plt.xlabel('样本编号')
plt.ylabel('平均值')
plt.legend()
plt.grid()# 绘制R图
plt.subplot(2, 1, 2)
plt.plot(R_values, marker='o', linestyle='-')
plt.axhline(y=R_centerline, color='r', linestyle='--', label='中心线')
plt.axhline(y=R_UCL, color='g', linestyle='--', label='上限控制限')
plt.title('R图')
plt.xlabel('样本编号')
plt.ylabel('范围 (R)')
plt.legend()
plt.grid()plt.tight_layout()
plt.show()

这段代码将生成X-bar图和R图，帮助您监控过程的平均值和范围，以便识别任何过程中的异常或变化。请根据您的数据和需求进行适当的修改。在实际应用中，您可能需要根据标准和过程的特性来调整控制限和常数。