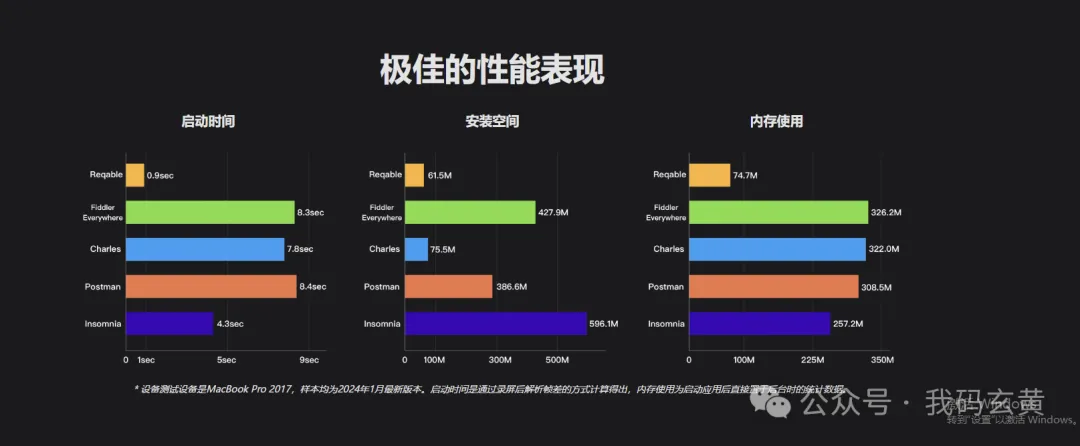
一般来说,莫队是一种比较优雅的暴力了……
说优雅一般分为两方面,一方面,莫队的时间复杂度是 \(\mathcal O(n\sqrt{n})\),这种时间复杂度一般不是最优解,但是能过,所以是暴力中的王子。
另一方面,莫队用途真的很广,我的老师曾说过:字符串、数论等等,如果你想用莫队做,都是可以做的。
然后他就举了一个例题。
给你 \(T\le 10^5\) 组数据,然后给你 \(n,m\le 10^5\),问你 \(\sum\limits_{i=0}^m\binom{n}{i}\)。
我想了半天,告诉老师可以分块,然后老师说分块和莫队差不多,然后我们展开了1h的辩论。
老师给我讲了精彩的莫队算法。
设 \(S_{n,m}=\sum\limits_{i=0}^m \binom{n}{i}\)。
则 \(S_{n,m}=S_{n,m-1}+\binom{n}{m}\)。
众所周知,莫队需要两个指针 \(l,r\) 的变动,那么有了 \(m\) 的变动,\(n\) 呢?
然后老师用惊人的观察力告诉我了一个显然的式子:
\[\begin{aligned}
& \because \binom{n}{m}=\binom{n-1}{m}+\binom{n-1}{m-1}\\\
& \therefore S_{n,m}=\binom{n}{0}+\cdots+\binom{n}{m}\\\
&=\binom{n-1}{0}+\binom{n-1}{0}+\binom{n-1}{1}+\cdots+\binom{n-1}{m-1}+\binom{n-1}{m-1}\\\
&=S_{n-1,m}+S_{n-1,m-1}\\\
&=2S_{n-1,m}-\binom{n-1}{m}
\end{aligned}
\]
此题终,复杂度 \(\mathcal O(n\sqrt{n})\)。
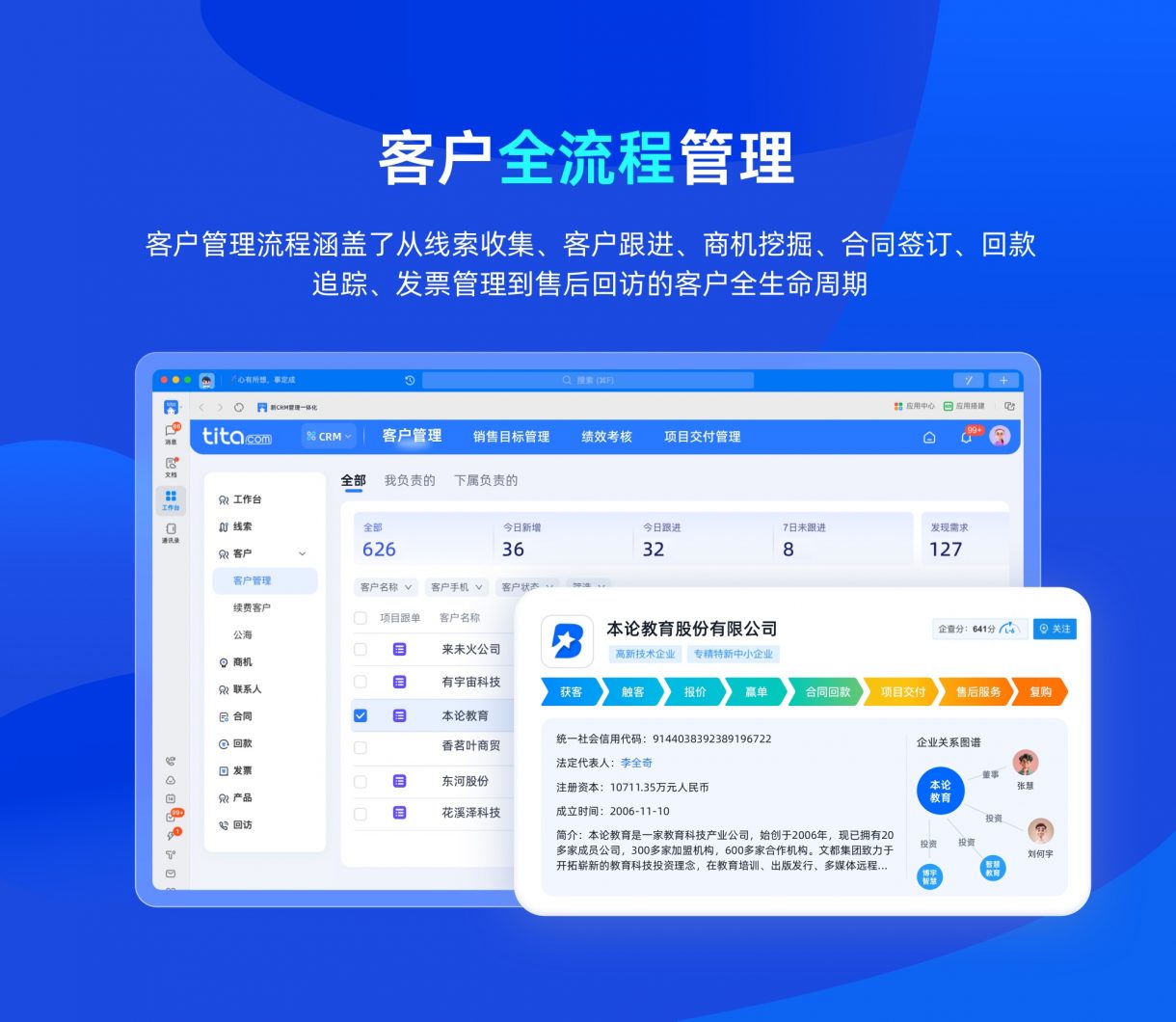


![[Tools] GitHub Action 部署文档网站](https://resource.duyiedu.com/xiejie/2023-06-09-063500.png)
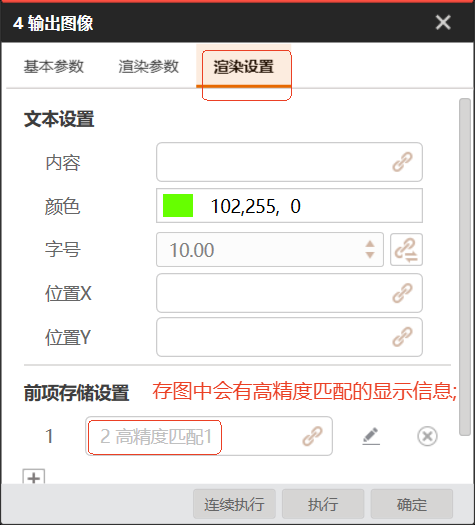
![[Tools] VitePress搭建文档网站](https://resource.duyiedu.com/xiejie/2023-06-09-024255.jpg)