目录

第一题

题目来源

题目内容

解决方法

方法一：迭代

方法二：模拟

方法三：循环模拟

方法四：传递

第二题

题目来源

题目内容

解决方法

方法一：回溯

方法二：枚举优化

第三题

题目来源

题目内容

解决方法

方法一：递归

方法二：迭代

方法三：动态规划

方法四：递推

---

第一题

题目来源

2582. 递枕头 - 力扣（LeetCode）

题目内容

解决方法

方法一：迭代

这个问题可以使用一个简单的循环来解决。我们使用两个变量来追踪当前拿着枕头的人的位置和传递的方向。

1. 首先，我们初始化forward为true，表示初始传递方向是向前的。然后，我们进入一个循环，从1到time进行迭代，模拟枕头传递的过程。
2. 在循环中，我们首先检查当前拿着枕头的人是否处于队列的首位（即pos == 1），如果是，则将传递方向设置为向前（forward = true）；然后，我们检查当前拿着枕头的人是否处于队列的末尾（即pos == n），如果是，则将传递方向设置为向后（forward = false）。
3. 接下来，我们根据传递方向更新当前拿着枕头的人的位置。如果传递方向是向前（forward = true），则将pos加1；如果传递方向是向后（forward = false），则将pos减1。
4. 重复这个过程，直到达到指定的传递时间time。最后，返回拿着枕头的人的编号pos。

总结来说，我们使用一个循环来迭代传递过程，并根据当前位置和传递方向进行更新，直到达到指定的传递时间。最终，返回拿着枕头的人的编号。

class Solution {public int passThePillow(int n, int time) {boolean forward = true;int pos = 1;for (int i = 1; i <= time; i++) {if (pos == 1) {forward = true;} else if (pos == n) {forward = false;}if (forward) {pos++;} else {pos--;}}return pos;}
}

复杂度分析：

• 时间复杂度分析：循环的次数取决于传递的时间time，因此循环的次数是常数级别的。所以，时间复杂度可以表示为O(1)，即常数时间复杂度。
• 空间复杂度分析：在这个算法中，并没有使用任何额外的数据结构，只使用了几个整型变量来追踪位置和方向。因此，空间复杂度是O(1)，即常数空间复杂度。

综上所述，该算法具有常数级别的时间复杂度和空间复杂度。这意味着无论输入的传递时间time和参与传递的人数n有多大，算法的执行时间和空间占用都是固定的。

LeetCode运行结果：

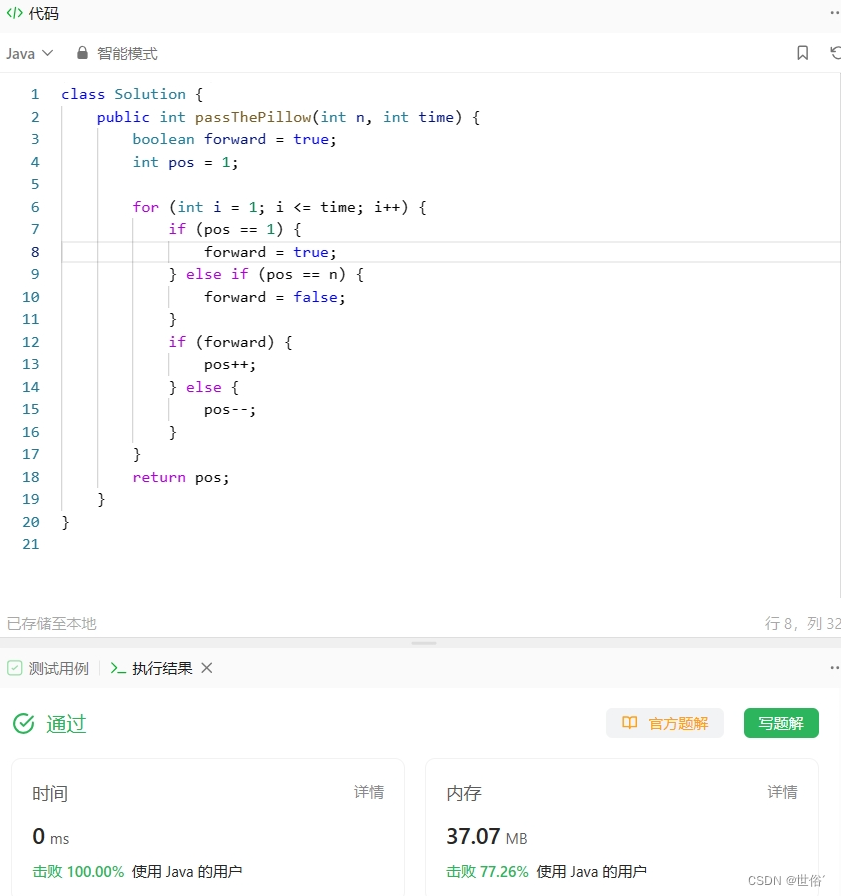
方法二：模拟

这个算法的思路是通过观察规律，找到一个公式计算出时间t后枕头所在位置的编号。

首先，我们可以注意到，每当枕头到达队伍的某一端，就会改变传递方向。也就是说，枕头的传递方向是周期性的，以(n-1)*2为一个周期。例如，当n=4时，第一次周期内，枕头的传递顺序是1-2-3-4-3-2；第二次周期内，枕头的传递顺序是2-3-4-3-2-1。因此，我们可以将time对于一个周期取模，以便更好地处理时间过长的情况。

接下来，考虑如何计算枕头所在位置的编号。如果time小于n，此时枕头仍然在最开始的n个人中间传递，因此枕头的位置等于time+1。否则，枕头已到达了队伍的另一端，需要反向传递。如果按顺序数枕头位置，此时与time相对应的枕头位置应该是n*2-time-1，因此可以使用这个表达式计算枕头所在的位置编号。

class Solution {public int passThePillow(int n, int time) {time %= (n - 1) * 2;return time < n ? time + 1 : n * 2 - time - 1;}
}

复杂度分析：

• 时间复杂度分析：在这个算法中，我们只有一个简单的求模运算和一个条件判断，所以时间复杂度为O(1)，即常数时间复杂度。
• 空间复杂度分析：该算法没有使用任何额外的数据结构或递归调用，所以空间复杂度为O(1)，即常数空间复杂度。不论输入的大小，所需的额外空间都是固定的。

综上所述，该算法的时间复杂度为O(1)，空间复杂度为O(1)。

LeetCode运行结果：

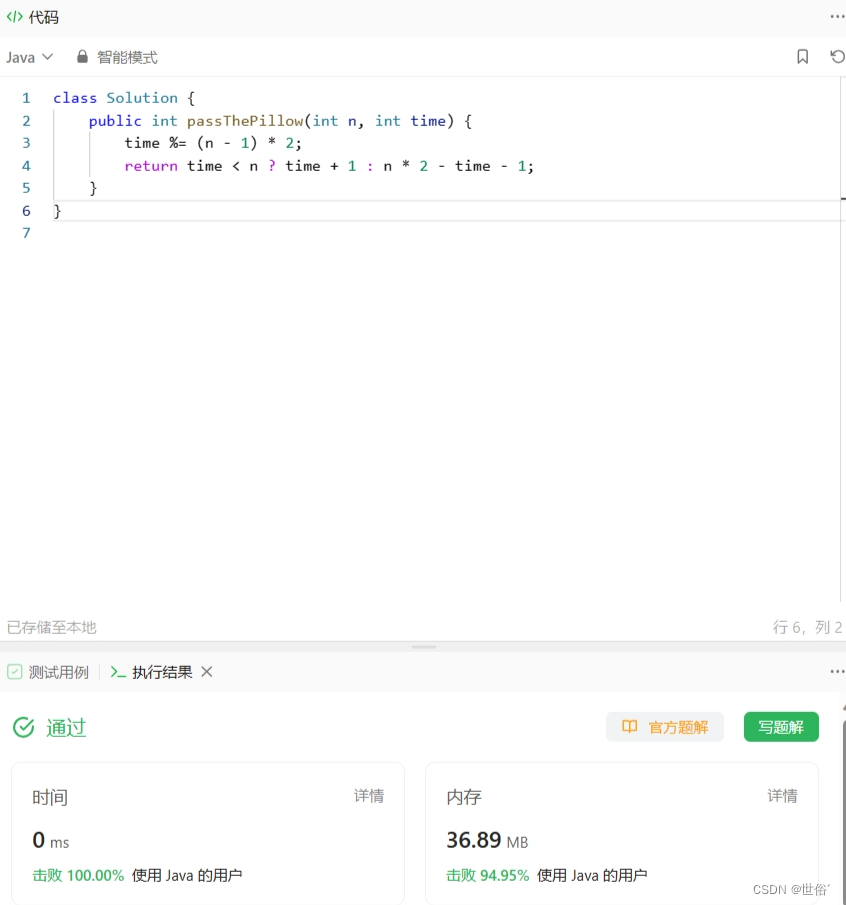
方法三：循环模拟

这个算法的思路是使用一个循环来模拟枕头传递过程，每次选择下一个接收枕头的人的位置。

1. 首先，我们初始化两个变量ans和k，分别表示当前枕头所在的位置和传递的方向。初始时，枕头在位置1，传递方向为向右。
2. 然后，我们进入一个循环，循环执行time次。在每一次循环中，首先将ans的值增加k，以选取下一个接收枕头的位置（如果k为1，则向右移动一位；如果k为-1，则向左移动一位）。然后，如果ans等于1或者等于n，表示枕头到达队伍的一端，需要改变传递方向，即将k乘以-1。
3. 重复上述步骤，直到循环执行完time次，最后返回ans即为最终枕头所在的位置编号。

class Solution {public int passThePillow(int n, int time) {int ans = 1, k = 1;while (time-- > 0) {ans += k;if (ans == 1 || ans == n) {k *= -1;}}return ans;}
}

复杂度分析：

• 时间复杂度分析：在这个算法中，循环执行time次，因此时间复杂度为O(time)。虽然time是一个变量，但是在实际应用中，time一般是一个较小的固定值。
• 空间复杂度分析：该算法只使用了几个整型变量，不随输入规模变化，因此空间复杂度为O(1)，即常数空间复杂度。

综上所述，该算法的时间复杂度为O(time)，空间复杂度为O(1)。

LeetCode运行结果：

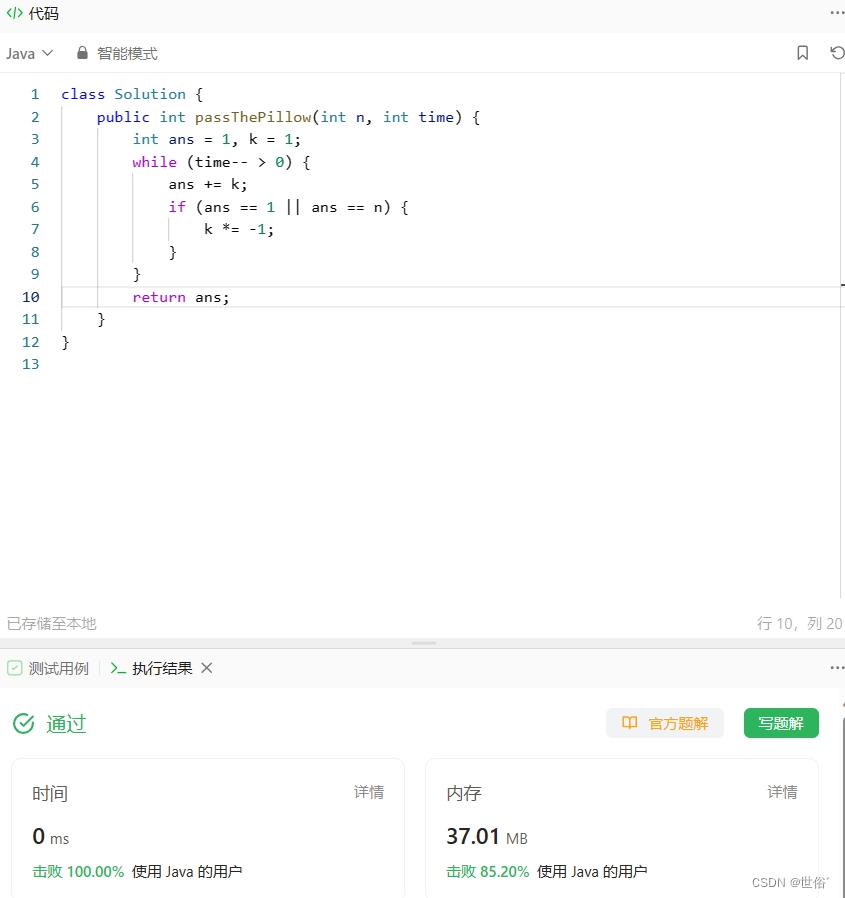
方法四：传递

这个算法的思路是，先计算出枕头到达队伍的另一端需要经过几次传递，然后根据剩余传递次数和当前位置计算最终位置。

• 首先，我们可以注意到，在N个人的队伍中，每当枕头到达队伍的某一端，就会经过N-1个人的传递。也就是说，每N-1个传递为一个周期，枕头在经过一个周期后，就会回到原来的位置并改变传递方向。因此，我们可以先计算出枕头要经过几个周期才能到达队伍的另一端。
• 接着，我们将time除以n-1得到k，表示枕头需要经过k个周期。然后，对n-1取模得到mod，表示枕头在进行完k个周期后还要经过mod次传递。
• 最后，我们根据当前位置和剩余传递次数计算最终位置。如果经过k个周期后，枕头处于队伍的左侧（即k为偶数），则最终位置为当前位置加上mod；否则，最终位置为n-mod（反向传递）。

class Solution {public int passThePillow(int n, int time) {int k = time / (n - 1);int mod = time % (n - 1);return (k & 1) == 1 ? n - mod : mod + 1;}
}

复杂度分析：

• 时间复杂度分析：在这个算法中，我们只进行了几次简单的整数运算，因此时间复杂度为O(1)，即常数时间复杂度。
• 空间复杂度分析：该算法只使用了几个整型变量，不随输入规模变化，因此空间复杂度为O(1)，即常数空间复杂度。

综上所述，该算法的时间复杂度为O(1)，空间复杂度为O(1)。

LeetCode运行结果：

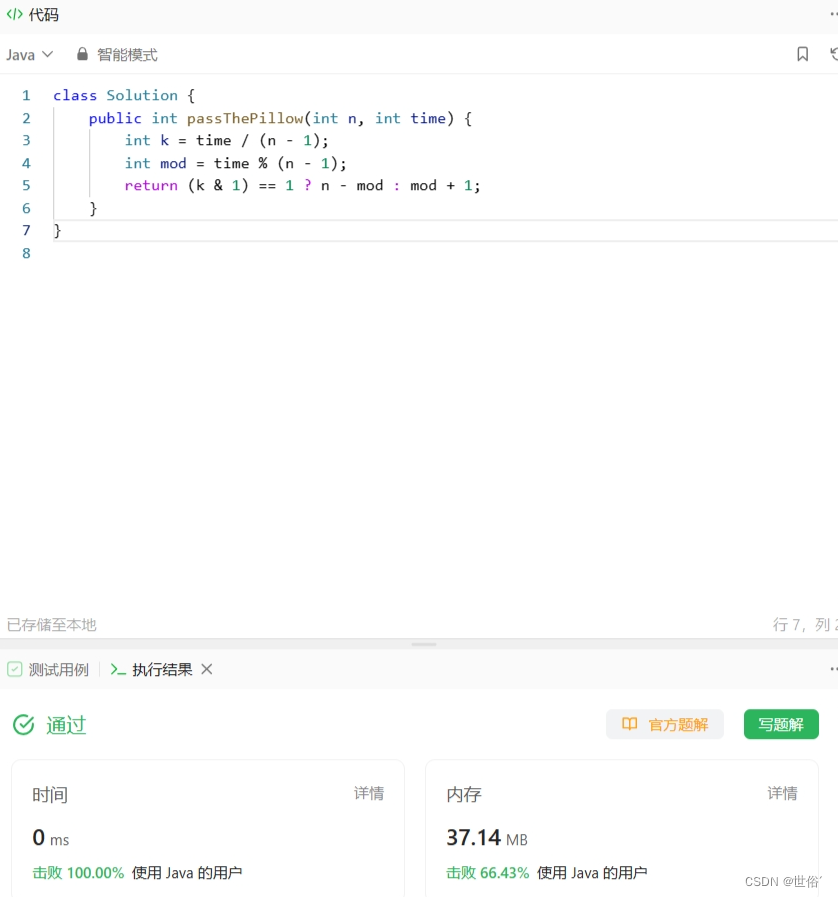
第二题

题目来源

37. 解数独 - 力扣（LeetCode）

题目内容

解决方法

方法一：回溯

这道题可以通过回溯算法来解决。回溯算法是一种暴力搜索的算法，它尝试在数独的空格中填入数字，并检查填入是否满足数独的规则。如果满足，则继续下一个空格；如果不满足，则回退到上一个空格重新选择数字。

具体实现时，可以使用递归函数来进行回溯。递归函数的参数可以包括数独数组、当前要填入的行和列。在每个空格中，我们尝试填入数字 1-9，并检查是否满足数独的规则。如果满足，则递归调用下一个空格；如果不满足，则尝试下一个数字。直到填完所有的空格，或者找到了一个有效的解为止。

class Solution {public void solveSudoku(char[][] board) {if (board == null || board.length == 0) {return;}solve(board);}private boolean solve(char[][] board) {for (int row = 0; row < 9; row++) {for (int col = 0; col < 9; col++) {if (board[row][col] == '.') {for (char num = '1'; num <= '9'; num++) {if (isValid(board, row, col, num)) {board[row][col] = num;if (solve(board)) {return true;} else {board[row][col] = '.'; // 回溯}}}return false; // 所有数字都尝试过都不满足条件，返回false}}}return true; // 数独已填满，返回true}private boolean isValid(char[][] board, int row, int col, char num) {for (int i = 0; i < 9; i++) {if (board[i][col] == num) { // 检查列是否重复return false;}if (board[row][i] == num) { // 检查行是否重复return false;}int subBoxRow = 3 * (row / 3) + i / 3; // 检查小宫格是否重复int subBoxCol = 3 * (col / 3) + i % 3;if (board[subBoxRow][subBoxCol] == num) {return false;}}return true;}
}

复杂度分析：

时间复杂度：

• 遍历数独空格：O(81)，因为数独是固定的9x9大小，所以遍历所有的空格需要O(81)的时间复杂度。
• 递归尝试填入数字：在每个空格中，我们尝试填入1-9的数字，所以对于每个空格，尝试的次数为常数，所以总的尝试次数为O(1)。
• 判断填入的数字是否满足数独规则：在判断一个数字在行、列、3x3宫格中是否重复时，我们需要遍历相关的行、列和宫格，每次都是常数时间操作，所以总的判断时间为O(1)。 综上所述，整个数独解法的时间复杂度为O(81 * 1 * 1) = O(81)。

空间复杂度：

• 递归栈空间：递归函数的调用会使用一定的栈空间，递归的最大深度不会超过空格的数量，所以空间复杂度为O(m)，其中m是空格的数量。对于数独问题来说，空格的数量最多为81个，所以空间复杂度为O(81) = O(1)。
• 数独数组修改：原地修改数独数组，不需要使用额外空间，所以空间复杂度为O(1)。

综上所述，数独解法的总体空间复杂度为O(1)，时间复杂度为O(81)。

LeetCode运行结果：

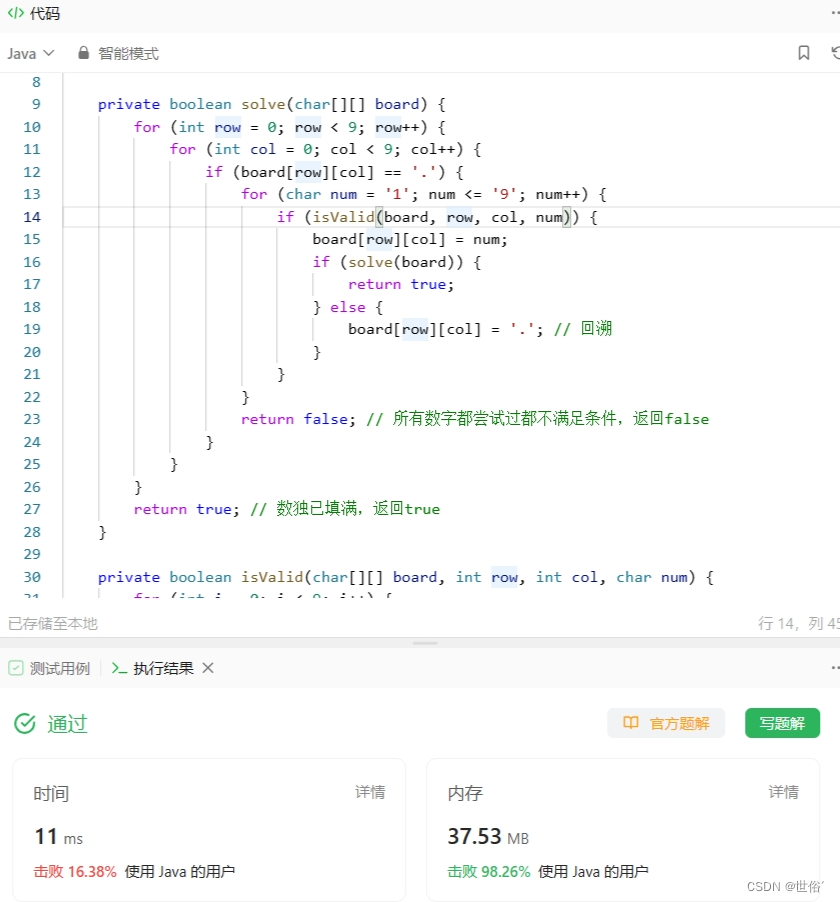
方法二：枚举优化

class Solution {private int[] line = new int[9];private int[] column = new int[9];private int[][] block = new int[3][3];private boolean valid = false;private List<int[]> spaces = new ArrayList<int[]>();public void solveSudoku(char[][] board) {for (int i = 0; i < 9; ++i) {for (int j = 0; j < 9; ++j) {if (board[i][j] != '.') {int digit = board[i][j] - '0' - 1;flip(i, j, digit);}}}while (true) {boolean modified = false;for (int i = 0; i < 9; ++i) {for (int j = 0; j < 9; ++j) {if (board[i][j] == '.') {int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;if ((mask & (mask - 1)) == 0) {int digit = Integer.bitCount(mask - 1);flip(i, j, digit);board[i][j] = (char) (digit + '0' + 1);modified = true;}}}}if (!modified) {break;}}for (int i = 0; i < 9; ++i) {for (int j = 0; j < 9; ++j) {if (board[i][j] == '.') {spaces.add(new int[]{i, j});}}}dfs(board, 0);}public void dfs(char[][] board, int pos) {if (pos == spaces.size()) {valid = true;return;}int[] space = spaces.get(pos);int i = space[0], j = space[1];int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;for (; mask != 0 && !valid; mask &= (mask - 1)) {int digitMask = mask & (-mask);int digit = Integer.bitCount(digitMask - 1);flip(i, j, digit);board[i][j] = (char) (digit + '0' + 1);dfs(board, pos + 1);flip(i, j, digit);}}public void flip(int i, int j, int digit) {line[i] ^= (1 << digit);column[j] ^= (1 << digit);block[i / 3][j / 3] ^= (1 << digit);}
}

这段代码使用了位运算和深度优先搜索来解决数独问题。下面是算法的思路：

1. 初始化 line、column 和 block 数组，用于记录每行、每列和每个九宫格中已经出现的数字状态。
2. 遍历整个数独棋盘，对于已填入数字的格子，更新相应的状态数组。
3. 使用循环，不断尝试填入数字，直到无法再填入为止。在每次循环中，遍历棋盘上的每个空白格子，并计算可填入数字的条件：
   • 通过位运算计算出当前格子可用的数字（即未出现在同一行、同一列和同一个九宫格中的数字）。
   • 如果仅有一个数字满足条件，则将其填入，并更新状态数组。
   • 如果有多个数字满足条件，则跳过该格子，继续下一个格子。
4. 遍历完成后，如果仍存在空白格子，将它们的位置保存在 spaces 列表中。
5. 调用深度优先搜索函数 dfs，递归地尝试填入空白格子：
   • 如果已经填完所有空白格子，设定 valid 为真并返回。
   • 取出下一个空白格子的位置，计算可填入的数字的条件。
   • 通过位运算，逐个尝试可填入的数字，并进行递归搜索。
6. 如果搜索到最后，仍未找到合法解，则将之前填入的数字恢复，并返回上一层继续搜索其他可能的数字组合。

这种解法通过位运算和状态压缩技巧，提高了数独求解的效率。同时使用深度优先搜索来穷举所有可能的数字组合，直到找到合法解或遍历完所有空白格子。

复杂度分析：

时间复杂度：

• 初始化部分需要遍历数独棋盘，时间复杂度为O(81) = O(1)。
• 循环填入数字的部分，最坏情况下需要进行多轮循环，但每轮循环中每个格子的操作是常数时间的，因此可以认为整体时间复杂度为O(81) = O(1)。
• 深度优先搜索部分，最坏情况下需要穷举所有可能的数字组合，并且每个格子都有9种选择，因此时间复杂度为O(9^(空白数量))。空白数量通常较小，因此可以近似看作常数，即O(1)。 综上所述，整体时间复杂度为O(1)。

空间复杂度：

• 使用了line、column和block数组来记录数字出现的状态，每个数组的长度为9，因此空间复杂度为O(9) = O(1)。
• 使用了spaces列表来保存空白格子的位置，最多有81个空白格子，因此空间复杂度为O(81) = O(1)。
• 递归调用dfs函数时产生的函数调用栈空间，最多深度为空白数量，通常较小，因此空间复杂度为O(1)。 综上所述，整体空间复杂度为O(1)。

总结起来，该算法的时间复杂度和空间复杂度都是O(1)，表示算法的运行时间和占用的额外空间都与输入规模无关，非常高效。

LeetCode运行结果：

第三题

题目来源

38. 外观数列 - 力扣（LeetCode）

题目内容

解决方法

方法一：递归

要解决这个问题，我们可以使用递归的方法来生成外观数列。首先，定义一个递归函数generateNext，该函数输入一个数字字符串，并返回对其进行描述后的新字符串。然后，我们可以使用递归调用generateNext来生成外观数列的第n项。

public class Solution {public String countAndSay(int n) {if (n == 1) {return "1";}String prev = countAndSay(n - 1);StringBuilder result = new StringBuilder();int count = 1;for (int i = 0; i < prev.length(); i++) {// 如果下一个字符与当前字符相同，则增加计数器if (i < prev.length() - 1 && prev.charAt(i) == prev.charAt(i + 1)) {count++;} else {  // 否则，将描述添加到结果中，并重置计数器result.append(count);result.append(prev.charAt(i));count = 1;}}return result.toString();}
}

在上面的代码中，当n为1时，直接返回"1"；否则，先递归调用countAndSay(n - 1)来得到前一项的描述字符串，然后遍历该字符串，统计相邻相同字符的个数，并将个数和字符添加到结果中。最后，返回结果字符串。通过调用countAndSay函数，可以得到外观数列的第n项。

复杂度分析：

• 时间复杂度分析：
• 对于每一项n，我们需要递归调用`countAndSay(n - 1)`来得到前一项的描述字符串。因此，总共需要进行n次递归调用。
• 在每一次递归调用中，我们需要遍历前一项的描述字符串，计算相邻相同字符的个数，并将结果添加到结果中。这一步的时间复杂度是O(len(prev))，其中len(prev)表示前一项描述字符串的长度。
• 综上所述，总的时间复杂度是O(1 + 2 + 3 + ... + n) = O(n^2)，其中n是给定的正整数。

空间复杂度分析：

• 递归调用`countAndSay(n)`的最大深度是n，因此递归栈的空间复杂度是O(n)。
• 此外，在每一次递归调用中，我们使用一个StringBuilder来构建当前项的描述字符串，并返回它。这个StringBuilder的空间也是O(n)。
• 综上所述，总的空间复杂度是O(n)。

综合起来，该算法的时间复杂度是O(n^2)，空间复杂度是O(n)。

LeetCode运行结果：

方法二：迭代

除了递归之外，我们还可以使用迭代的方法来生成外观数列。

public class Solution {public String countAndSay(int n) {String result = "1";for (int i = 2; i <= n; i++) {StringBuilder temp = new StringBuilder();int count = 1;for (int j = 0; j < result.length(); j++) {// 如果下一个字符与当前字符相同，则增加计数器if (j < result.length() - 1 && result.charAt(j) == result.charAt(j + 1)) {count++;} else {  // 否则，将描述添加到临时字符串中，并重置计数器temp.append(count);temp.append(result.charAt(j));count = 1;}}result = temp.toString();}return result;}
}

在上面的代码中，我们使用一个循环从2到n，依次生成外观数列的每一项。对于每一项，我们使用一个临时的StringBuilder来构建它的描述字符串，并更新result变量为临时字符串的值。

复杂度分析：

这种迭代方法的时间复杂度和空间复杂度与递归方法相同，都是O(n^2)和O(n)，因为我们仍然需要遍历前一项的描述字符串来计算当前项的描述字符串。只是在实现上，迭代方法更简单直观，没有递归的函数调用开销。

LeetCode运行结果：

方法三：动态规划

除了递归和迭代，还可以使用动态规划的方法来生成外观数列。动态规划通过存储中间结果来避免重复计算，提高效率。

public class Solution {public String countAndSay(int n) {List<String> dp = new ArrayList<>();dp.add("1"); // 初始项for (int i = 1; i < n; i++) {String prev = dp.get(i - 1); // 前一项的描述字符串StringBuilder current = new StringBuilder();int count = 1;for (int j = 0; j < prev.length(); j++) {// 如果下一个字符与当前字符相同，则增加计数器if (j < prev.length() - 1 && prev.charAt(j) == prev.charAt(j + 1)) {count++;} else {  // 否则，将描述添加到临时字符串中，并重置计数器current.append(count);current.append(prev.charAt(j));count = 1;}}dp.add(current.toString()); // 将当前项的描述字符串添加到动态规划数组中}return dp.get(n - 1); // 返回第n项的描述字符串}
}

在上面的代码中，我们使用一个动态规划数组dp来存储每一项的描述字符串。初始时，将"1"作为第一项的描述字符串。然后，从2到n依次计算每一项的描述字符串，并将其存储到动态规划数组中。最后，返回第n项的描述字符串。

复杂度分析：

使用动态规划方法，我们将外观数列的每一项的描述字符串存储起来，避免了重复计算，提高了效率。它的时间复杂度仍然是O(n^2)，但相对于递归和迭代方法，动态规划在计算过程中节省了一些中间计算的时间。空间复杂度为O(n)，用来存储动态规划数组。

LeetCode运行结果：

方法四：递推

除了前面提到的方法，还可以使用递推方法来生成外观数列。递推方法是指根据已知的前几项，通过递推公式计算得到后续的项数。

public class Solution {public String countAndSay(int n) {String current = "1"; // 初始项for (int i = 1; i < n; i++) {StringBuilder next = new StringBuilder();int count = 1;char ch = current.charAt(0);for (int j = 1; j < current.length(); j++) {// 如果下一个字符与当前字符相同，则增加计数器if (current.charAt(j) == ch) {count++;} else { // 否则，将计数器和当前字符追加到下一个描述字符串中，并更新当前字符和计数器next.append(count).append(ch);ch = current.charAt(j);count = 1;}}next.append(count).append(ch); // 将最后一个连续数字段追加到下一个描述字符串中current = next.toString(); // 更新当前描述字符串为下一个描述字符串}return current; // 返回第n项的描述字符串}
}

在这种方法中，我们根据外观数列的定义，通过递推公式计算每一项的描述字符串。具体来说，我们遍历当前项的描述字符串，记录当前字符和计数器。如果下一个字符与当前字符相同，则增加计数器；否则，将计数器和当前字符追加到下一个描述字符串中，并更新当前字符和计数器。最后，将最后一个连续数字段追加到下一个描述字符串中，更新当前描述字符串为下一个描述字符串。通过这种方式，我们可以递推得到所有项的描述字符串。

复杂度分析：

• 使用递推方法，我们避免了使用递归或动态规划来求解外观数列，减少了时间和空间复杂度。但是，递推方法需要根据递推公式，对每一项进行计算，因此时间复杂度仍然为O(n^2)。
• 空间复杂度为O(m)，其中m是当前项的长度。在每次计算下一项时，我们只需使用一个StringBuilder对象来构建描述字符串，其长度为m。每次计算完成后，我们无需保留之前的计算结果，因此只需要恒定的额外空间来存储当前项的描述字符串。因此，总的空间复杂度为O(m)。

LeetCode运行结果：