优先级队列 一端进,另一端出 按优先级出队
普通队列 一端进,另一端出 FIFO
我们做个约定:数字大的,优先级越高 ,优先出队
无序数组实现
要点
入队保持顺序
出队前找到优先级最高的出队,相当于一次选择排序
public class PriorityQueue1<E extends Priority> implements Queue<E> {Priority[] array;int size;public PriorityQueue1(int capacity) {array = new Priority[capacity];}@Override // O(1)public boolean offer(E e) {if (isFull()) {return false;}array[size++] = e;return true;}// 返回优先级最高的索引值private int selectMax() {int max = 0;for (int i = 1; i < size; i++) {if (array[i].priority() > array[max].priority()) {max = i;}}return max;}@Override // O(n)public E poll() {if (isEmpty()) {return null;}int max = selectMax();E e = (E) array[max];remove(max);return e;}//这里的删除操作有两种:一、如果是最大索引上的元素要被删除,则只需要将数组大小-1即可//二、如果不是最大索引上的元素要被删除,则要从要被删除的索引后面的数字集体向前移动private void remove(int index) {if (index < size - 1) { //说明不是最后一个元素System.arraycopy(array, index + 1,array, index, size - 1 - index);}array[--size] = null; // help GC}@Overridepublic E peek() {if (isEmpty()) {return null;}int max = selectMax();return (E) array[max];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == array.length;}
}测试用例:
@Testpublic void poll() {PriorityQueue1<Entry> queue = new PriorityQueue1<>(5);queue.offer(new Entry("task1", 4));queue.offer(new Entry("task2", 3));queue.offer(new Entry("task3", 2));queue.offer(new Entry("task4", 5));queue.offer(new Entry("task5", 1));assertFalse(queue.offer(new Entry("task6", 7)));System.out.println(Arrays.toString(queue.array));assertEquals(5, queue.poll().priority());System.out.println(Arrays.toString(queue.array));assertEquals(4, queue.poll().priority());assertEquals(3, queue.poll().priority());assertEquals(2, queue.poll().priority());assertEquals(1, queue.poll().priority());
}有序数组实现
实现方法与无序数组恰恰相反,对于poll操作很简单,但是在offer操作时要实现的就是插入排序的算法
要点
入队后排好序,优先级最高的排列在尾部
出队只需删除尾部元素即可
public class PriorityQueue2<E extends Priority> implements Queue<E> {Priority[] array;int size;public PriorityQueue2(int capacity) {array = new Priority[capacity];}// O(n)@Overridepublic boolean offer(E e) {if (isFull()) {return false;}insert(e);size++;return true;}// 一轮插入排序private void insert(E e) {int i = size - 1;//循环条件:1.遍历到低就退出 2.当遍历到第一次比自己低的索引时就退出while (i >= 0 && array[i].priority() > e.priority()) {//将优先级比搜索值要小都向上移动array[i + 1] = array[i];i--;}array[i + 1] = e;}// O(1)@Overridepublic E poll() {if (isEmpty()) {return null;}E e = (E) array[size - 1];array[--size] = null; // help GCreturn e;}@Overridepublic E peek() {if (isEmpty()) {return null;}return (E) array[size - 1];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == array.length;}
}测试用例:
@Testpublic void poll() {PriorityQueue2<Entry> queue = new PriorityQueue2<>(5);queue.offer(new Entry("task1", 4));queue.offer(new Entry("task2", 3));queue.offer(new Entry("task3", 2));queue.offer(new Entry("task4", 5));queue.offer(new Entry("task5", 1));assertFalse(queue.offer(new Entry("task6", 7)));assertEquals("task4", queue.peek().value);assertEquals("task4", queue.poll().value);assertEquals("task1", queue.poll().value);assertEquals("task2", queue.poll().value);assertEquals("task3", queue.poll().value);assertEquals("task5", queue.poll().value);
}堆实现
计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。
什么叫完全二叉树?
答:
1.除了最后一层不用满足有两个分支,其他层都要满足有两个分支
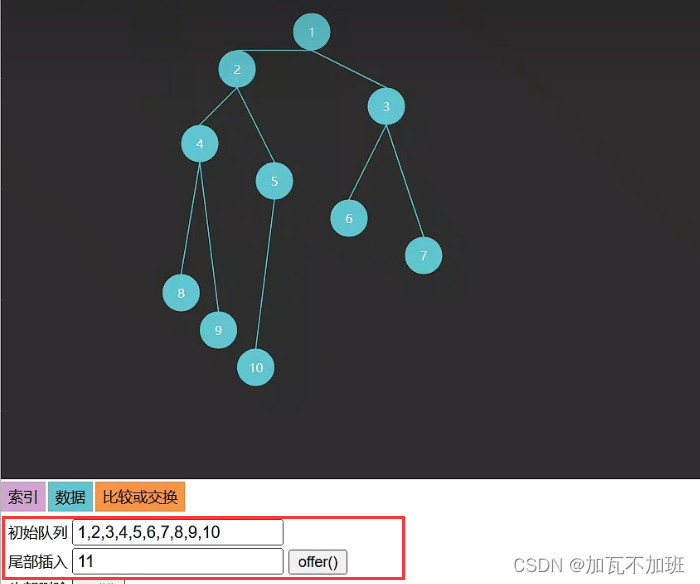
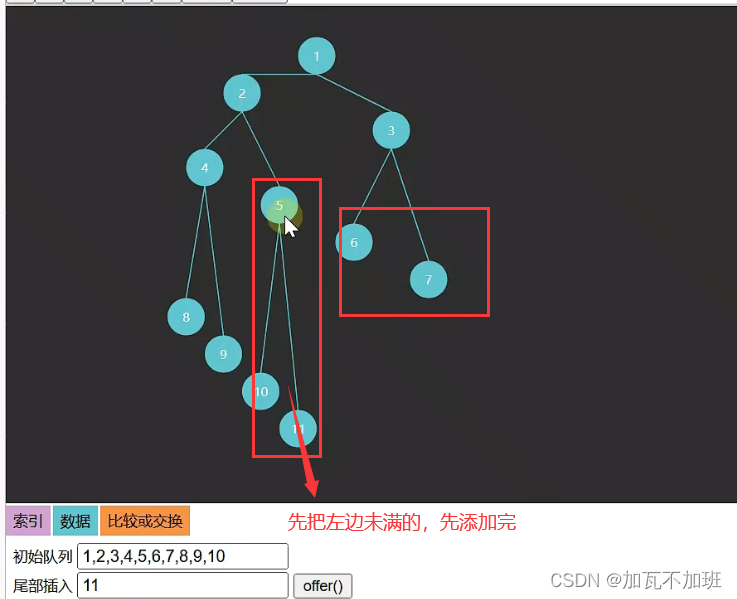
2.如果再往完全二叉树中加一个节点,那么必须靠左添加,从左往右依次填满,左边没有填满之前,右边就不能填,如图:
添加前:
添加后:
堆的特性如下:堆分为两种:大顶堆与小顶堆
在大顶堆中,任意节点 C 与它的父节点 P 符合 P.value >= C.value:父节点的值>=子节点的值
而小顶堆中,任意节点 C 与它的父节点 P 符合 P.value <= C.value:父节点的值<=子节点的值
最顶层的节点(没有父亲)称之为 root 根节点
例1 - 满二叉树(Full Binary Tree)特点:每一层都是填满的

例2 - 完全二叉树(Complete Binary Tree)特点:最后一层可能未填满,靠左对齐
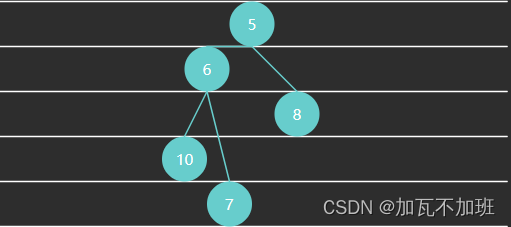
例3 - 大顶堆
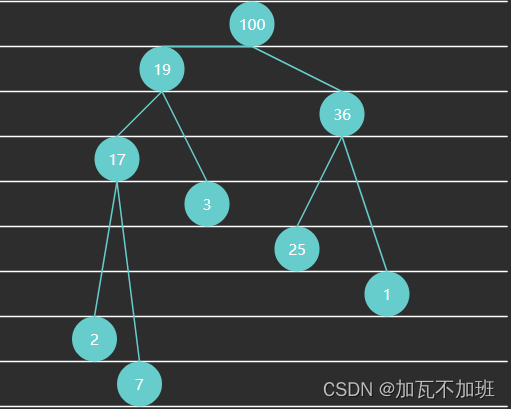
例4 - 小顶堆
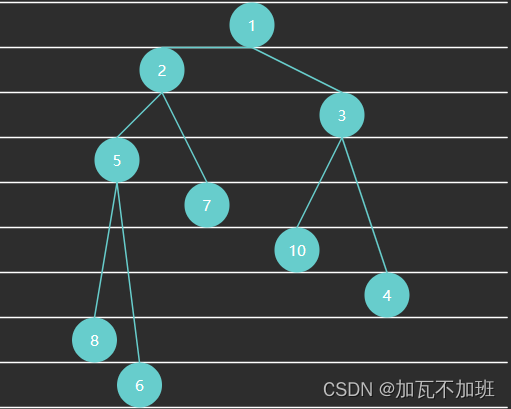
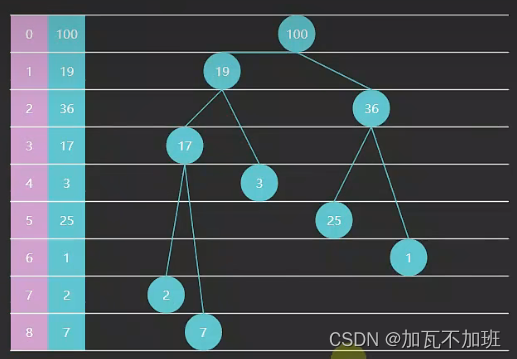
完全二叉树可以使用数组来表示:
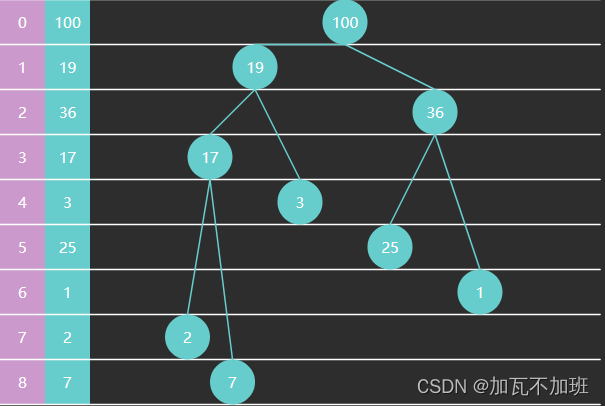
那完全二叉树显然是个非线性的数据结构,但是它存储的时候可以使用线性的数组结构来存储数据:
特征
如果从索引 0 开始存储节点数据
节点 i 的父节点为 floor((i-1)/2),当 i>0 时
节点 i 的左子节点为 2i+1,右子节点为 2i+2,当然它们得 < size
如果从索引 1 开始存储节点数据
节点 i 的父节点为 floor(i/2),当 i > 1 时
节点 i 的左子节点为 2i,右子节点为 2i+1,同样得 < size
代码:
//利用大顶堆来实现 从索引 0 开始存储节点数据
public class PriorityQueue4<E extends Priority> implements Queue<E> {Priority[] array;int size;public PriorityQueue4(int capacity) {array = new Priority[capacity];}@Override//1.添加元素的时候,要符合条件,从左往右依次填满//2.根据规律,我们填的元素一定是在数组中最后一位添加//3.找填加元素的父类利用公式:节点 i 的父节点为 floor((i-1)/2),当 i>0 时//4.当添加的子元素值大于父类的元素值则要将父类的元素值与添加的子元素值进行交换,然后再让添加的子元素值再与上一级父类的元素值进行比较//简单来说://1. 入堆新元素, 加入到数组末尾 (索引位置 child)//2. 不断比较新加元素与它父节点(parent)优先级 (上浮)// - 如果父节点优先级低, 则向下移动, 并找到下一个 parent// - 直至父节点优先级更高或 child==0 为止public boolean offer(E offered) {if (isFull()) {return false;}int child = size++;int parent = (child - 1) / 2;while (child > 0 && offered.priority() > array[parent].priority()) {array[child] = array[parent];child = parent;//java整数取整就是向下取整 所以不需要调用floor函数parent = (child - 1) / 2;}array[child] = offered;return true;}//交换堆顶和尾部元素private void swap(int i, int j) {Priority t = array[i];array[i] = array[j];array[j] = t;}@Override//移除优先级最高的元素/*1. 交换堆顶和尾部元素, 让尾部元素出队2. (下潜)- 从堆顶开始, 将父元素与两个孩子较大者交换- 直到父元素大于两个孩子, 或没有孩子为止*/public E poll() {if (isEmpty()) {return null;}// 1. 交换堆顶和尾部元素swap(0, size - 1);//让尾部元素出队size--;Priority e = array[size];array[size] = null;shiftDown(0); return (E) e;}//2. (下潜)// - 从堆顶开始, 将父元素与两个孩子较大者交换// - 直到父元素大于两个孩子, 或没有孩子为止void shiftDown(int parent) {//节点 i 的左子节点为 2i+1,右子节点为 2i+2,当然它们得 < sizeint left = 2 * parent + 1;int right = left + 1;int max = parent;//假设父元素优先级最高if (left < size && array[left].priority() > array[max].priority()) {max = left;}if (right < size && array[right].priority() > array[max].priority()) {max = right;}if (max != parent) {//有孩子比父亲大swap(max, parent);shiftDown(max);}}@Overridepublic E peek() {if (isEmpty()) {return null;}return (E) array[0];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == array.length;}
}参考代码:GitHub - 1693905917/DataStructure: 数据结构与算法