什么是递归
函数自己调用自己的情况。
为什么要用递归
主问题->子问题 子问题->子问题
宏观看待递归
不要在意细节展开图,把函数当成一个黑盒,相信这个黑盒一定能完成任务。
如何写好递归
一、汉诺塔
class Solution {
public:void dfs(vector<int>& A,vector<int>& B,vector<int>& C,int n){if(n == 1) {C.push_back(A.back());A.pop_back();return;};dfs(A,C,B,n-1);C.push_back(A.back());A.pop_back();dfs(B,A,C,n-1);}void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {dfs(A,B,C,A.size());}
}; 二、合并两个有序链表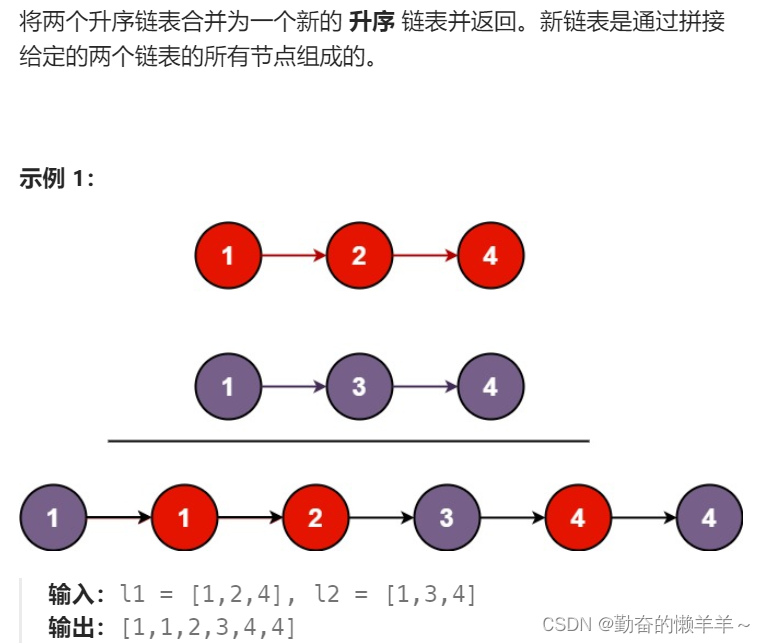

/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {if(l1 == nullptr)return l2;if(l2 == nullptr) return l1;if(l1->val <= l2->val) {l1->next = mergeTwoLists(l1->next,l2);return l1;}else{l2->next = mergeTwoLists(l1,l2->next);return l2;}}
}; 
三、反转链表

class Solution {
public:ListNode* reverseList(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;ListNode* newhead = reverseList(head->next);head->next->next = head;head->next = nullptr;return newhead;}
};四、两两交换链表中的结点
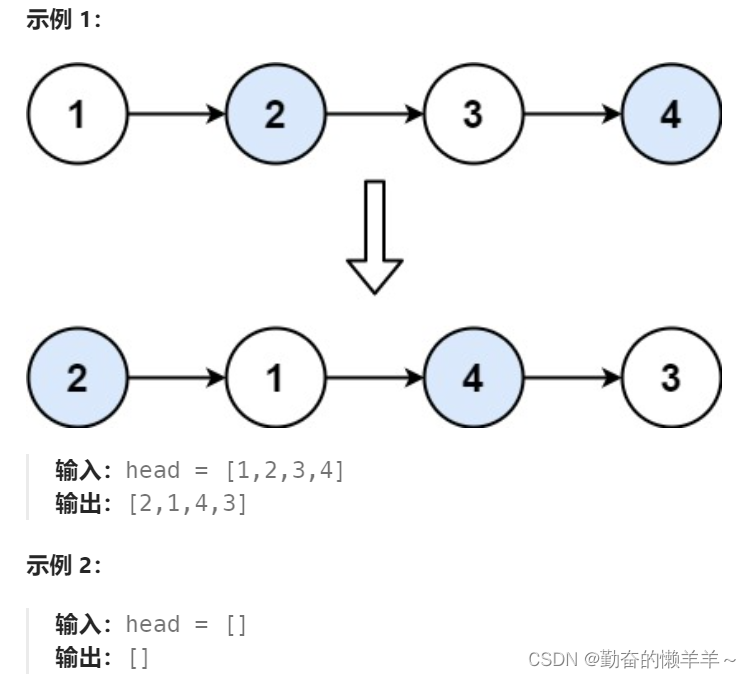
分析跟上一题差不多,不详解。
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;ListNode*newhead = swapPairs(head->next->next);auto ret = head->next; head->next->next = head;head->next = newhead;return ret;}五、快速幂
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,x^n )。



class Solution {
public:double pow(double x,long long n){if(n == 0)return 1.0;double tmp = pow(x,n/2);return n%2 == 0? tmp*tmp:tmp*tmp*x; }double myPow(double x, int n) {if(n < 0) return 1.0/(pow(x,-(long long)n));return pow(x,n);}
};