个人主页：兜里有颗棉花糖
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时，记录一下自己的学习过程，希望对大家有所帮助
🍓希望我们一起努力、成长，共同进步。

点击直接跳转到该题目

1️⃣题目描述

假如有一排房子，共 n 个，每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。

当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。

例如，costs[0][0] 表示第 0 号房子粉刷成红色的成本花费；costs[1][2] 表示第 1 号房子粉刷成绿色的花费，以此类推。

请计算出粉刷完所有房子最少的花费成本。

示例1：

输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色，1 号房子粉刷成绿色，2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。

示例2：

输入: costs = [[7,6,2]]
输出: 2

注意事项：

• costs.length == n
• costs[i].length == 3
• 1 <= n <= 100
• 1 <= costs[i][j] <= 20

2️⃣题目解析

这里我们定义一个大小为（n + 1）* 3的二维dp表，之所以是n + 1是为了解决dp表的初始化问题（多出来的那个1我们可以将其理解为一个虚拟节点），具体解释如下：

• 为什么要使用大小为 (n+1) x 3 的数组呢？这是因为我们希望使用 dp[0] 表示第 0 个房屋（即没有房屋）的情况，而不是从 dp[1] 开始表示第一个房屋的情况。为了方便地处理边界情况，我们可以将数组的大小设置为 (n+1) x 3，从而在 dp[1] ~ dp[n] 中存储每个房屋对应的最小成本，而 dp[0] 可以被初始化为全0。

dp[i][0] 表示涂到第 i 房屋时，将其涂成红颜色的最小成本。
dp[i][1] 表示涂到第 i 房屋时，将其涂成蓝颜色的最小成本。
dp[i][2] 表示涂到第 i 房屋时，将其涂成绿颜色的最小成本。

状态转移方程如下：

• dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + costs[i - 1][0]
• dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + costs[i - 1][1]
• dp[i][2] = min(dp[i-1][0],dp[i-1][1]) + costs[i - 1][2]

3️⃣解题代码

class Solution {
public:int minCost(vector<vector<int>>& costs) {int n = costs.size();vector<vector<int>> dp(n+1,vector<int>(3));for(int i = 1;i <= n;i++){dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + costs[i-1][0];dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + costs[i-1][1];dp[i][2] = min(dp[i-1][0],dp[i-1][1]) + costs[i-1][2];}return min(dp[n][0],min(dp[n][1],dp[n][2]));}
};

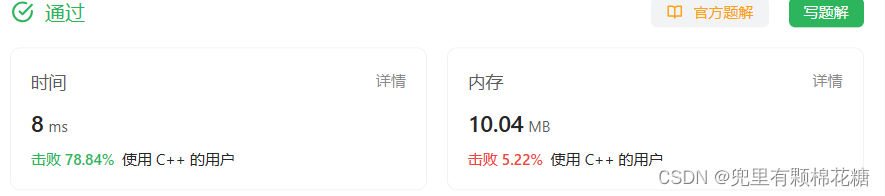
通过啦：