1. 题目

        在股票交易中，如果前一天的股价高于后一天的股价，则可以认为存在一个「交易逆序对」。请设计一个程序，输入一段时间内的股票交易记录 record，返回其中存在的「交易逆序对」总数。

2. 输入输出样例

        示例1

输入：record = [9, 7, 5, 4, 6]
输出：8
解释：交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。

        限制

0 <= record.length <= 50000

3. 实现思路

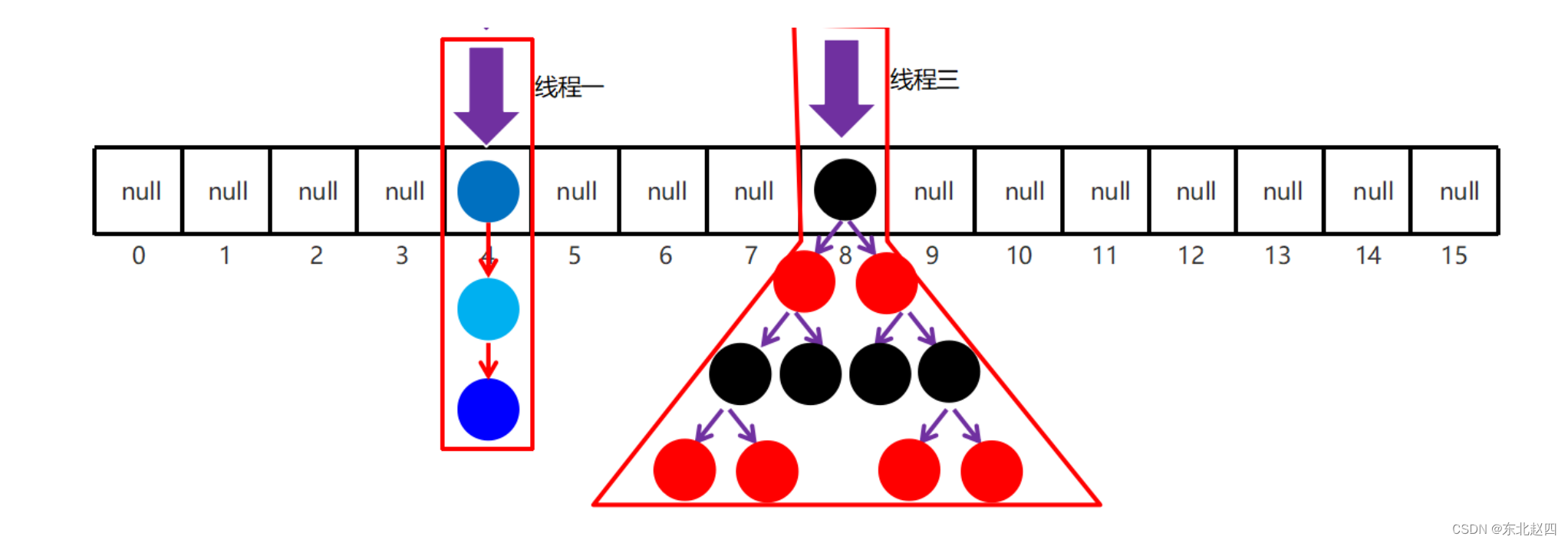
         使用分治和归并排序的方法来计算整数数组中的逆序对数量，主要的思路是：

        （1）将数组分解为两个子数组；

        （2）递归地计算每个子数组的逆序对数量；

        （3）在归并的过程中，统计两个子数组之间的逆序对数量，并将子数组合并成一个有序的数组；

        （4）通过递归和归并的结合，得出整个数组中的逆序对数量。

• 分解阶段：将数组分解为两个子数组，这个过程需要 O(1) 的时间。
• 递归计算阶段：递归地计算左子数组和右子数组的逆序对数量，每次递归都将数组大小减半。因为有 log₂(n) 层递归，每层的时间复杂度是 O(n)，所以总的时间复杂度是 O(nlogn)。
• 归并阶段：在归并的过程中，需要线性时间 O(n) 来合并两个有序子数组。因为在每层递归中都会执行这个操作，总的时间复杂度是 O(nlogn)。
•  综合以上三个阶段，总的时间复杂度是 O(nlogn)。

4. 实现代码 

// 定义递归函数 nxs，用于计算逆序对数量
int nxs(int* nums, int l, int r){// 如果子数组的左边界大于或等于右边界，说明子数组中没有元素或只有一个元素，逆序对数量为0if(l >= r){return 0;}// 分解：将当前数组划分为两个子数组int mid = (l + r) / 2;int tl = nxs(nums, l, mid); // 递归计算左子数组中的逆序对数量int tr = nxs(nums, mid + 1, r); // 递归计算右子数组中的逆序对数量// 求和（采用归并排序的思想）int i = l, j = mid + 1, k = 0, count = 0;int *B = (int*)malloc(sizeof(int) * (r - l + 1)); // 创建一个临时数组 B 存储归并后的结果// 归并过程while(i <= mid && j <= r){if(nums[i] > nums[j]){B[k++] = nums[j++];count += (mid - i + 1); // 如果 nums[i] > nums[j]，则说明 nums[i] 及其后面的元素都与 nums[j] 构成逆序对}else{B[k++] = nums[i++];}}// 处理剩余元素while(i <= mid){B[k++] = nums[i++];}while(j <= r){B[k++] = nums[j++];}// 将归并后的结果复制回原数组 numsi = l, j = 0;while(j < k){nums[i++] = B[j++];}// 返回当前子数组中的逆序对数量return tl + count + tr;
}// 主函数，调用 nxs 函数来计算整个数组中的逆序对数量
int reversePairs(int* nums, int numsSize){return nxs(nums, 0, numsSize - 1);
}

LCR 170. 交易逆序对的总数 - 力扣（LeetCode）https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/