目录
框架:排列/组合/子集
元素无重不可复选
全排列
子集
组合:[1, n] 中的 k 个数
分割成回文串
元素无重不可复选:排序,多条值相同的只遍历第一条
子集/组合
先进行排序,让相同的元素靠在一起,如果发现 nums[i] == nums[i-1],则跳过
排列
元素无重可复选
子集/组合:sum=target
排列:去除 used 剪枝
N皇后
如果不能成功,那么返回的时候我们就还要把这个位置还原。这就是回溯算法,也是试探算法。
解决一个回溯问题,实际上就是一个决策树的遍历过程。
1、路径:已选择。
2、选择列表:可选择。
3、结束条件:无选择。
框架:排列/组合/子集
result = []
function backtrack(路径, 选择列表):if 满足结束条件:result.add(路径)result.push([...path])或者result.push(path.slice())//path还会改变,所以不能传引用地址returnfor 选择 in 选择列表:做选择pushbacktrack(路径, 选择列表)撤销选择pop数组(有一定的剪枝,不用判断是否use)
const backtrack = (start) => {// 回溯算法标准框架for (let i = start; i < nums.length; i++) {// 做选择track.push(nums[i]);// 回溯遍历下一层节点backtrack(i + 1);// 撤销选择track.pop();}};backtrack(0);
图
function backtrack(nums, used, track, res) {for (let i = 0; i < nums.length; i++) {if (used[i]) {continue;}track.push(nums[i]);used[i] = true;backtrack(nums, used, track, res);track.pop();used[i] = false;}
}全排列中
做选择/撤销选择 可用if(path.includes(item)) continue;代替元素无重不可复选
全排列
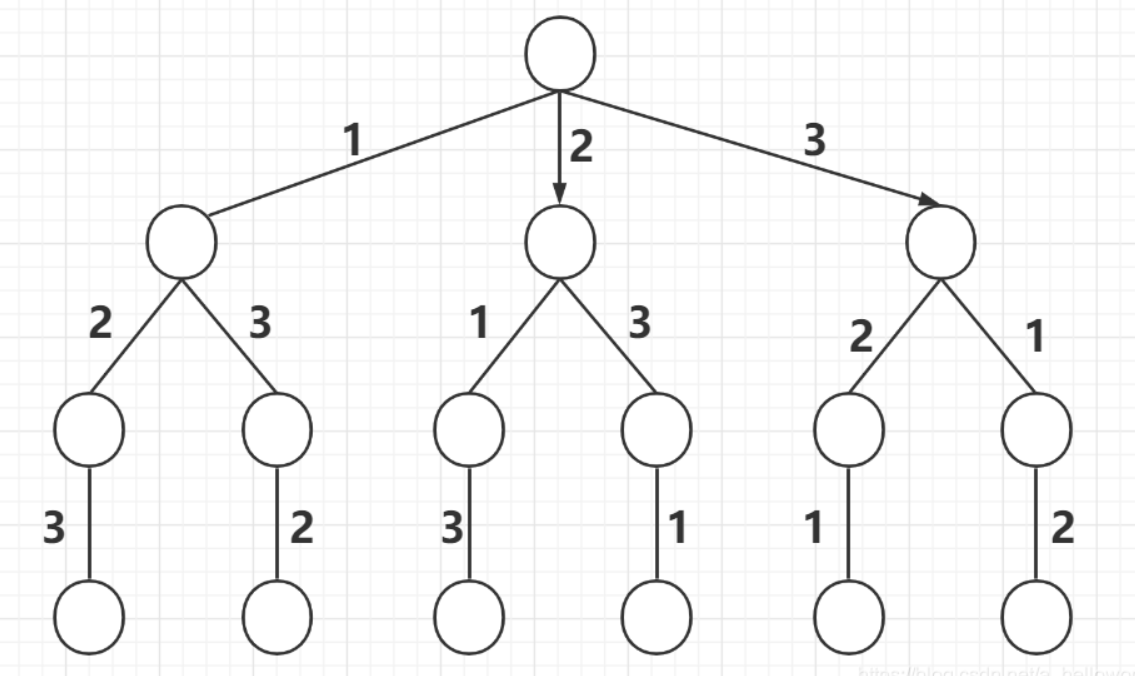
key:
- path.length == string.length
- path.includes(item)
const _permute = string => {const res = [];const backtrace = path => {if(path.length == string.length){res.push(path);return;}for(const item of string) {if(path.includes(item)) continue;backtrace(path + item);}};backtrace('');return res;
}子集
输入一个无重复元素的数组 nums,其中每个元素最多使用一次,请你返回 nums 的所有子集
比如输入 nums = [1,2,3],算法应该返回如下子集:
[ [],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3] ]

/*** @param {number[]} nums* @return {number[][]}*/
var subsets = function(nums) {// 用于存储结果const res = [];// 用于记录回溯路径const track = [];/*** 回溯算法的核心函数,用于遍历子集问题的回溯树* @param {number} start - 控制树枝的遍历,避免产生重复子集*/const backtrack = (start) => {// 前序遍历位置,每个节点的值都是一个子集res.push([...track]);// 回溯算法标准框架for (let i = start; i < nums.length; i++) {// 做选择track.push(nums[i]);// 回溯遍历下一层节点backtrack(i + 1);// 撤销选择track.pop();}};backtrack(0);return res;
};组合:[1, n] 中的 k 个数
返回范围 [1, n] 中所有可能的 k 个数的组合,剪枝
let result = []
let path = []
var combine = function(n, k) {result = []combineHelper(n, k, 1)return result
};
const combineHelper = (n, k, startIndex) => {if (path.length === k) {result.push([...path])return}for (let i = startIndex; i <= n - (k - path.length) + 1; ++i) {path.push(i)combineHelper(n, k, i + 1)path.pop()}
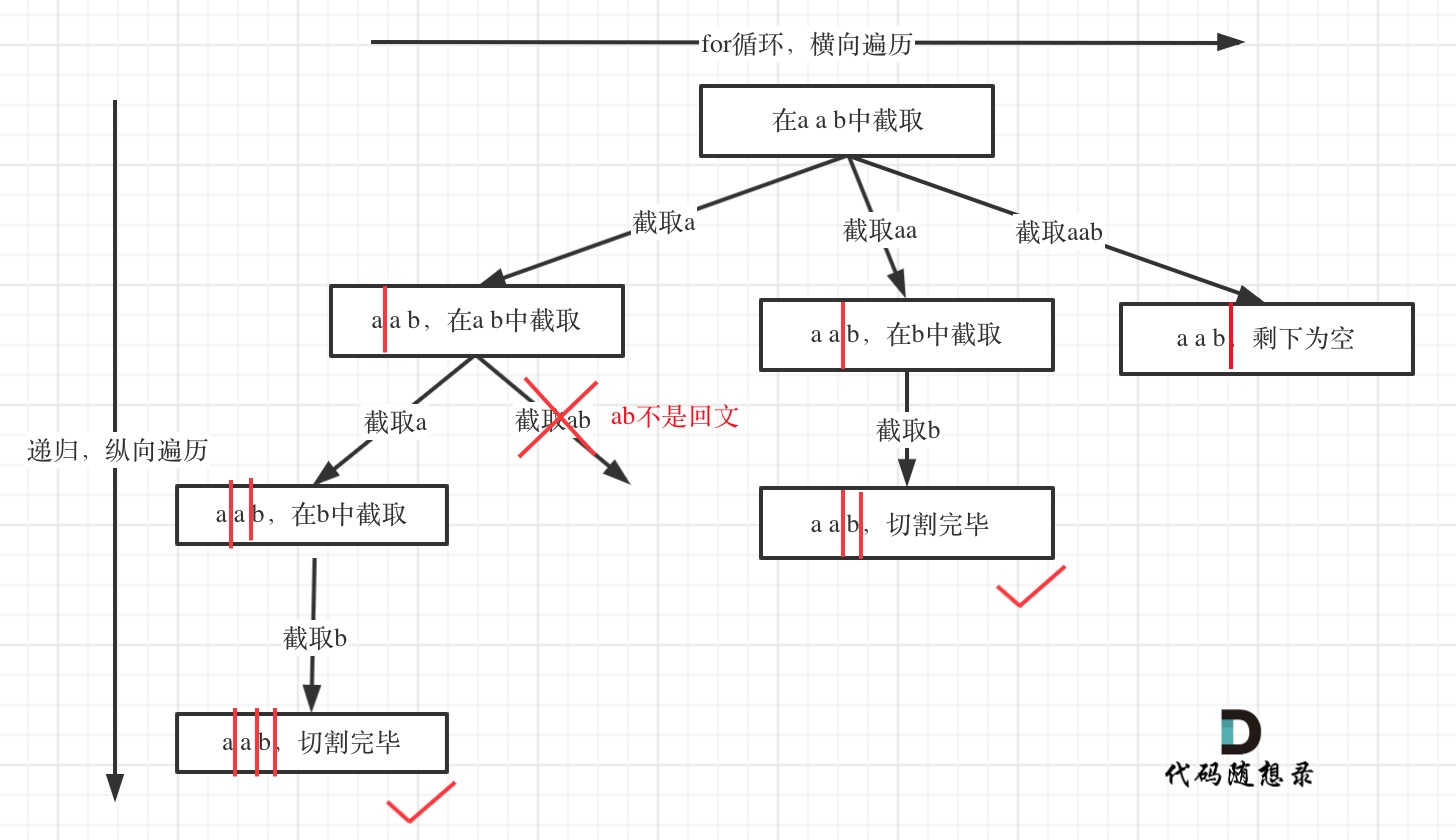
}分割成回文串
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段.....。
/*** @param {string} s* @return {string[][]}*/
const isPalindrome = (s, l, r) => {for (let i = l, j = r; i < j; i++, j--) {if(s[i] !== s[j]) return false;}return true;
}var partition = function(s) {const res = [], path = [], len = s.length;backtracking(0);return res;function backtracking(startIndex) {if(startIndex >= len) {res.push(Array.from(path));return;}for(let i = startIndex; i < len; i++) {if(!isPalindrome(s, startIndex, i)) continue;path.push(s.slice(startIndex, i + 1));backtracking(i + 1);path.pop();}}
};元素无重不可复选:排序,多条值相同的只遍历第一条
子集/组合
nums = [1,2,2],你应该输出:
[ [],[1],[2],[1,2],[2,2],[1,2,2] ]如果一个节点有多条值相同的树枝相邻,则只遍历第一条,剩下的都剪掉,不要去遍历:
先进行排序,让相同的元素靠在一起,如果发现 nums[i] == nums[i-1],则跳过
排列
// 注意:javascript 代码由 chatGPT🤖 根据我的 java 代码翻译,旨在帮助不同背景的读者理解算法逻辑。
// 本代码还未经过力扣测试,仅供参考,如有疑惑,可以参照我写的 java 代码对比查看。/*** @param {number[]} nums* @return {number[][]}*/var permuteUnique = function(nums) {let res = [];let track = [];let used = new Array(nums.length).fill(false);// 先排序,让相同的元素靠在一起nums.sort((a, b) => a - b);backtrack(nums, used, track, res);return res;
};/*** @param {number[]} nums* @param {boolean[]} used* @param {number[]} track* @param {number[][]} res*/
function backtrack(nums, used, track, res) {if (track.length === nums.length) {res.push(track.slice());return;}for (let i = 0; i < nums.length; i++) {if (used[i]) {continue;}// 新添加的剪枝逻辑,固定相同的元素在排列中的相对位置if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) {continue;}track.push(nums[i]);used[i] = true;backtrack(nums, used, track, res);track.pop();used[i] = false;}
}
元素无重可复选
子集/组合:sum=target
想让每个元素被重复使用,我只要把 i + 1 改成 i 即可
给之前的回溯树添加了一条树枝,在遍历这棵树的过程中,一个元素可以被无限次使用
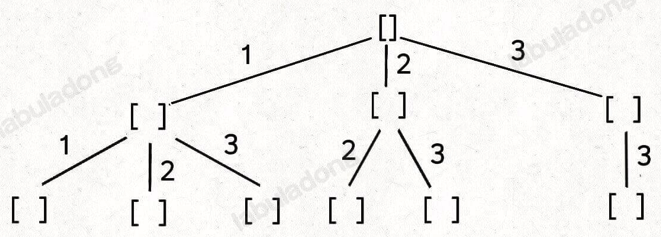
这棵回溯树会永远生长下去,所以我们的递归函数需要设置合适的 base case 以结束算法,即路径和大于 target 时就没必要再遍历下去了
排列:去除 used 剪枝
N皇后
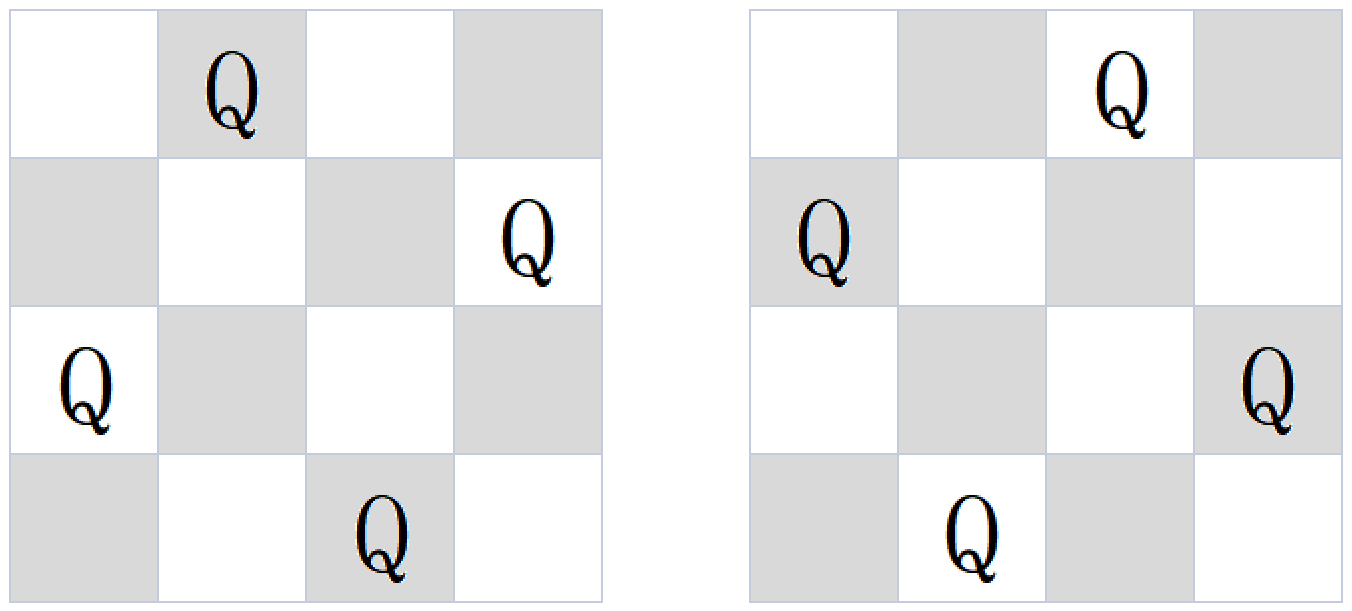
在 n * n 的棋盘上要摆 n 个皇后,
要求:任何两个皇后不同行,不同列也不在同一条斜线上,
求给一个整数 n ,返回 n 皇后的摆法数。
要求:空间复杂度 O(1) ,时间复杂度O(n!)
- 要确定皇后的位置,其实就是确定列的位置,因为行已经固定了
- 进一步讲,也就是如何摆放 数组
arr[0,1,2,3,...,n-1] - 如果没有【不在同一条斜线上】要求,这题其实只是单纯的全排列问题
- 在全排列的基础上,根据N皇后的问题,去除一些结果
-
arr:n个皇后的列位置 -
res:n皇后排列结果 -
ruler:记录对应的列位置是否已经占用(也是是否有皇后),如果有,那么设为1,没有设为0 -
setPos:哈希集合,标记正斜线(从左上到右下)位置,如果在相同正斜线上,坐标(x,y)满足 y-x 都相同,(y1 - x1)应该等于(y2 - x2)。 -
setCon:哈希集合,标记反正斜线(从y右上到左下)位置,如果在相同反斜线上,坐标(x,y)满足 x+y 都相同,(x1 + y1)应该等于(x2 + y2)。 -
是否在同一斜线上,其实就是这两个点的所形成的斜线的斜率是否为±1。点P(a,b) ,点Q(c,d)
(1)斜率为1 (d-b)/(c-a) = 1,横纵坐标之差相等
(2)斜率为-1 (d-b)/(c-a) = -1 ,等式两边恒等变形 a+b = c + d ,横纵坐标之和相等
/**** @param n int整型 the n* @return int整型*/
function Nqueen(n) {let res = []; //二维数组,存放每行Q的列坐标let isQ = new Array(n).fill(0); //记录该列是否有Qlet setPos = new Set(); //标记正对角线let setCon = new Set(); // 标记反对角线//给当前row找一个colconst backTrace = (row, path) => {if (path.length === n) {res.push(path);return;}for (let col = 0; col < n; col++) {if (isQ[col] == 0 &&!setPos.has(row - col) &&!setCon.has(row + col)) {path.push(col);isQ[col] = 1;setPos.add(row - col);setCon.add(row + col);backTrace(row + 1, path);path.pop();isQ[col] = 0;setPos.delete(row - col);setCon.delete(row + col);}}};backTrace(0, []);return res.length;
}
module.exports = {Nqueen: Nqueen,
};
动态规划的暴力求解阶段就是回溯算法。只是有的问题具有重叠子问题性质,可以用 dp table 或者备忘录优化,将递归树大幅剪枝,这就变成了动态规划。