文心一言 VS 讯飞星火 VS chatgpt （108）-- 算法导论10.1 6题

六、用go语言，说明如何用两个栈实现一个队列，并分析相关队列操作的运行时间。

文心一言：

使用两个栈实现队列的基本思想是利用一个栈（stack1）来处理入队操作，另一个栈（stack2）来处理出队操作。以下是使用 Go 语言实现的代码：

package main  import "fmt"  type Queue struct {  stack1, stack2 []int  
}  func NewQueue() *Queue {  return &Queue{}  
}  func (q *Queue) Enqueue(x int) {  q.stack1 = append(q.stack1, x)  
}  func (q *Queue) Dequeue() int {  if len(q.stack2) == 0 {  for len(q.stack1) > 0 {  q.stack2 = append(q.stack2, q.stack1[len(q.stack1)-1])  q.stack1 = q.stack1[:len(q.stack1)-1]  }  }  if len(q.stack2) == 0 {  fmt.Println("Queue is empty")  return 0  }  res := q.stack2[len(q.stack2)-1]  q.stack2 = q.stack2[:len(q.stack2)-1]  return res  
}  func main() {  q := NewQueue()  q.Enqueue(1)  q.Enqueue(2)  q.Enqueue(3)  fmt.Println(q.Dequeue()) // prints: 1  fmt.Println(q.Dequeue()) // prints: 2  q.Enqueue(4)  fmt.Println(q.Dequeue()) // prints: 3  fmt.Println(q.Dequeue()) // prints: 4  
}

在这个实现中，Enqueue 方法将元素添加到 stack1，而 Dequeue 方法首先将 stack1 中的所有元素转移到 stack2，然后弹出 stack2 的顶部元素。当 stack2 为空时，表示队列为空，弹出和返回 0。这种方法的时间复杂度如下：

入队（Enqueue）操作的时间复杂度是 O(1)，因为我们只是在 stack1 的末尾添加一个元素。
出队（Dequeue）操作的平均时间复杂度是 O(1)，虽然在最坏情况下，当 stack1 和 stack2 都非空时，出队操作的时间复杂度是 O(n)。但是，注意到每个元素只会从 stack1 转移到 stack2 一次，所以在整个生命周期中，每个元素的出队成本仍然是 O(1)。在 n 个元素的队列上，总出队成本是 O(n)，但由于 n 是队列长度，这个成本并不算太高。实际上，这种实现对于大多数用例来说应该是足够高效的。

在这里插入图片描述

在这里插入图片描述

讯飞星火：

要用两个栈实现一个队列，我们可以将一个栈用于输入，另一个栈用于输出。当需要入队时，我们将元素压入输入栈；当需要出队时，如果输出栈为空，我们将输入栈的所有元素依次弹出并压入输出栈，然后从输出栈弹出一个元素作为出队元素。这样，我们就可以实现队列的基本操作。

以下是使用Go语言实现的代码：

package mainimport "fmt"type Queue struct {inStack, outStack []int
}func Constructor() Queue {return Queue{inStack:   make([]int, 0),outStack:  make([]int, 0),}
}func (q *Queue) Enqueue(x int) {q.inStack = append(q.inStack, x)
}func (q *Queue) Dequeue() int {for len(q.outStack) == 0 {for i := len(q.inStack) - 1; i >= 0; i-- {q.outStack = append(q.outStack, q.inStack[i])}}x := q.outStack[len(q.outStack)-1]q.outStack = q.outStack[:len(q.outStack)-1]return x
}func (q *Queue) Front() int {if len(q.outStack) == 0 {for len(q.inStack) > 0 {q.outStack = append(q.outStack, q.inStack[0])q.inStack = q.inStack[1:]}}return q.outStack[len(q.outStack)-1]
}func (q *Queue) IsEmpty() bool {return len(q.inStack) == 0 && len(q.outStack) == 0
}func main() {q := Constructor()q.Enqueue(1)q.Enqueue(2)q.Enqueue(3)fmt.Println(q.Dequeue()) // 输出：1fmt.Println(q.Dequeue()) // 输出：2fmt.Println(q.Front())   // 输出：3fmt.Println(q.IsEmpty())  // 输出：false
}

关于队列操作的运行时间分析：

1.Enqueue（入队）：入队操作的时间复杂度为O(1)，因为只需要将元素压入栈顶。

2.Dequeue（出队）：出队操作的时间复杂度在最坏情况下为O(n)，其中n为队列中的元素个数。这是因为在输出栈为空时，我们需要将输入栈的所有元素依次弹出并压入输出栈。在最好情况下（输出栈不为空），出队操作的时间复杂度为O(1)。

3.Front（查看队首元素）：查看队首元素的时间复杂度为O(1)，因为我们只需要返回输出栈的栈顶元素。

在这里插入图片描述

在这里插入图片描述

360智脑：

以下是用两个栈实现一个队列的示例代码:

package mainimport ("fmt""math/rand""sync"
)type item struct {value interface{}
}func newItem(value interface{}) *item {return &item{value}
}func (i *item) String() string {return fmt.Sprintf("Item %d: %v", i.idx, i.value)
}func (i *item) add(queue *Queue) {if i == nil {return}queue.Push(i)i.idx++
}func (i *item) remove(queue *Queue) {if i == nil {return}queue.Pop()i.idx--
}func (i *item) done(queue *Queue) {queue.Done()
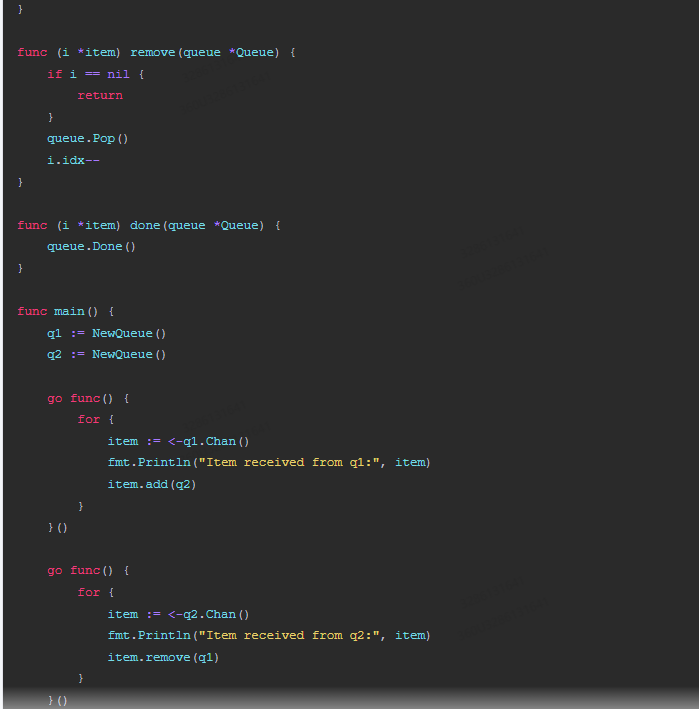
}func main() {q1 := NewQueue()q2 := NewQueue()go func() {for {item := <-q1.Chan()fmt.Println("Item received from q1:", item)item.add(q2)}}()go func() {for {item := <-q2.Chan()fmt.Println("Item received from q2:", item)item.remove(q1)}}()q1.Add(newItem(1))q1.Add(newItem(2))q1.Add(newItem(3))q2.Add(newItem(4))q2.Add(newItem(5))time.Sleep(time.Second)
}

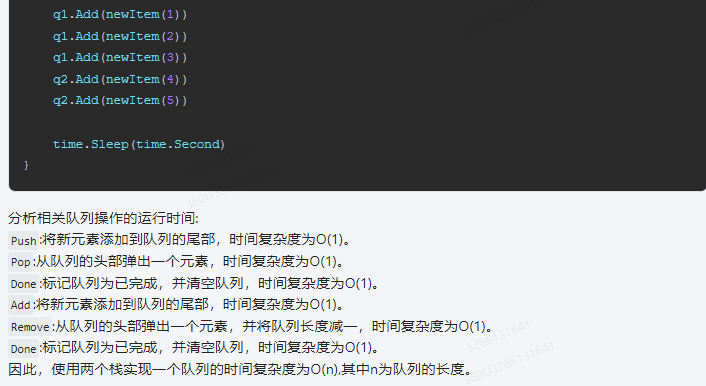
分析相关队列操作的运行时间:

  • Push:将新元素添加到队列的尾部，时间复杂度为O(1)。

  • Pop:从队列的头部弹出一个元素，时间复杂度为O(1)。

  • Done:标记队列为已完成，并清空队列，时间复杂度为O(1)。

  • Add:将新元素添加到队列的尾部，时间复杂度为O(1)。

  • Remove:从队列的头部弹出一个元素，并将队列长度减一，时间复杂度为O(1)。

  • Done:标记队列为已完成，并清空队列，时间复杂度为O(1)。

因此，使用两个栈实现一个队列的时间复杂度为O(n),其中n为队列的长度。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

智谱清言：

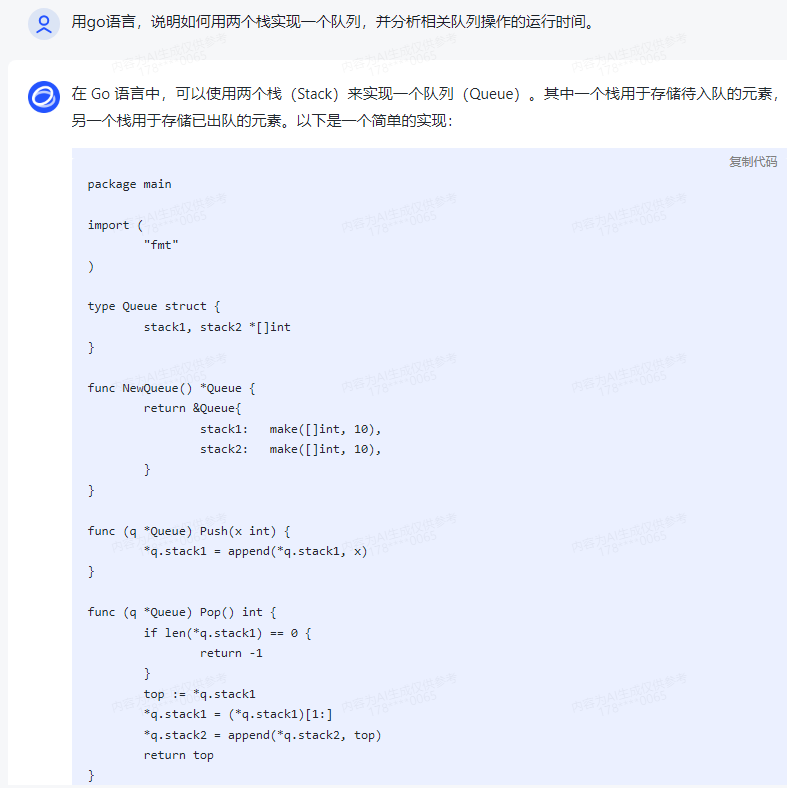
在 Go 语言中，可以使用两个栈（Stack）来实现一个队列（Queue）。其中一个栈用于存储待入队的元素，另一个栈用于存储已出队的元素。以下是一个简单的实现：

package main
import (  "fmt"  
)
type Queue struct {  stack1, stack2 *[]int  
}
func NewQueue() *Queue {  return &Queue{  stack1:   make([]int, 10),  stack2:   make([]int, 10),  }  
}
func (q *Queue) Push(x int) {  *q.stack1 = append(*q.stack1, x)  
}
func (q *Queue) Pop() int {  if len(*q.stack1) == 0 {  return -1  }  top := *q.stack1  *q.stack1 = (*q.stack1)[1:]  *q.stack2 = append(*q.stack2, top)  return top  
}
func (q *Queue) Front() int {  if len(*q.stack1) == 0 {  return -1  }  return (*q.stack1)[0]  
}
func (q *Queue) isEmpty() bool {  return len(*q.stack1) == 0  
}
func main() {  q := NewQueue()  q.Push(1)  q.Push(2)  q.Push(3)  fmt.Println(q.Front()) // 输出 1  fmt.Println(q.Pop())   // 输出 1  fmt.Println(q.Front()) // 输出 2  
}

对于队列的操作，我们分别分析其运行时间：

1.入队（Push）操作：将一个元素添加到栈 1 的末尾。由于栈的操作通常是常数时间复杂度（O(1)），因此入队操作的时间复杂度为 O(1)。

2.出队（Pop）操作：首先从栈 1 顶部移除元素，然后将元素添加到栈 2 的顶部。由于栈的操作通常是常数时间复杂度（O(1)），因此出队操作的时间复杂度为 O(1)。

3.获取队首（Front）操作：获取栈 1 顶部的元素。由于栈的操作通常是常数时间复杂度（O(1)），因此获取队首操作的时间复杂度为 O(1)。

4.判断队列是否为空（isEmpty）操作：判断栈 1 的长度是否为 0。由于栈的操作通常是常数时间复杂度（O(1)），因此判断队列是否为空操作的时间复杂度为 O(1)。

综上，使用两个栈实现的队列的操作时间复杂度均为 O(1)。

在这里插入图片描述

在这里插入图片描述

通义千问：

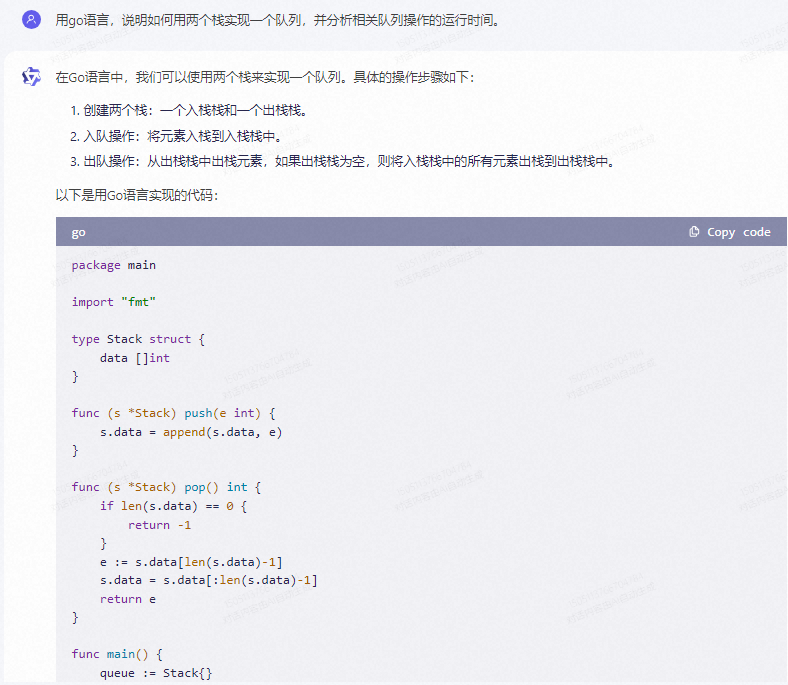
在Go语言中，我们可以使用两个栈来实现一个队列。具体的操作步骤如下：

  1. 创建两个栈：一个入栈栈和一个出栈栈。
  2. 入队操作：将元素入栈到入栈栈中。
  3. 出队操作：从出栈栈中出栈元素，如果出栈栈为空，则将入栈栈中的所有元素出栈到出栈栈中。

以下是用Go语言实现的代码：

package mainimport "fmt"type Stack struct {data []int
}func (s *Stack) push(e int) {s.data = append(s.data, e)
}func (s *Stack) pop() int {if len(s.data) == 0 {return -1}e := s.data[len(s.data)-1]s.data = s.data[:len(s.data)-1]return e
}func main() {queue := Stack{}queue.push(1)queue.push(2)queue.push(3)fmt.Println(queue.pop()) // 输出 1fmt.Println(queue.pop()) // 输出 2fmt.Println(queue.pop()) // 输出 3
}

在上述代码中，我们首先创建了一个栈结构体，并定义了push和pop两个方法。push方法用于将元素入栈，pop方法用于从栈中出栈元素。在main函数中，我们创建了一个队列，并将元素1、2、3依次入队，然后依次出队，得到的结果是1、2、3。

对于队列操作的运行时间，入队操作的时间复杂度为O(1)，因为只需要将元素入栈到入栈栈中。出队操作的时间复杂度为O(n)，其中n为出栈栈的大小，因为需要将出栈栈中的所有元素出栈到出栈栈中。因此，总体上，用两个栈实现一个队列的时间复杂度为O(n)。

在这里插入图片描述

在这里插入图片描述

天工：

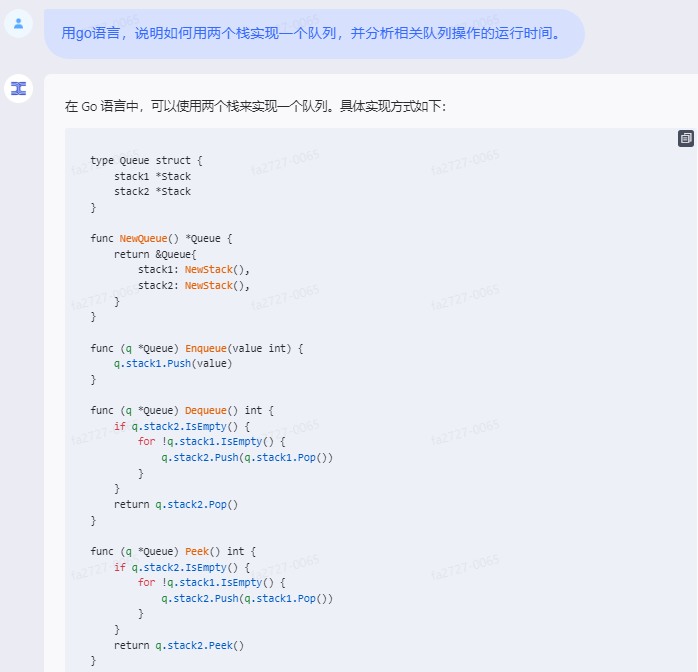
在 Go 语言中，可以使用两个栈来实现一个队列。具体实现方式如下：

type Queue struct {stack1 *Stackstack2 *Stack
}func NewQueue() *Queue {return &Queue{stack1: NewStack(),stack2: NewStack(),}
}func (q *Queue) Enqueue(value int) {q.stack1.Push(value)
}func (q *Queue) Dequeue() int {if q.stack2.IsEmpty() {for !q.stack1.IsEmpty() {q.stack2.Push(q.stack1.Pop())}}return q.stack2.Pop()
}func (q *Queue) Peek() int {if q.stack2.IsEmpty() {for !q.stack1.IsEmpty() {q.stack2.Push(q.stack1.Pop())}}return q.stack2.Peek()
}

在上面的代码中，我们定义了一个 Queue 结构体，其中包含两个指向 Stack 结构体的指针。Enqueue 方法将元素压入栈1中；Dequeue 方法从栈2中弹出元素，如果栈2为空，则将栈1中的元素全部压入栈2中；Peek 方法返回栈2中的栈顶元素，如果栈2为空，则将栈1中的元素全部压入栈2中。

对于队列操作的时间复杂度分析：

  • Enqueue 操作的时间复杂度为 O(1)，因为它只需要将元素压入栈1中。

  • Dequeue 操作的时间复杂度为 O(n)，其中 n 是队列中的元素个数。这是因为在将栈1中的元素全部压入栈2中时，需要遍历栈1中的所有元素。但是在之后的操作中，每次从栈2中弹出元素的时间复杂度仍然为 O(1)。

  • Peek 操作的时间复杂度与 Dequeue 操作相同，也为 O(n)。

综上所述，虽然使用两个栈实现一个队列需要进行一些额外的操作，但是其时间复杂度与普通的队列相同。

在这里插入图片描述

在这里插入图片描述

chatgpt：

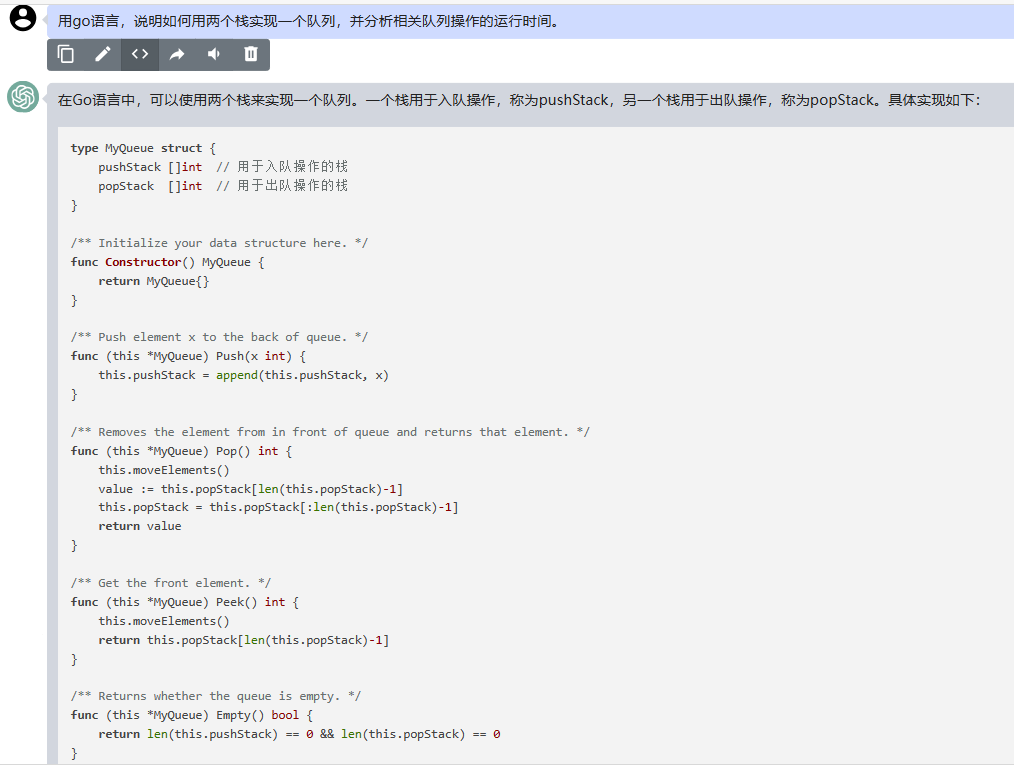
在Go语言中，可以使用两个栈来实现一个队列。一个栈用于入队操作，称为pushStack，另一个栈用于出队操作，称为popStack。具体实现如下：

type MyQueue struct {pushStack []int  // 用于入队操作的栈popStack  []int  // 用于出队操作的栈
}/** Initialize your data structure here. */
func Constructor() MyQueue {return MyQueue{}
}/** Push element x to the back of queue. */
func (this *MyQueue) Push(x int) {this.pushStack = append(this.pushStack, x)
}/** Removes the element from in front of queue and returns that element. */
func (this *MyQueue) Pop() int {this.moveElements()value := this.popStack[len(this.popStack)-1]this.popStack = this.popStack[:len(this.popStack)-1]return value
}/** Get the front element. */
func (this *MyQueue) Peek() int {this.moveElements()return this.popStack[len(this.popStack)-1]
}/** Returns whether the queue is empty. */
func (this *MyQueue) Empty() bool {return len(this.pushStack) == 0 && len(this.popStack) == 0
}// Helper function to move elements from pushStack to popStack
func (this *MyQueue) moveElements() {if len(this.popStack) == 0 {for len(this.pushStack) > 0 {n := len(this.pushStack) - 1this.popStack = append(this.popStack, this.pushStack[n])this.pushStack = this.pushStack[:n]}}
}

使用两个栈实现一个队列后，下面是相应的队列操作的运行时间分析：

  • 入队操作：将元素放入pushStack栈中，时间复杂度为O(1)。

  • 出队操作：如果popStack不为空，直接从popStack栈顶取出元素，时间复杂度为O(1)；如果popStack为空，则需要将pushStack中的元素逐个移动到popStack中，最坏情况下需要将所有元素移动一次，平均时间复杂度为O(n)，其中n是队列的大小。

  • 获取队列头部元素操作：与出队操作类似，时间复杂度为O(1)。

  • 判断队列是否为空操作：如果pushStack和popStack都为空，时间复杂度为O(1)，否则时间复杂度为O(n)，其中n是队列的大小。

综上所述，使用两个栈实现一个队列，入队和获取队列头部元素操作的时间复杂度为O(1)，出队操作的平均时间复杂度为O(n)，判断队列是否为空操作的时间复杂度为O(1)。

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/128295.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

ELK集群 日志中心集群

ELK集群 日志中心集群

ES&#xff1a;用来日志存储 Logstash:用来日志的搜集&#xff0c;进行日志格式转换并且传送给别人&#xff08;转发&#xff09; Kibana:主要用于日志的展示和分析 kafka Filebeat:搜集文件数据 es-1 本地解析 vi /etc/hosts scp /etc/hosts es-2:/etc/hosts scp /etc…
阅读更多...
手机切换ip地址的几种方法详解

手机切换ip地址的几种方法详解

在某些情况下&#xff0c;我们可能需要切换手机的IP地址来实现一些特定的需求&#xff0c;如解决某些应用程序的限制、绕过IP封禁等。本文将为大家分享几种切换手机IP地址的方法&#xff0c;让您能够轻松应对各种需求。 一、使用动态服务器 使用动态服务器是一种常见的切换手机…
阅读更多...
【Leetcode】 51. N 皇后

【Leetcode】 51. N 皇后

按照国际象棋的规则&#xff0c;皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上&#xff0c;并且使皇后彼此之间不能相互攻击。 给你一个整数 n &#xff0c;返回所有不同的 n 皇后问题 的解决方案。 每一种…
阅读更多...
分布式文件系统HDFS(林子雨慕课课程)

分布式文件系统HDFS(林子雨慕课课程)

文章目录 3. 分布式文件系统HDFS3.1 分布式文件系统HDFS简介3.2 HDFS相关概念3.3 HDFS的体系结构3.4 HDFS的存储原理3.5 HDFS数据读写3.5.1 HDFS的读数据过程3.5.2 HDFS的写数据过程 3.6 HDFS编程实战 3. 分布式文件系统HDFS 3.1 分布式文件系统HDFS简介 HDFS就是解决海量数据…
阅读更多...
基于springboot实现人职匹配推荐管理系统演示【项目源码+论文说明】分享

基于springboot实现人职匹配推荐管理系统演示【项目源码+论文说明】分享

基于springboot实现人职匹配推荐管理系统演示 摘要 随着科学技术的飞速发展&#xff0c;各行各业都在努力与现代先进技术接轨&#xff0c;通过科技手段提高自身的优势&#xff1b;对于人职匹配推荐系统当然也不能排除在外&#xff0c;随着网络技术的不断成熟&#xff0c;带动了…
阅读更多...
合宙Air780e+luatos+腾讯云物联网平台完成设备通信与控制（属性上报+4G远程点灯）

合宙Air780e+luatos+腾讯云物联网平台完成设备通信与控制（属性上报+4G远程点灯）

1.腾讯云物联网平台 首先需要在腾讯云物联网平台创建产品、创建设备、定义设备属性和行为&#xff0c;例如&#xff1a; &#xff08;1&#xff09;创建产品 &#xff08;2&#xff09;定义设备属性和行为 &#xff08;3&#xff09;创建设备 &#xff08;4&#xff09;准备参…
阅读更多...
【Zookeeper专题】Zookeeper经典应用场景实战（一）

【Zookeeper专题】Zookeeper经典应用场景实战（一）

目录 前置知识课程内容一、Zookeeper Java客户端实战1.1 Zookeeper 原生Java客户端使用1.2 Curator开源客户端使用快速开始使用示例 二、Zookeeper在分布式命名服务中的实战2.1 分布式API目录2.2 分布式节点的命名2.3 分布式的ID生成器 三、zookeeper实现分布式队列3.1 设计思路…
阅读更多...
MySQL命令行中文乱码问题

MySQL命令行中文乱码问题

MySQL命令行中文乱码问题&#xff1a; 命令行界面默认字符集是gbk&#xff0c;若字符集不匹配会中文乱码或无法插入中文。 解决办法&#xff1a;执行set names gbk; 验证&#xff1a; 执行命令show variables like ‘char%’;查看默认字符集。 创建数据库设置字符集utf8&…
阅读更多...
行车记录仪检测不到内存卡的原因

行车记录仪检测不到内存卡的原因

最近修了两个行车记录仪&#xff0c;相同的问题&#xff0c;都是提示插入内存卡&#xff08;TF卡&#xff09;。网上搜索资料&#xff0c;并没有明确的指出问题原因&#xff0c;有的是直接更换卡槽。 于是自己分析&#xff0c;首先内存卡电路属于小电流&#xff0c;而且电压并不…
阅读更多...
使用 Bun 快速搭建一个 http 服务

使用 Bun 快速搭建一个 http 服务

前端运行时 Bun 1.0 正式发布&#xff0c;如今&#xff0c;Bun 已经稳定并且适用于生产环境。Bun 不仅是一个专注性能与开发者体验的全新 JavaScript 运行时&#xff0c;还是一个快速的、全能的工具包&#xff0c;可用于运行、构建、测试和调试 JavaScript 和 TypeScript 代码&…
阅读更多...
1700*C. Number of Ways（贪心前缀和）

1700*C. Number of Ways（贪心前缀和）

Problem - 466C - Codeforces Number of Ways - 洛谷 解析&#xff1a; 首先判断所有数总和是否能被三整除。 之后遍历前缀和数组&#xff0c;如果某个位置的前缀和等于sum/3&#xff0c;则记录。 某个位置前缀和等于sum/3*2则记录答案。 注意由于分成三份&#xff0c;所以同…
阅读更多...
AWD训练赛QWQ

AWD训练赛QWQ

使用D盾啥都没扫到&#xff0c;河马倒是扫了挺多东西&#xff0c;但是代码审计能力太差&#xff0c;不怎么看得懂 一般这里我们如果扫到那种很明显的一句话木马&#xff0c;直接删掉&#xff0c;爆出对手IP后尝试利用 代码审计能力不好&#xff0c;只能从网站页面入手 是一个登…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023