论文题目:FRESHLLMS:REFRESHING LARGE LANGUAGE MODELS WITH SEARCH ENGINE AUGMENTATION
论文地址:https://arxiv.org/pdf/2310.03214.pdf
论文由Google、University of Massachusetts Amherst、OpenAI联合发布。
大部分大语言模型只会训练一次,不会被频繁的更新,训练用到的知识会慢慢过时,所以它无法适应变化的世界。论文作者提出了动态问答的基准测试,称为FRESHQA,并且提出了一种简单的解决问题的方法,FRESHPROMPT。
FRESHQA收集的问题根据难度可以分别单跳和多跳两种,两种问题的区别在于是否需要多级的推理。而根据答案的性质问题可以分为1.永远不变;2.缓慢变化;3.快速变化;4.虚假前提。

测试集的评估模式也分别两种:1.RELAXED,它仅衡量主要答案是否正确; 2.STRICT,它衡量响应中的所有声明是否是事实和最新的(即没有幻觉)。
FRESHPROMPT 是一种简单而有效的方法,对于给定的问题,它通过提取所有最新和相关的信息(包括来自搜索用户也询问的相关问题的知识)来利用搜索引擎,并使用少样本上下文学习教模型推理检索到的证据并找出正确的答案。
搜索引擎返回内容如下图,serper api返回内容类似。

FRESHPROMPT的具体做法如下:
使用搜索引擎得到相关实时信息,并处理成统一的结构化信息:
1.对问题q进行逐字记录检索搜索引擎,并保留所有检索信息。
(搜索引擎使用google的serper api;搜索返回字段如下:relatedSearches,organic,searchParameters,knowledgeGraph,answerBox,peopleAlsoAsk,根据问题不同返回字段不同。)
2.将所有信息进行提取,生成内容为结构化的统一格式,证据E = {(s,d,t,x,h)的列表。
(符号表示如下:s:source, d:date, t:title, x:snippet, h:highlight)
3.对E的列表按时间进行排序。
为了帮助模型“理解”任务和期望输出,我们在输入提示的开头提供了输入输出示例的少量演示。每个演示都显示了模型示例问题和问题检索到的证据列表,然后对证据进行思维链推理,以找出最相关和最新的答案。最终的提问构造如下图。其中demonstrations表示输入输出示例的演示。

实验结果
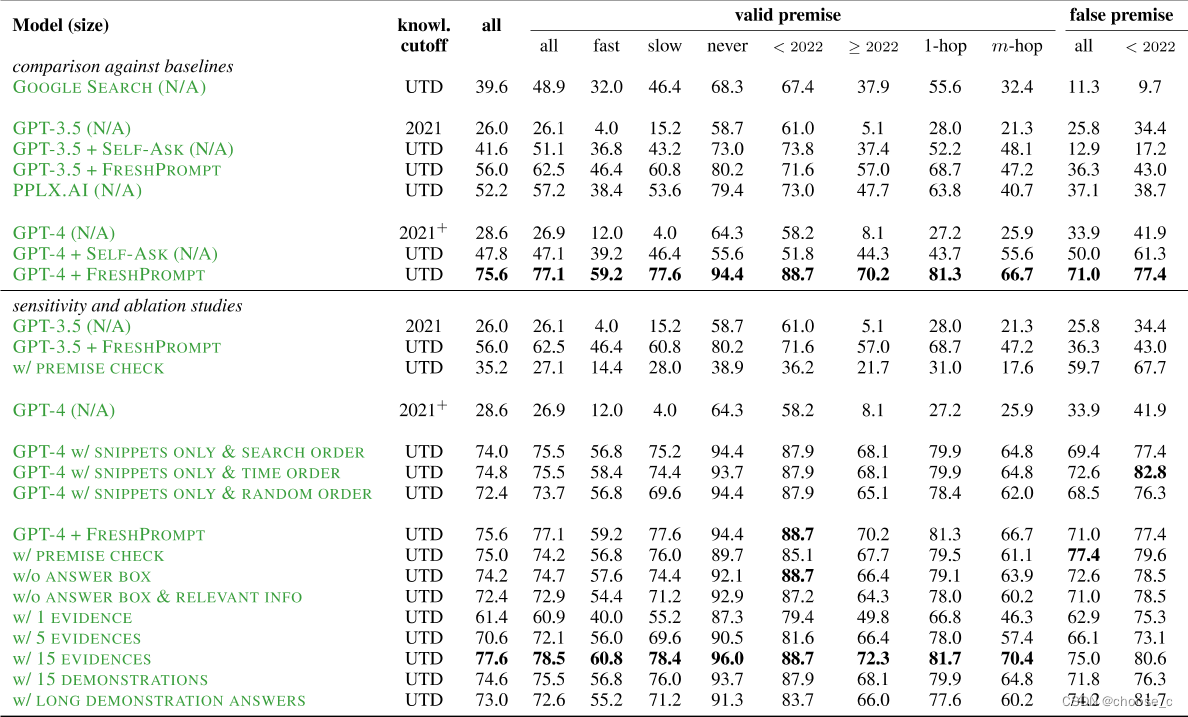
表中主要展示不同的模型和实验配置(消融实验)在FRESHQA数据集上的表现(STRICT)。
大模型选取了gpt3.5和gpt4。
google search表示直接使用google进行回复,选取结果为answer box(如有) 或者 第一个结果的 text snippet。
PPL.AI是一个将LLM和搜索引擎相结合以生成对用户查询的有用响应的答案引擎。
self-ask是一种使用情景学习的方法,教LLM将每个问题分解成更简单的子问题,然后通过谷歌搜索来回答。
对于FRESHPROMPT的设置,搜索答案的选取不同(snippets only、answer box relevant info)、搜索结果的排序不同(search order、time order、random order)、搜索结果数量不同(1、5、15,默认为10)、输入输出示例描述demonstrations数量不同、是否添加premise check(让模型进行错误前提检查)。
结论
1.FRESHPROMPT可以带来巨大的效果提升,因为外部实时数据的加入,使模型可以回答动态问题。
2.FRESHPROMPT比其他的搜索增强的方法效果好,对比方法为PPL.AI和+self-ask方法。3.premise check方法对与错误前提问题有效,但是同时也会降低有效前提问题的回答准确性。总体结果为弊大于利。
4.更全面更新的相关证据的效果会更好。time order>search order>>random order;搜索内容更加全面(不仅仅是text snippets)也会有利回复。
5.增加检索到的证据的数量进一步提高了 FRESHPROMPT效果,但要考虑大模型的token length limit。
6.冗长的演示(demonstrations)改进了复杂的问题,但也增加了幻觉。