归并排序递归方法和非递归方法详解-编程知识

文章目录

归并排序递归方法和非递归方法详解
- 1、归并排序（递归）
- - 1.1、归并排序思想（递归）
  - 1.2、排序过程（递归）图解
  - 1.3、归并排序（递归）代码
- 2、归并排序（非递归）
- - 2.1、归并排序（非递归）思想
  - 2.2、排序过程（非递归）图解
  - 2.3、归并排序（非递归）代码

归并排序递归方法和非递归方法详解

1、归并排序（递归）

1.1、归并排序思想（递归）

归并排序（递归）是采用分治的思想，对整个数组序列进行排序，即先把序列分成两段，再将这两段分成四段，再将这四段分成八段，直到每段序列长度小于等于1则返回（即先把长度1的序列排序，先让它有序）。先处理左边的序列，再处理右边的序列（这里以升序为例）。将长度为1的序列进行归并（这里使用了一个临时数组tmp保存当前归并后的有序序列），归并（归并过程看下边解释）结束后就有了一个序列长度为2的有序序列，然后把这长度为2的有序序列拷贝回原来的数组，以便于后续归并，然后把右边长度为1的序列归并为长度为2的有序序列，然后就把两个长度为2的有序序列（不一定两个序列长度一样，但是一定都是有序的）归并为长度为4的有序序列。以此类推，直到得到整个数组长度的有序序列。
归并过程：假设当前有两个长度分别为size1和size2的序列，对于此时的两个序列来说，已经分别都有序了（其中当序列长度为1的时候，即元素个数为1，每个序列肯定有序），那么直接对两个序列从前往后遍历，找到两个序列中更小的元素放到临时数组tmp中，直到一个序列遍历完，然后再将未遍历完的序列里的元素依次放到tmp中，这样就合并完了两个有序序列，合并成了一个有序序列。

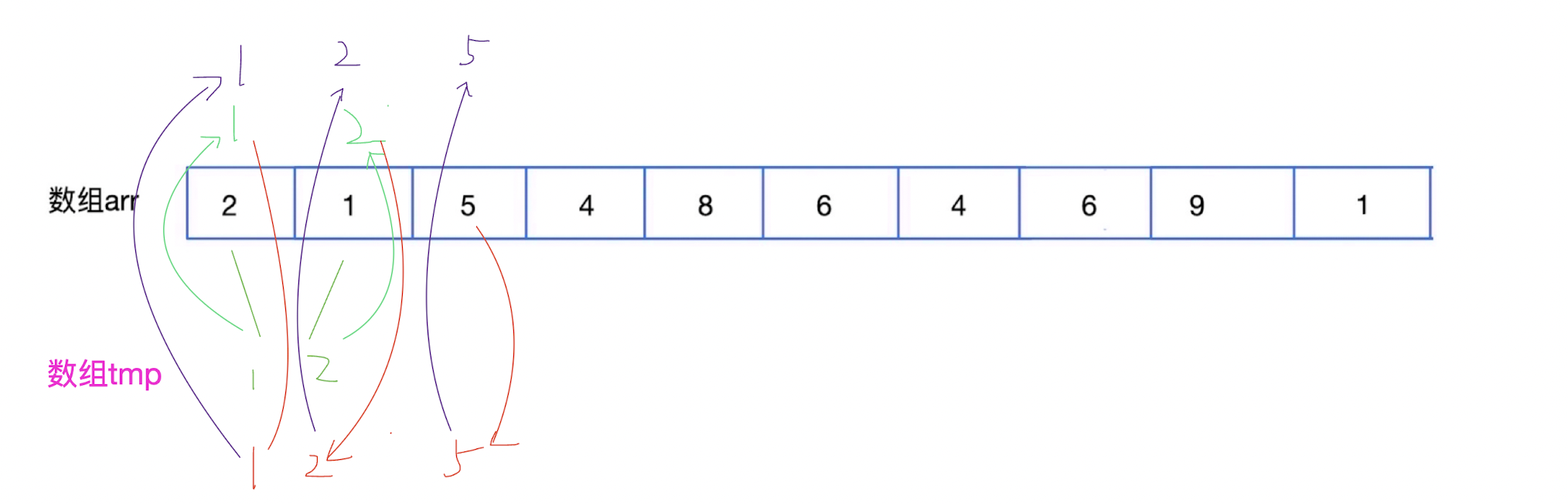
1.2、排序过程（递归）图解

先将序列分成两半，左边[left,mid]和右边[mid+1,right]其中mid = (left+right)/2。
再先对左边序列继续分成两半，直到分成序列长度小于等于1，则开始比较，将序列长度为1的两个序列合并为序列长度为2的有序序列，重复上面步骤，直到整个序列有序。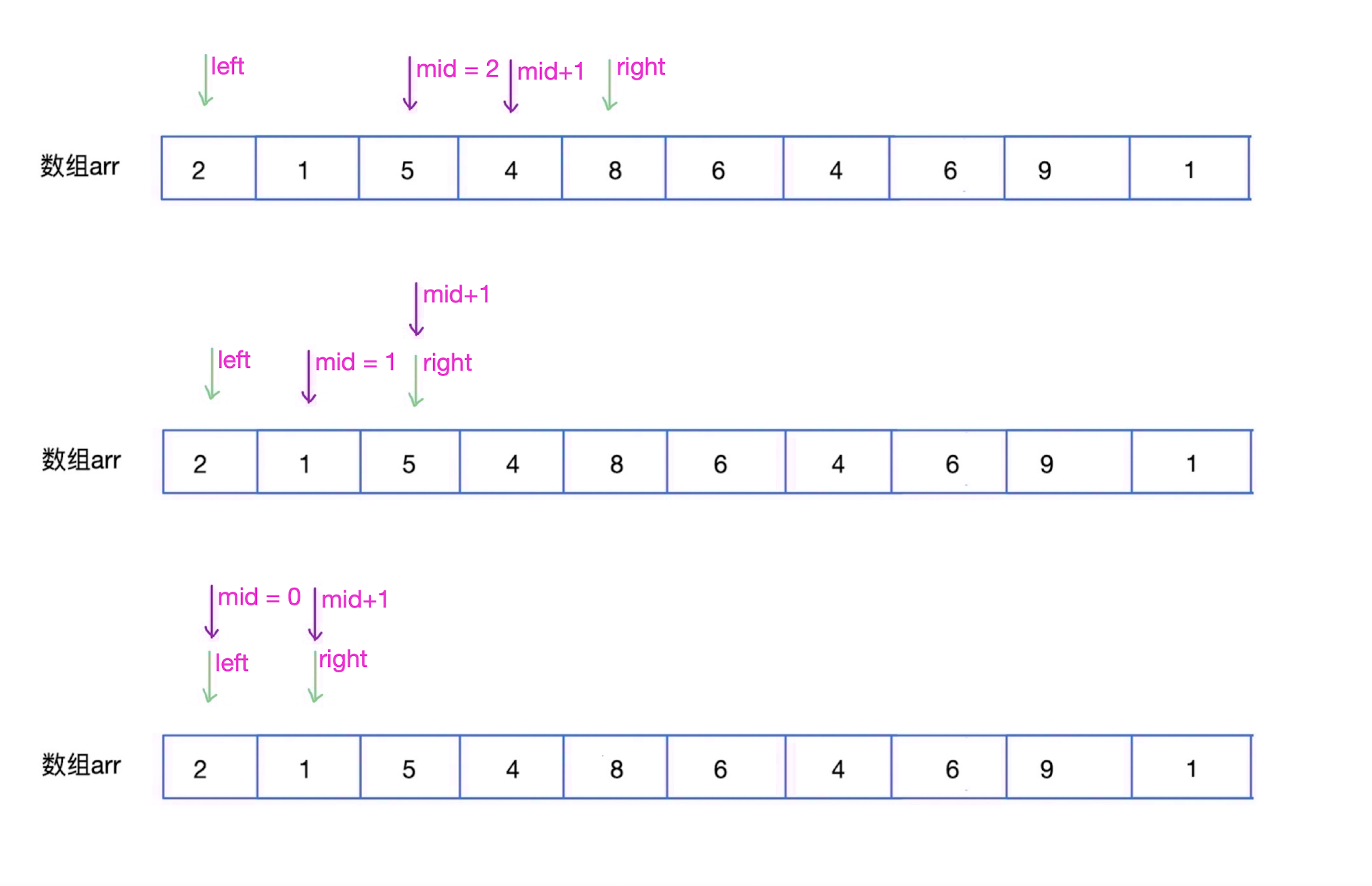
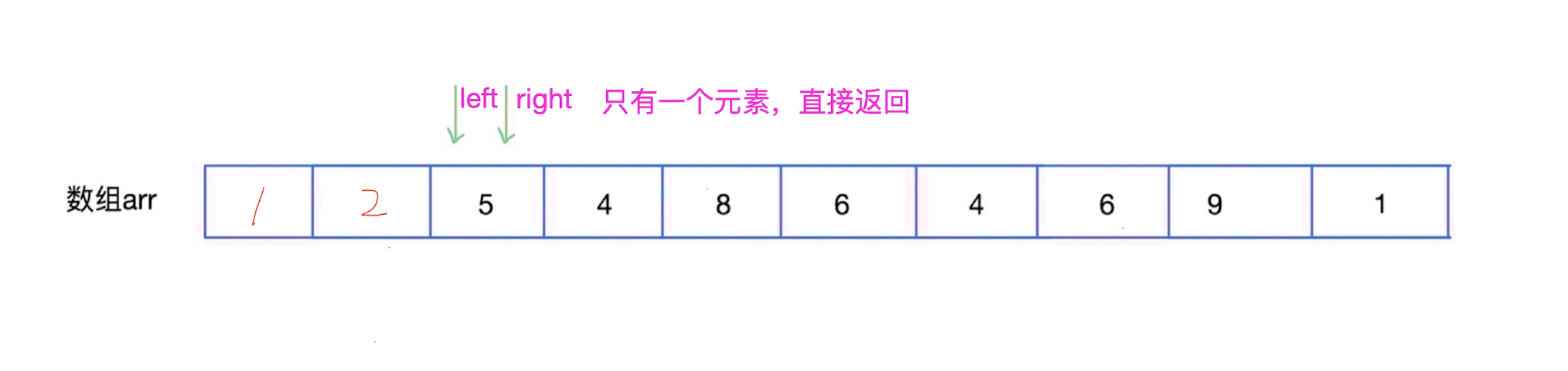
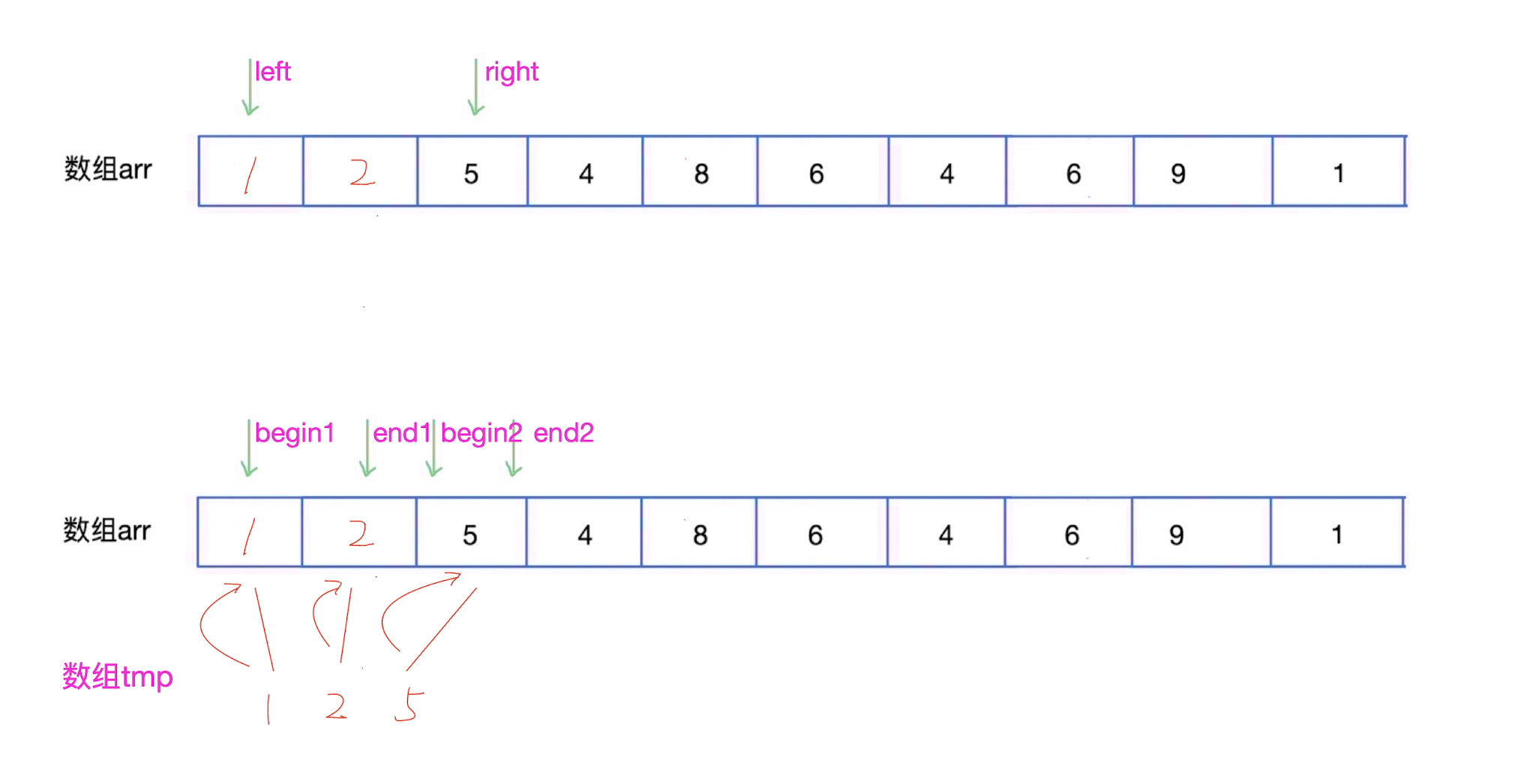
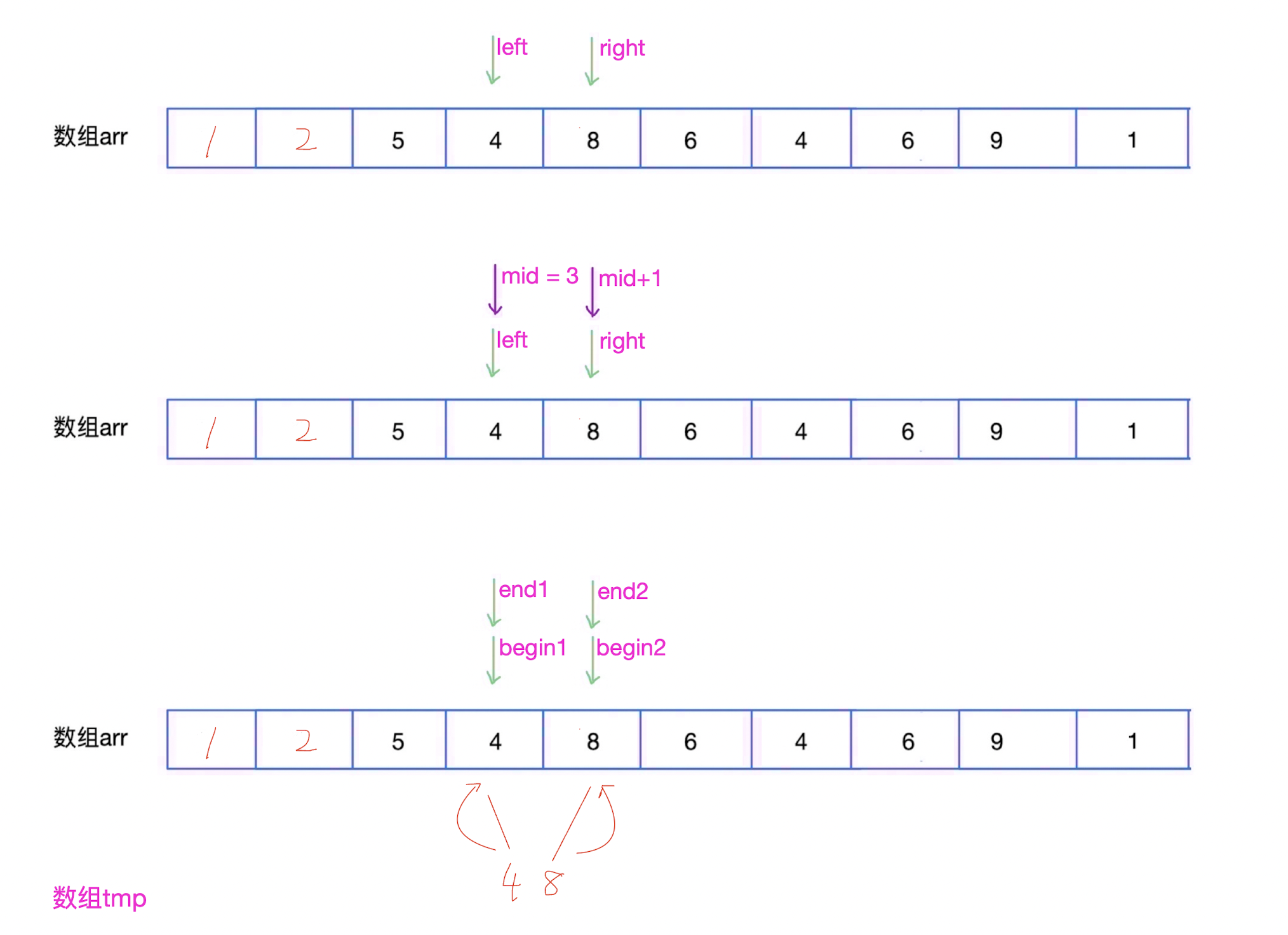
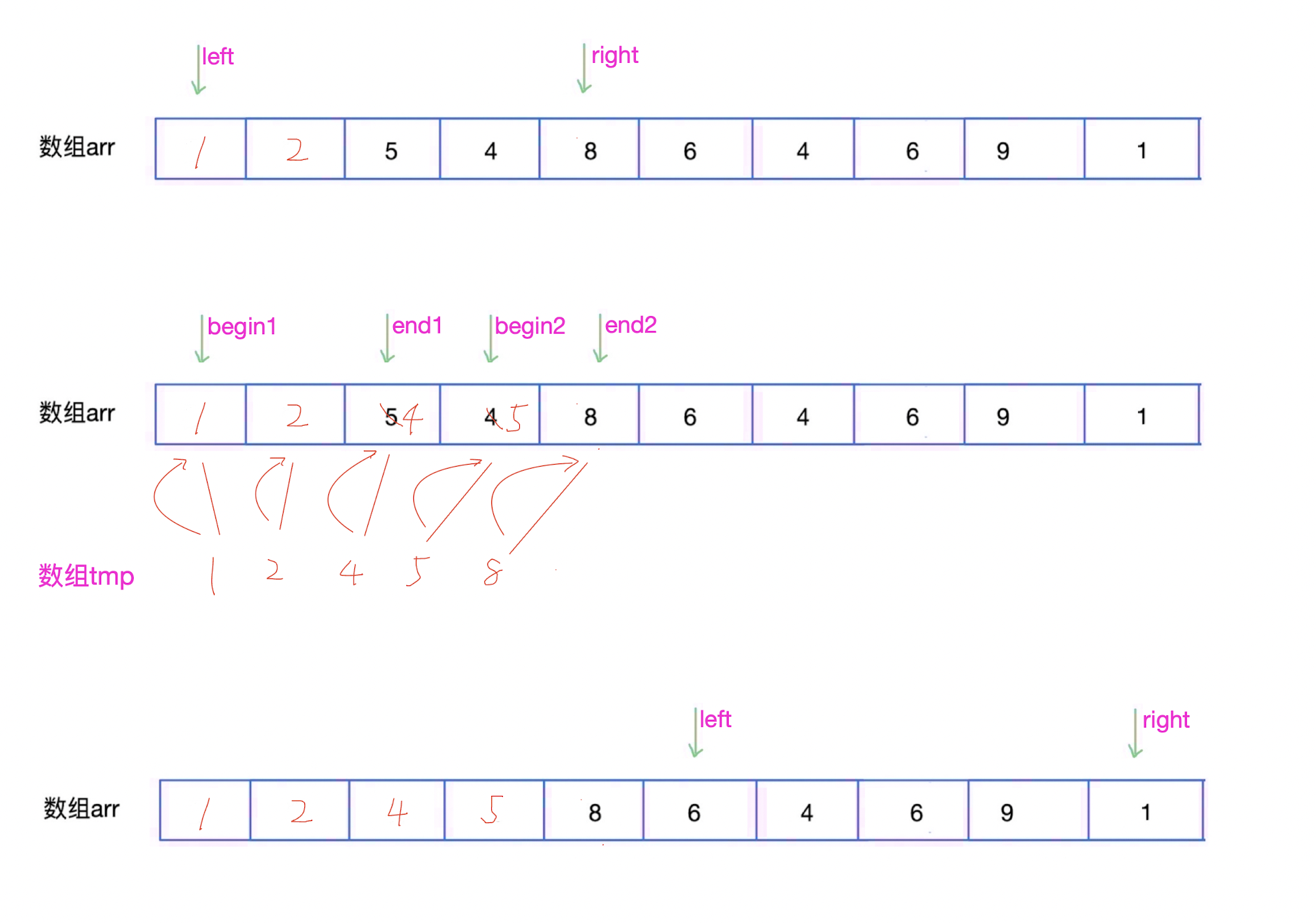
- 这里是部分图解，其他过程自行自考（和上述过程类似）。

1.3、归并排序（递归）代码

采用分治的思想，这里递归的过程类似二叉树的后续遍历（左子树–>右子树–>根）。

void _MergeSort(int *arr, int *tmp, int left, int right) {//剩一个元素或者left<rightif (left >= right)return;//二分法int mid = (left + right) / 2;_MergeSort(arr, tmp, left, mid);_MergeSort(arr, tmp, mid + 1, right);//归并到tmp数组，再拷贝回去int index = left;int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;while (begin1 <= end1 && begin2 <= end2) {if (arr[begin1] <= arr[begin2])tmp[index++] = arr[begin1++];elsetmp[index++] = arr[begin2++];}//还有没排完的while (end1 - begin1 >= 0) {tmp[index++] = arr[begin1++];}while (end2 - begin2 >= 0) {tmp[index++] = arr[begin2++];}//拷贝回去  -- 画图理解memcpy(arr + left, tmp + left, sizeof(int) * (right - left + 1));
}//归并排序 -- 递归方法
void MergeSort(int *arr, int begin, int end) {int n = end - begin + 1;int *tmp = (int *) malloc(sizeof(int) * n);if (tmp == NULL) {printf("malloc error");exit(-1);}_MergeSort(arr, tmp, 0, n - 1);free(tmp);
}

2、归并排序（非递归）

2.1、归并排序（非递归）思想

归并排序（非递归）是采用归并排序（递归）的逆向思维，即对于归并排序（递归）是将一个序列划分，一直划分到序列长度小于等于1才开始归并，将序列长度为1的两序列归并掉序列长度为2的有序序列，再将长度为2的的两个有序序列归并为长度为4的有序序列，直到整个序列有序。那么采用逆向思维的话，那我们可以先归并长度为1的两个有序序列，使其变成长度为2的有序序列，再归并两个长度为2的有序序列，使其变成长度为4的有序序列，重复这个过程。
- 注意：这里要注意序列的总长度不一定是2的指数倍，所以我们要注意下标越界问题：
  1. 这里我们每次归并都是采用两两归并，分为第一组数据（假设下标范围是[begin1,end1]）和第二组数据（假设下标范围是[begin2,end2]），如果第二组数据不存在了（begin2 >= n），则这次不用归并了。
  2. 如果第二组数据存在，但是长度小于第一组数据的长度（end2 >= n，为什么end2有可能大于等于n？因为两组数据的长度都是按2的指数倍来修改的），则修改这组数据的最右边元素的下标为n-1（最后一个元素下标）。

2.2、排序过程（非递归）图解

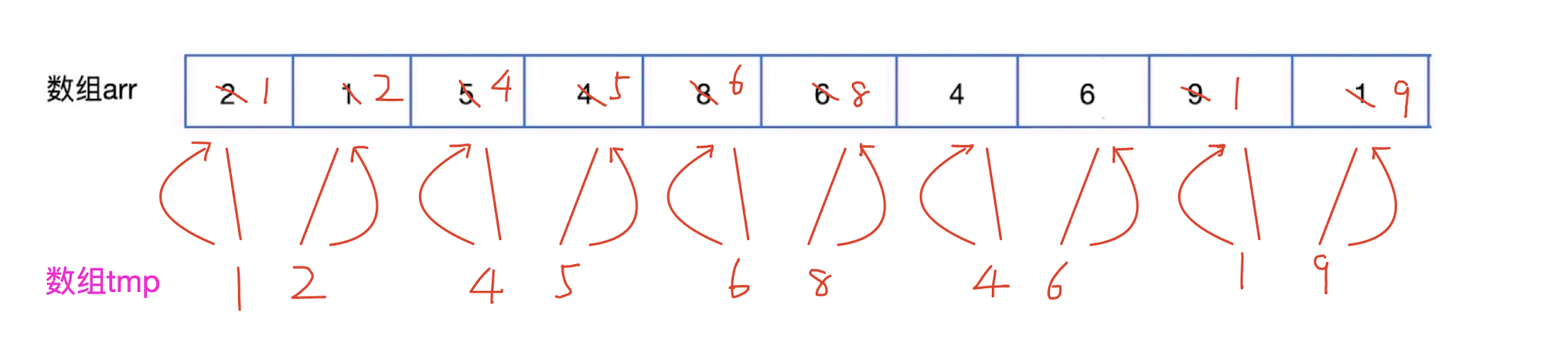
先把序列长度为1的序列归并为长度为2的有序序列。
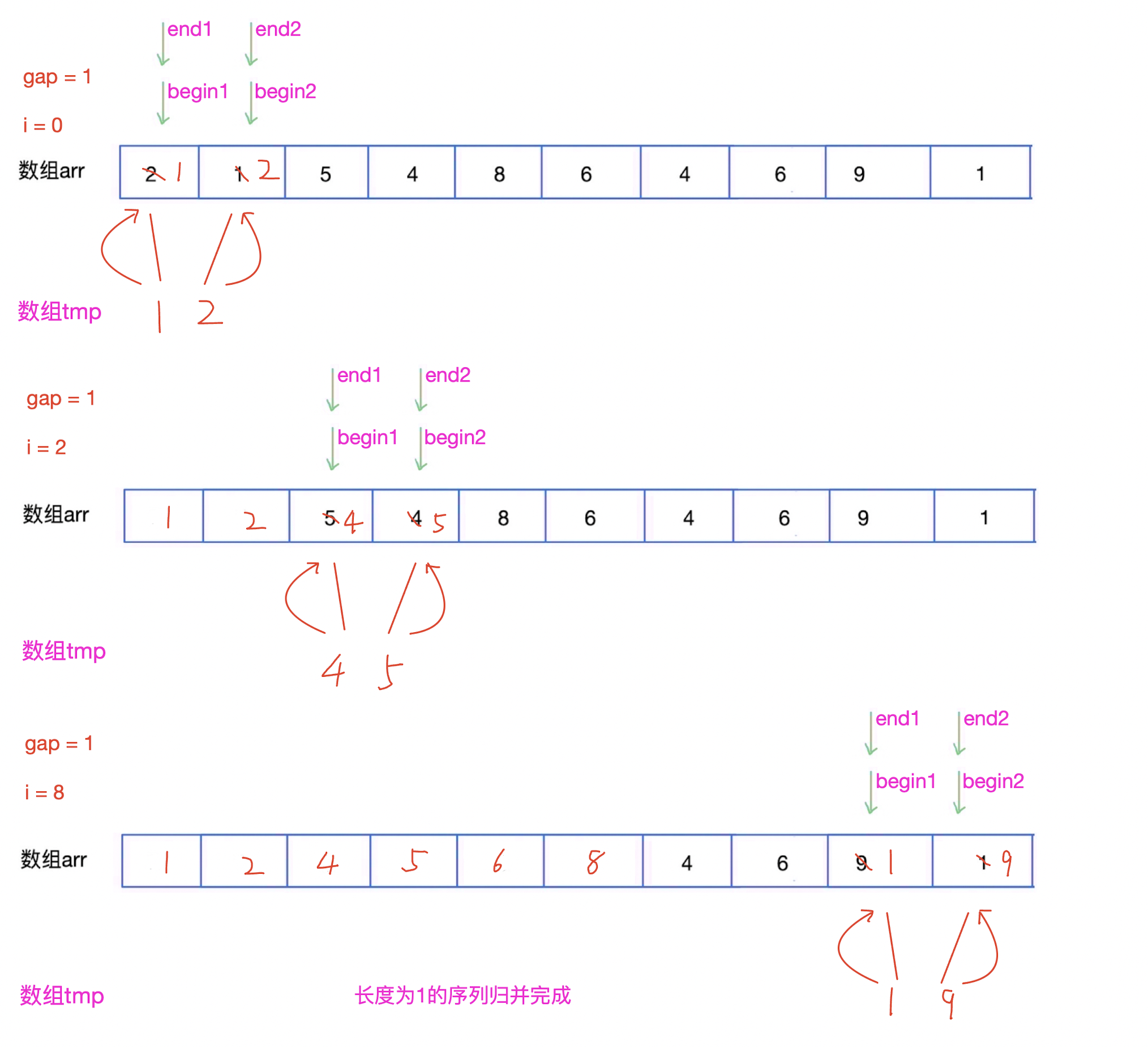
再把序列长度为2的序列归并为长度为4的有序序列。
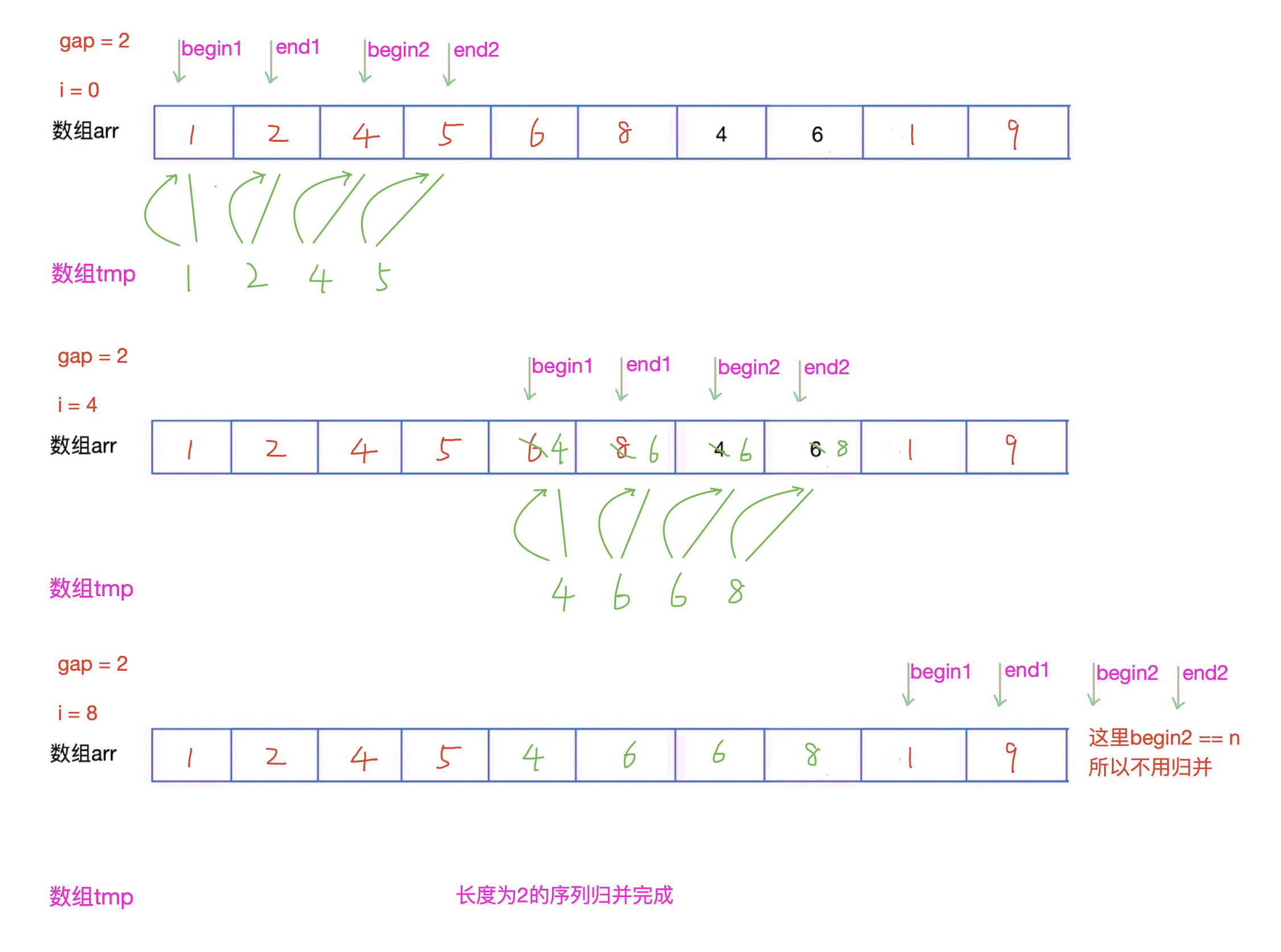
再把序列长度为4的序列归并为长度为8的有序序列。
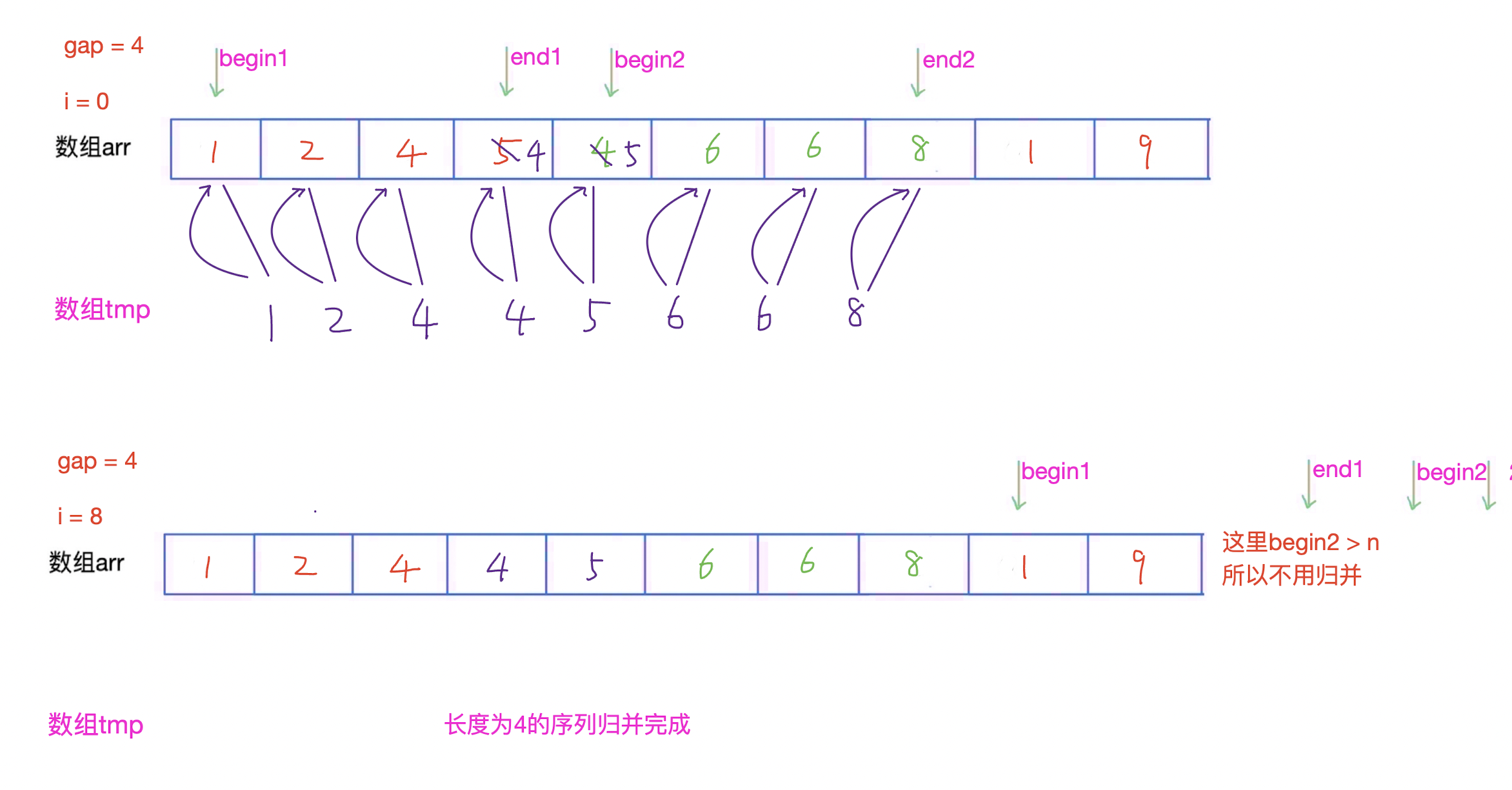
再把序列长度为8的序列归并为长度为10的有序序列。

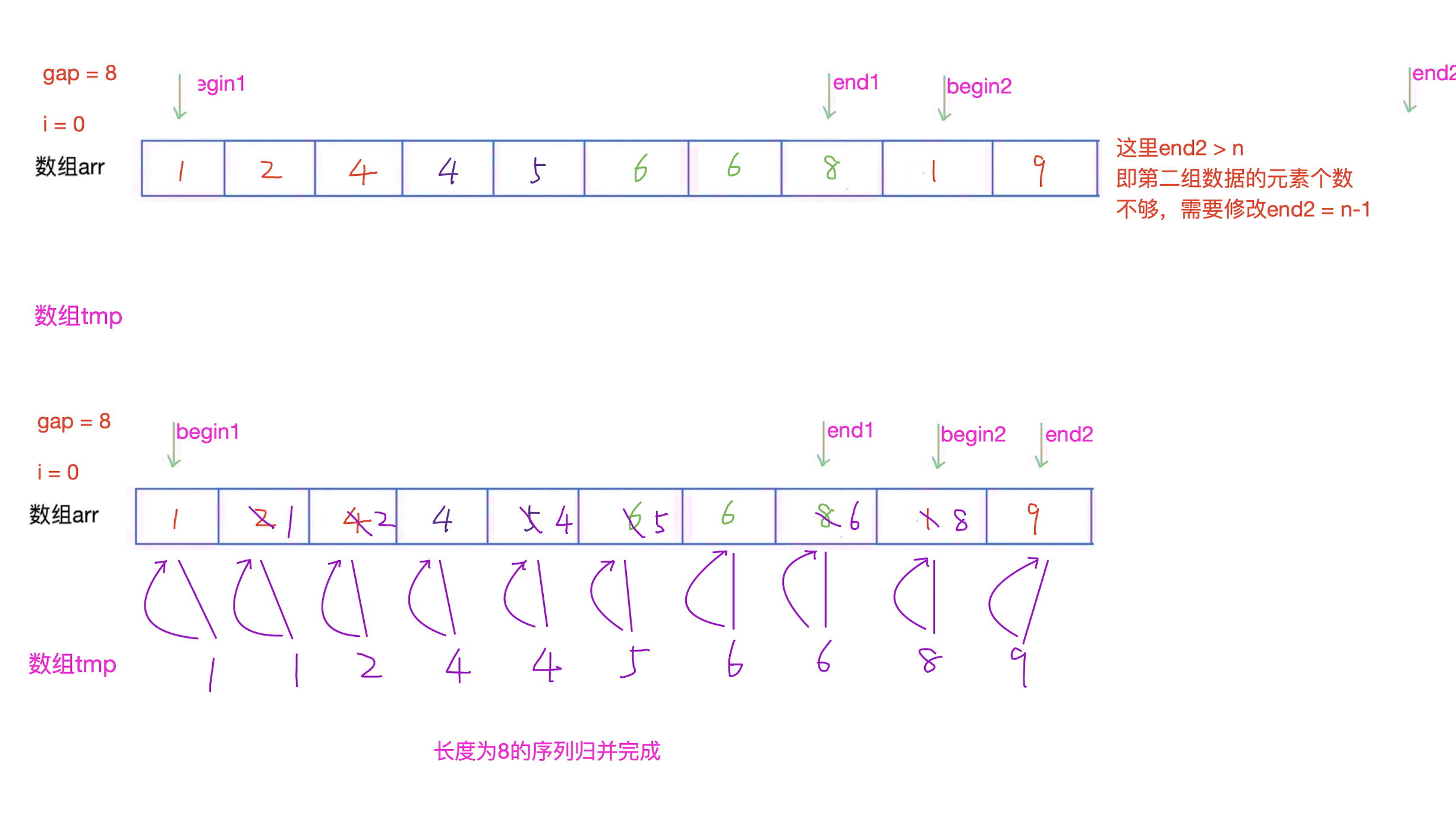
2.3、归并排序（非递归）代码

这里代码思想是容易想到的，难点是控制边界情况，防止下标越界：
- 因为序列的总长度不一定是2的指数倍，所以我们要注意下标越界问题：
  1. 这里我们每次归并都是采用两两归并，分为第一组数据（下标范围是[begin1,end1]）和第二组数据（下标范围是[begin2,end2]），如果第二组数据不存在了（begin2 >= n），则这次不用归并了。
  2. 如果第二组数据存在，但是长度小于第一组数据的长度（end2 >= n，为什么end2有可能大于等于n？因为两组数据的长度都是按2的指数倍来修改的），则修改这组数据的最右边元素的下标为n-1（最后一个元素下标）。
还有要注意的就是临时数组tmp拷贝回原数组的起始点和拷贝回去的元素个数：
- 起始点：tmp+i。因为i是每次归并的第一组元素的第一个元素的位置。
- 拷贝回去的元素个数：end2-i+1。因为end2指向的是每次归并的第二组元素的最后一个位置，i指向的是每次归并的第一组元素的第一个元素的位置。
每次归并的元素个数以2的指数倍增长。
for循环里的i在经过一次归并后，应该跳到下一次需要归并的第一组数据的第一个位置上。

//归并排序 -- 非递归方法
void MergeSortNonR(int *arr, int begin, int end) {int n = end - begin + 1;int *tmp = (int *) malloc(sizeof(int) * n);int gap = 1;while (gap < n) {for (int i = 0; i < n; i += 2 * gap) {int begin1 = i;int end1 = begin1 + gap - 1;int begin2 = end1 + 1;int end2 = begin2 + gap - 1;//这里得判断越界问题//第二组不存在，就不用归并了if (begin2 >= n) {//if(end1 >= n || begin2 >= n)也可以break;}if (end2 >= n) {end2 = n - 1;}int index = i;while (begin1 <= end1 && begin2 <= end2) {if (arr[begin1] <= arr[begin2])tmp[index++] = arr[begin1++];elsetmp[index++] = arr[begin2++];}//还有没排完的while (end1 - begin1 >= 0) {tmp[index++] = arr[begin1++];}while (end2 - begin2 >= 0) {tmp[index++] = arr[begin2++];}//拷贝回去  -- 画图理解
//            memcpy(arr + i, tmp + i, sizeof(int) * (2 * gap));memcpy(arr + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}
}