leetCode 15.三数之和双指针解法-编程知识

leetCode 15.三数之和双指针解法

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

>>思路和分析

举个例子：target = 0，nums = [-1,0,1,2,-1,-4]

nums.sort() nums = [-4,-1,-1,0,1,2]
0 - nums[i] = nums[left] + nums[right]
ans: [-1,-1,2] [-1,0,1]

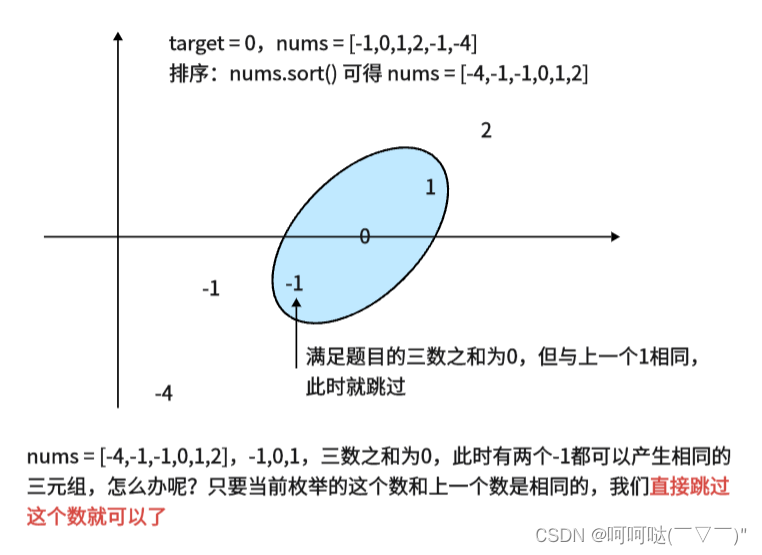
由于题目说三元组的顺序并不重要，比如[-1,0,1]和[-1,1,0],这是同一个三元组（元素相同），题目的要求就相当于 i < j < k，然后我们可以枚举nums[i]，这样就把问题转换成剩下的这两个数相加，它等于-nums[i],也就转换成了两数之和这道题。最后这题还有一个要求，答案中不可以包含重复的三元组

思考🤔那什么时候会出现重复的三元组呢？

我们讲示例一的nums排好序，可以得到 nums = [-4,-1,-1,0,1,2]，-1,0,1，三数之和为0，此时有两个-1都可以产生相同的三元组，怎么办呢？只要当前枚举的这个数和上一个数是相同的，我们直接跳过这个数就可以了。

C++代码：target = -nums[i]，j 就是 left , k 就是 right

class Solution {
public:// O(n^2)vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(), nums.end()); // nlognvector<vector<int>> res;int n = nums.size();// O(n^2)for(int i=0;i<n-2;++i) {if(i>0 && nums[i] == nums[i-1]) continue; // 跳过重复数字if(nums[i] + nums[i+1] + nums[i+2] > 0) break; // 优化一if(nums[i] + nums[n-2] + nums[n-1] < 0) continue; // 优化二int j=i+1,k=n-1;int target = -nums[i];while(j<k) {int s = nums[j] + nums[k];if(s>target) --k;else if(s<target) ++j;else{res.push_back({nums[i],nums[j],nums[k]});for(++j;j<k && nums[j] == nums[j-1];++j);// 跳过重复数字for(--k;k>j && nums[k] == nums[k+1];--k);// 跳过重复数字}}}return res;}
};

C++代码：改成s = nums[i] + nums[j] + nums[k]

class Solution {
public:// O(n^2)vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(), nums.end()); // nlognvector<vector<int>> res;int n = nums.size();// O(n^2)for(int i=0;i<n-2;++i) {if(i>0 && nums[i] == nums[i-1]) continue; // 跳过重复数字if(nums[i] + nums[i+1] + nums[i+2] > 0) break; // 优化一if(nums[i] + nums[n-2] + nums[n-1] < 0) continue; // 优化二int j=i+1,k=n-1;while(j<k) {int s = nums[i] + nums[j] + nums[k];if(s>0) --k;else if(s<0) ++j;else{res.push_back({nums[i],nums[j],nums[k]});// ++j;// while(j<k && nums[j] == nums[j-1]) ++j;// --k;// while(k>j && nums[k] == nums[k+1]) --k;for(++j;j<k && nums[j] == nums[j-1];++j);// 跳过重复数字for(--k;k>j && nums[k] == nums[k+1];--k);// 跳过重复数字}}}return res;}
};