1 信息与消息
1.1 信息
1.1.1 信息的定义
信息是信息论中最基本、最重要的概念
香农信息的定义:信息是事物运动状态或存在方式的不确定描述
1.1.2 (香农)信息的度量
- 样本空间:对于我们需要描述的事物中,事物可能存在不同的状态,即事物展现出来的多种状态。那么为了便于形容事物的不同状态,我们把事物各种可能出现的不同状态,即所有可能选择的消息的集合,称为样本空间
- 概率测度:对于离散消息的集合,概率测度为集合中的每一个符号的一个概率 (先验概率)
- 概率空间:将样本空间与其对应的概率测度称为一个概率空间
\[\begin{bmatrix}
X \\
P(x)
\end{bmatrix}
=
\begin{bmatrix}
a_{1}, a_{2},\dots, a_{q} \\
P(a_{1}), P(a_{2}), \dots, P(a_{q})
\end{bmatrix} \\
\]
\(P(a_{i})\) 为集合中出现符号为 \(a_{i}\) 的概率,即先验概率
- 自信息:在接收端中,我们对于尚未接收到的信息是不确定的,这种不确定性与对应符号的先验概率是成反比的,如果这个符号的先验概率大,即发出该符号的概率大,那么收到该符号的可能性就小,那么其不确定性就小。故我们定义对富豪的先验概率的倒数取对数,得到的内容为消息 (符号) 的自信息,即这样定义的不确定性称为该消息 (符号) 的自信息:
\[I(a_{i})=\log \frac{1}{P(a_{i})}
\]
- 互信息:由于信息传输的信道可能受到外界干扰,符号在传输过程中可能被改变,故收到某个符号的概率不一定与其先验概率一致。此时我们假设发送的信息为 \(a_{i}\),而收到的信息为 \(b_{j}\),我们称条件概率 \(P(a_{i}|b_{j})\) 为后验概率,其描述了当接收到的符号为 \(b_{j}\) 时,发送端发送的为 \(a_{i}\) 的概率。显然,对于后验概率,我们依然可以得到一个关于后验概率的不确定性,其描述的含义应当为接收方收到符号 \(b_{j}\) 时,其可能实际上为发送方发送的符号为 \(a_{i}\) 的不确定性。将先验概率所产生的不确定性减去后验概率所产生的不确定性,这就是收信者获得的信息量,即为互信息:
\[I(a_{i};b_{j})=\log \frac{1}{P(a_{i})}-\log \frac{1}{P(a_{i}|b_{j})}
\]
需要注意的是,互信息也是一种不确定性,自信息 \(\log \frac{1}{P(a_{i})}\) 衡量的是发送该符号的不确定性,而后验概率的自信息 \(\log \frac{1}{P(a_{i}|b_{j})}\) 则是发送 \(a_{i}\) 收到 \(b_{j}\) 的不确定性,将发送 \(a_{i}\) 的不确定性减去接收时发送 \(a_{i}\) 收到 \(b_{j}\) 的不确定性,则剩余的不确定性为实际收到 \(a_{i}\) 时的信息量,称为互信息
1.2 消息
1.2.1 消息的定义
用文字、符号、数据、语言、音符、图片、图像等能够被人们感觉器官所感知的形式,把客观物质运动和主观思维活动的状态表达出来就成为了消息
1.2.2 信号的定义
把消息转化为适合信道传输的物理量,这种物理量称为信号
2 关于信息论研究
2.1 信息论研究的对象
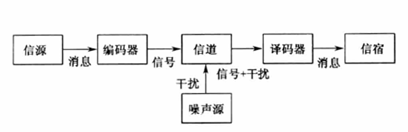
以下为通信系统模型,信息论所研究的对象就是这种统一的通信系统模型
- 信源:产生消息与消息序列的源
- 编码器:编码将消息变换为信号的措施
- 信道:指通信系统把载荷信息的信号从甲地传输到乙地的媒介或通道
- 译码器:译码将信道输出的编码信号 (已叠加了干扰) 进行反变换
- 信宿:消息传送的对象
2.2 信息论研究的目的
找到信息传输过程中的共同规律,以提高信息传输的可靠性、有效性、保密性和认证性,使信息传输系统达到最优化
- 可靠性:数字通信系统中可靠性用差错率/误码率来衡量,模拟通信系统的可靠性用信噪比来衡量
- 有效性:数字通信系统中有效性用频带利用率来衡量,模拟通信系统的有效性用有效带宽来衡量
3 其他
3.1 通信技术中的编码
5G 中使用了 LDPC 码作为长码块编码方案,使用 Polar 码 (极化码) 作为 5G eMBB 场景的控制信道编码方案
3G 标准中 (IMT-2000) Turbo 码作为其传输高速数据的信道编码标准