【LeetCode力扣】75 快速排序的子过程partition（荷兰国旗问题）-编程知识

【LeetCode力扣】75 快速排序的子过程partition（荷兰国旗问题）

1、题目介绍

2、解题思路

2.1、冒泡排序暴力破解

2.2、快速排序的子过程partition

2.2.1、详细过程描述

2.2.2、代码描述

1、题目介绍

原题链接：75. 颜色分类 - 力扣（LeetCode）

示例 1：

输入：nums = [2,0,2,1,1,0]

输出：[0,0,1,1,2,2]

示例 2：

输入：nums = [2,0,1]

输出：[0,1,2]

提示：

n == nums.length
1 <= n <= 300
nums[i] 为 0、1 或 2

2、解题思路

根据题目的意思，简单来说就是将数组里的数据按照0、1、2的顺序排列。

如果只是要求排序，其实投机取巧的方式很多，比如直接使用冒泡排序也能完成此题。

2.1、冒泡排序暴力破解

void sortColors(int* nums, int sz) {int i = 0;int j = 0;for (i = 0; i < sz - 1; i++){for (j = 0; j < sz - 1 - i; j++){if (nums[j] > nums[j + 1]){int tmp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tmp;}}}
}

冒泡排序：时间复杂度为O(n^2)，空间复杂度为O(1）

2.2、快速排序的子过程partition

但是根据题目的难度标识为中等，很明显这道题不是在考察冒泡排序的。

该题的难点在于如何原地遍历的情况下使得：时间复杂度为O(n)，空间复杂度为O(1)。即仅使用常数空间的一趟扫描算法。

而这里就用到了快速排序的子过程partition，partition能够通过一次遍历将所有元素按照标志数进行划分，小于放标志数左边，大于放标志数右边。

首先这里有个数组，规定小num的值放在左侧，大于num的值放在右侧，而等于num的值放在中间，下面进行partition过程讲解。

首先蓝色方框是小于num的区域，橙色方框是大于num的区域，i从0开始循环遍历。

规则：

当arr[ i ]小于num时，arr[ i ]与小于区域的下一个元素交换位置，然后小于区域向右移动一位，i++。
当arr[ i ]等于num时，i++。
当arr[ i ]大于num时，arr[ i ]与大于区域的上一个元素交换位置，然后大于区域向左移动一位，此时i不自增。

2.2.1、详细过程描述

首先arr[ i ] 等于3，小于5

【执行规则1】3与小于区域的下一位元素交换位置，而此时小于区域的下一个元素就是3，因此交换其实已经完成了。然后小于区域向右移动一位，i++。

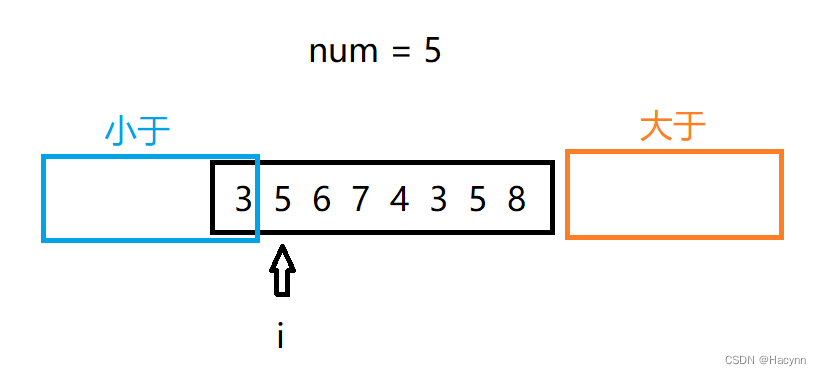
此时arr[ i ] 等于5

【执行规则2】直接 i++。

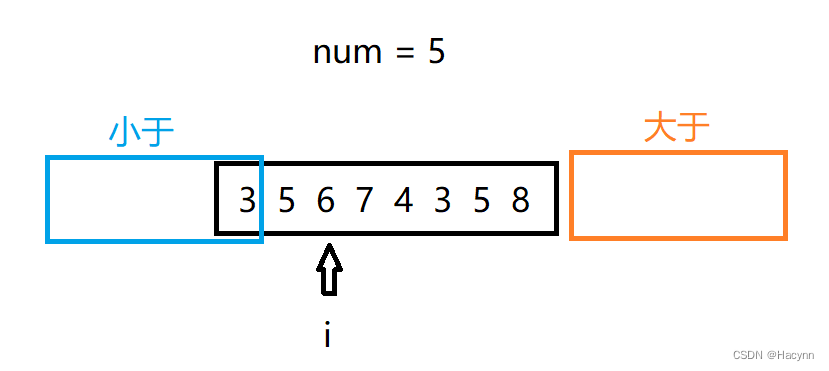
此时arr[ i ] 等于6，大于5

【执行规则3】3与大于区域的上一位元素交换位置，于是6和8交换位置。然后大于区域向左移动一位。

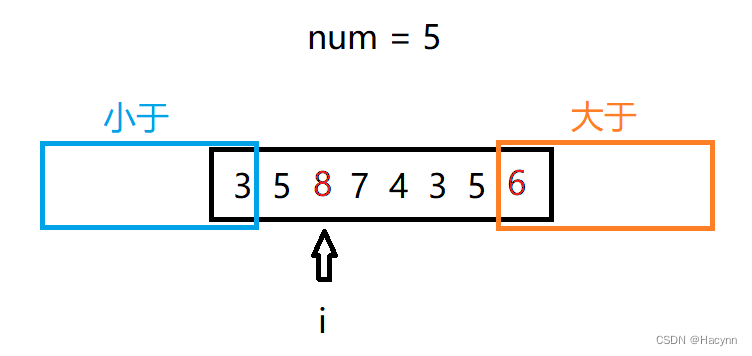
此时arr[ i ] 等于8，大于5

【执行规则3】8与大于区域的上一位元素交换位置，于是8和第二个5交换位置。然后大于区域向左移动一位。

此时arr[ i ] 等于5

【执行规则2】直接 i++。

此时arr[ i ] 等于7，大于5

【执行规则3】7与大于区域的上一位元素交换位置，于是7和第二个3交换位置。然后大于区域向左移动一位。

此时arr[ i ] 等于3，小于5

【执行规则1】3与小于区域的下一位元素交换位置，于是第一个5和第二个3交换位置。然后小于区域向右移动一位，i++。

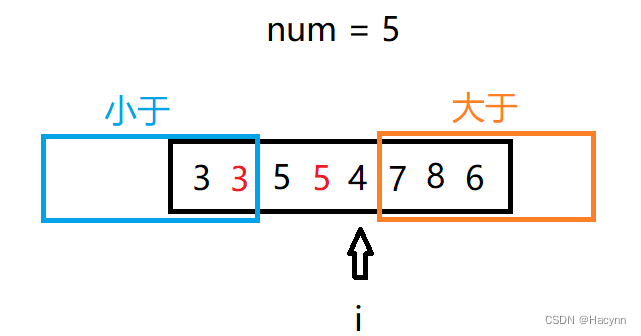
此时arr[ i ] 等于4，小于5

【执行规则1】4与小于区域的下一位元素交换位置，于是第一个5和4交换位置。然后小于区域向右移动一位，i++。

此时i遇到了大于区域了，就停止执行，此时数组中的值就变成了左边小右边大中间等于。

2.2.2、代码描述

按照快速排序的子过程partition的方法，改造代码，使标志数为1，然后将小于1的放左边，大于1的放右边，既完成排序。

void sortColors(int* nums, int numsSize){int signal  =  1;  //标志数int i = 0;int left = -1; //left为下标，是小于区域的右边界，刚开始还未进入数组，因此为-1int right = numsSize; //right为下标，是大于区域的左边界，刚开始还未进入数组，因此为numsSizewhile(i<right)   //当i遇上大于区域时停止循环，此时就完成了排序{if(nums[i] < signal)  //当nums[i]小于标志数{int tmp = nums[left+1];   //交换小于区域的下一个元素nums[left+1] = nums[i];nums[i] =  tmp;left++;i++;}else if(nums[i] > signal)  //当nums[i]大于标志数{int tmp = nums[right-1];  //交换大于区域的上一个元素nums[right-1] = nums[i];nums[i] = tmp;right--;}else{i++;   //等于时直接i++}}
}