有一个数字矩阵，矩阵的每行从左到右是递增的，矩阵从上到下是递增的，请编写程序在这样的矩阵中查找某个数字是否存在。

要求：时间复杂度小于O(N);

看到这个题目时，我们会马上想到暴力求解，即遍历这个矩阵的每一个元素，然而这种暴力求解方式的时间复杂度是O(N)，同时没有利用到杨氏矩阵的特点，那么有没有什么方法利用一下杨氏矩阵的特点呢？先看个杨氏矩阵的例子：

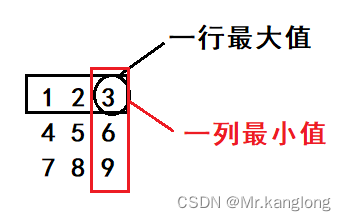
我们观察杨氏矩阵的特点，如果我们让待查找的数字（假设为5）和右上角的元素（3）比较，如果该元素比右上角元素大，那么这一行元素都不是我们要找的，因为这一行都比右上角元素小（1,2都比3小），那就可以跳过第一行，右上角元素变成6，继续和待查找的数字5比较，发现6比5大，那么6及其所在列（6 9）都比5大，那么可以排除6所在的列，右上角元素变成5，这样就查找到我们待查的元素5，以此类推。这样查到的次数肯定小于矩阵元素个数，满足时间复杂度的要求。

具体实现代码如下：

#include <stdio.h>
int find(int arr[3][3], int k,int* px,int* py)
{int x = 0;int y = *py - 1;while (x <= 2 && y >= 0){if (arr[x][y] < k){x++;}else if (arr[x][y] > k){y--;}else{*px = x;*py = y;return 1;//找到了，返回1}}return 0;//，没找到，返回0}int main()
{int arr[3][3] = { {1,2,3},{4,5,6},{7,8,9} };int k = 0;scanf("%d", &k);int x = 3;int y = 3;int ret = find(arr, k, &x, &y);if (ret == 1){printf("找到了,坐标是%d:%d\n",x,y);}else{printf("没找到\n");}return 0;
}

在这个代码中，还有一点值得我们学习一下，就是在find函数中，能够将查找值的坐标（2个数）同时返回出来，这是因为我们给find函数传入了x和y的地址。