前言
一道好题,也就花了我一个下午而已。
本人做法比较清奇,可以当做开阔思路参考,并不太建议实操(太难调了!)。
文章较啰嗦,谅解。
思路
众所周知,我并不太喜推式子,所以我们考虑直接根据题目限定的条件硬刚。
首先,我们先假定 1 1 1 为根,并求出每个点的子树的大小,记为数组 s i z e size size,并且再维护一下每一个点的时间戳。
接着我们考虑一种特殊情况,即如果 1 1 1 可以为树的重心的情况,那么他就会有接下来的两种子情况:
-
他所有的儿子的 s i z e size size 全部小于等于 n 2 \dfrac {n}{2} 2n。
-
有一个儿子 x x x 的 s i z e size size 大于 n 2 \dfrac {n}{2} 2n,且这个儿子的子树上一定能找到一个点 y y y 满足 s i z e x − s i z e y ≤ n 2 , s i z e y ≤ n 2 size_x-size_y \le \dfrac{n}{2},size_y\le \dfrac{n}{2} sizex−sizey≤2n,sizey≤2n。(把这个子树拆下来接到 1 1 1 上就可以满足重心的条件)
第二种情况不是很理解的话可以看下面这张图:
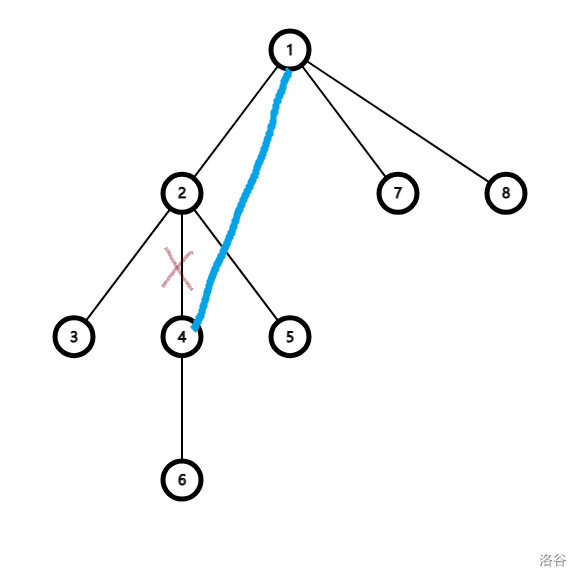
只有两种情况满足其一,那么 1 1 1 就可以成为树的重心。
接下来,我们迁移到一般的情况,那么就需要考虑除了他子树以外的情况。
对于树上的任意节点 x x x,要让他成为树的重心,就会有接下来的三种情况。
-
他所有的儿子的 s i z e size size 全部小于等于 n 2 \dfrac{n}{2} 2n,并且 n − s i z e x ≤ n 2 n-size_x \le \dfrac{n}{2} n−sizex≤2n。
-
同根节点的第二种情况。
-
n − s i z e x > n 2 n-size_x > \dfrac{n}{2} n−sizex>2n,即删除 x x x 后,不属于他子树的那一部分超过了重心的限制。那么在其中,我们又要分为两种情况。首先选择一个不在 x x x 子树上的点 y y y。如果 y y y 不在根节点到 x x x 的那条链上,那么只需要满足 s i z e y ≤ n 2 , n − s i z e x − s i z e y ≤ n 2 size_y \le \dfrac{n}{2},n-size_x-size_y\le \dfrac{n}{2} sizey≤2n,n−sizex−sizey≤2n。否则,我们拆下来的,就是除了 y y y 子树以外的部分,接到 x x x 上面去(毕竟你不可以把 x x x 的子树也拆下来,不然就会没有任何效果。),即满足条件 s i z e y − s i z e z ≤ n 2 , n − s i z e y ≤ n 2 size_y-size_z\le \dfrac{n}{2},n-size_y \le \dfrac{n}{2} sizey−sizez≤2n,n−sizey≤2n,只要找到一个符合条件的 y y y 即可。
那么接下来,问题就转化为了 x x x 能不能找到一个符合条件的 y y y。(毕竟第一个条件很好解决。)
接着继续转化问题,对于情况2,我们可以移一下项,将其转化为 y y y 满足条件 s i z e x − n 2 ≤ s i z e y ≤ n 2 size_x-\dfrac{n}{2} \le size_y \le \dfrac{n}{2} sizex−2n≤sizey≤2n,且 d f n x ≤ d f n y ≤ d f n x + s i z e x − 1 dfn_x \le dfn_y \le dfn_x+size_x-1 dfnx≤dfny≤dfnx+sizex−1。
对于情况三的第一种情况,我们也可以移一下项,转化为 n − s i z e x − n 2 ≤ s i z e y ≤ n 2 n-size_x-\dfrac{n}{2} \le size_y \le \dfrac{n}{2} n−sizex−2n≤sizey≤2n,且 d f n y < d f n x , d f n y > d f n x + s i z e x − 1 dfn_y<dfn_x,dfn_y>dfn_x+size_x-1 dfny<dfnx,dfny>dfnx+sizex−1(对于不在链上这一限制,后面会说怎么处理)。
这两种情况都可以看做有四个常数 p , q , l , r p,q,l,r p,q,l,r,判断是否有对于 x ∈ [ p , q ] , y ∈ [ l , r ] x \in [p,q],y \in [l,r] x∈[p,q],y∈[l,r] 存在 x = s i z e y x=size_y x=sizey。
显然,我们可以对于 s i z e size size 分块,然后开两个 s e t set set a , b a,b a,b, a x a_x ax (为什么用set后面会解释。)里面放所有 s i z e = x size=x size=x 的所有下标, b x b_x bx 放 s i z e size size 属于 x x x 这个块的所有的下标。最后查询时,以 s i z e size size 为第一维,对于散块,在 a a a 中二分,看有没有满足属于 [ l , r ] [l,r] [l,r] 的值,对于整块,则在 b b b 中二分。
接着,我们看向比较难处理的情况三的第二种情况。
我们可以动态维护一个数组,依次储存从根到该节点的链上的所有 s i z e size size 值,可以发现是单调递减。并且记得在加入数组时,删除他在 a , b a,b a,b 中的值,在删除数组元素时,加回去。(因为必须要保证在情况三的情况1解决时要不包含这些在链上的元素)。这里的删除和加入就解释了为什么要采用 set。接着可以先在数组中二分找出满足 n − s i z e y ≤ n 2 n-size_y \le \dfrac{n}{2} n−sizey≤2n 的 y y y 的范围,然后在这个范围中继续二分找出是否存在满足 s i z e y − s i z e z ≤ n 2 size_y-size_z\le \dfrac{n}{2} sizey−sizez≤2n 的 y y y,那么就解决了情况3的第二种情况。
时间复杂度,分块+二分,及 n n log n n \sqrt n \log n nnlogn,但因为二分的区间长度不可能每次都是顶着的,所以远远达不到这个上界,但仍然很慢。
所以问题就 迎刃而解 了!
代码
#include<bits/stdc++.h>
using namespace std;
int n;
struct node
{int tar,nxt;
}arr[800005];
int fst[400005],cnt;
void adds(int x,int y)
{arr[++cnt].tar=y,arr[cnt].nxt=fst[x],fst[x]=cnt;
}
int size[400005],dfn[400005],tot,rnk[400005];
int klen,len;
set<int> a[400005],b[100005];
bool dp[400005];
void dfs(int x,int last)
{dfn[x]=++tot;rnk[dfn[x]]=x;for(int i=fst[x];i;i=arr[i].nxt){int j=arr[i].tar;if(j==last) continue;dfs(j,x);size[dfn[x]]+=size[dfn[j]];} size[dfn[x]]++;
}
int getk(int x)
{return ceil(x/(klen*1.0));
}
int lk(int x)
{
// cout<<x<<" "<<(x-1)*klen+1<<endl;return (x-1)*klen+1;
}
int rk(int x)
{if(x==len) return n;else return x*klen;
}
bool ch1(int p,int x,int y)
{
// cout<<p<<" "<<x<<" "<<y<<endl;set<int>::iterator q=a[p].lower_bound(x);if(q==a[p].end()) return false;else if(*q<=y) return true;else return false;
}
bool ch2(int p,int x,int y)
{set<int>::iterator q=b[p].lower_bound(x);if(q==b[p].end()) return false;else if(*q<=y) return true;else return false;
}
bool check(int l,int r,int x,int y)
{
// cout<<l<<" "<<r<<" "<<x<<" "<<y<<endl;if(l>r) return false;int p=getk(x)+1,q=getk(y)-1;int pp=rk(getk(x)),qq=lk(getk(y));if(p>q){for(int i=x;i<=y;++i) if(ch1(i,l,r)) return true;}else{for(int i=x;i<=pp;++i) if(ch1(i,l,r)) return true;for(int i=qq;i<=y;++i) if(ch1(i,l,r)) return true;for(int i=p;i<=q;++i) if(ch2(i,l,r)) return true;}return false;
}
int p[400005],tail=400001;
void add(int x)
{p[--tail]=size[dfn[x]];x=dfn[x];set<int>::iterator q=a[size[x]].lower_bound(x);a[size[x]].erase(q);q=b[getk(size[x])].lower_bound(x);b[getk(size[x])].erase(q);
}
void del(int x)
{tail++;x=dfn[x];a[size[x]].insert(x);b[getk(size[x])].insert(x);
}
void get_ans(int x,int last)
{if(x!=1)add(x);int flg=0,num=0,l,r;bool bj=0;for(int i=fst[x];i;i=arr[i].nxt){int j=arr[i].tar;if(j==last) continue;if(size[dfn[j]]>n/2) flg++,num=size[dfn[j]],l=dfn[j],r=dfn[j]+size[dfn[j]]-1;get_ans(j,x);}del(x);if(n-size[dfn[x]]>n/2) flg++,num=n-size[dfn[x]],bj=1;if(flg>=2) return;if(flg==0){dp[x]=1;return;}if(!bj){if(check(l,r,num-n/2,n/2))dp[x]=1;}else{ //x,x+size[x]-1if(check(1,dfn[x]-1,num-n/2,n/2)||check(dfn[x]+size[dfn[x]],n,num-n/2,n/2))dp[x]=1;if(dp[x]){return;}
// cout<<x<<" "<<1<<endl;int ll=lower_bound(p+tail,p+400000+1,n-n/2)-p,rr=400000,mid,ans;while(ll<=rr){mid=(ll+rr)>>1;if(p[mid]-size[dfn[x]]<=n/2){dp[x]=1;break;}else{rr=mid-1;}}}
}
int main()
{scanf("%d",&n);for(int i=1;i<n;++i){int x,y;scanf("%d%d",&x,&y);adds(x,y);adds(y,x);}klen=sqrt(n),len;if(klen*klen==n) len=klen;else len=klen+1;dfs(1,0);for(int i=1;i<=n;++i) a[size[i]].insert(i),b[getk(size[i])].insert(i);get_ans(1,0);for(int i=1;i<=n;++i) printf("%d ",dp[i]);
}
暴力出奇迹!!!!!
T h e E n d \Huge\mathscr{The\ End} The End