在实际使用softmax计算loss时,有一些关键地方与具体用法需要注意:
交叉熵是十分常用的,且在TensorFlow中被封装成了多个版本。多版本中,有的公式里直接带了交叉熵,有的需要自己单独手写公式求出。如果区分不清楚,在构建模型时,一旦出现问题将很难分析是模型的问题还是交叉熵的使用问题。
示例代码如下:
import tensorflow as tf#labels和logits的shape一样
#定义one-hot标签数据
labels = [[0,0,1],[0,1,0]]
#定义预测数据
logits = [[2,0.5,6],[0.1,0,3]]#对预测数据求一次softmax值
logits_scaled = tf.nn.softmax(logits)
#在求交叉熵的基础上求第二次的softmax值
logits_scaled2 = tf.nn.softmax(logits_scaled)#使用API求交叉熵
#对预测数据与标签数据计算交叉熵
result1 = tf.nn.softmax_cross_entropy_with_logits(labels = labels, logits = logits)#对第一次的softmax值与标签数据计算交叉熵
result2 = tf.nn.softmax_cross_entropy_with_logits(labels = labels, logits = logits_scaled)
result3 = tf.nn.softmax_cross_entropy_with_logits(labels = labels, logits = logits_scaled2)#使用公式求交叉熵
result4 = -tf.reduce_sum(labels*tf.compat.v1.log(logits_scaled),1)#标签数据各元素的总和为1
labels2 = [[0.4,0.1,0.5],[0.3,0.6,0.1]]
result5 = tf.nn.softmax_cross_entropy_with_logits(labels = labels2, logits = logits)#非one-hot标签
labels3 = [2,1]#等价于labels3==[tf.argmax(label,0),tf.argmax(label,1)]
#使用sparse交叉熵函数计算
result6 = tf.nn.sparse_softmax_cross_entropy_with_logits(labels = labels3, logits = logits)print("logits_scaled=",logits_scaled)
print("logits_scaled2=",logits_scaled2)
print("result1=",result1)
print("result2=",result2)
print("result3=",result3)
print("result4=",result4)
print("result5=",result5)
print("result6=",result6)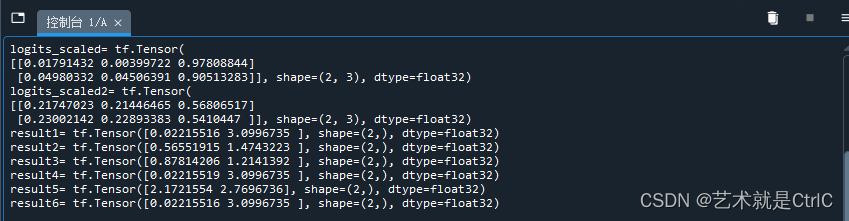
总结:
使用softmax交叉熵函数计算损失值时,如果传入的实参logits是神经网络前向传播完成后的计算结果,则不需要对logits应用softmax算法,因为softmax交叉熵函数会自带计算softmax
使用sparse交叉熵函数计算损失值时,样本真实值与预测结果不需要one-hot编码,传给参数labels的是标签数数组中元素值为1的位置
由于交叉熵的损失函数只和分类正确的预测结果有关系,因此交叉熵的计算适用于分类问题上,不适用于回归问题。而均方差(MES)的损失函数由于对每一个输出结果都非常重视,不仅让正确的预测结果变大,还让错误的分类变得平均,更适用于回归问题,不适用于分类问题
当使用Sigmoid作为激活函数的时候,常用交叉熵损失函数而不是均方差(MES)损失函数,以避免均方差损失函数学习速率降低的问题。