挑战极限一天打三场比赛失败,困得要死。
D
你说得对,但为什么我的树形dp式子那么复杂?
考虑如果要调整\(a_u\)与\(a_{fa_u}\)相等,仅仅是操作\((u,fa_u)\)或\((fa_u,u)\)有意义(保证不影响其他节点的差)
所以对于每个\((u,fa_u)\),至少需要调整\(|a_u-a_{fa_u}|\)次。
剩下的就是简单dp了,不说了。
E1
昨天的状态使我就算策略让我先看E1我也不会去看......
考虑肯定要找到一个子树,删除根\(u\)后剩下的大于\(a_u\)的值存在。
考虑怎么选是最优的,对于当前选择的w\(,若\)u,v,w\(分居子树并且\)a_u>a_v>a_w\(,那么选择\)v\(一定更优。
意思就是,我们要选择符合条件的子树时,同时保证\)a_u$最大。
Codeforces Round 1001,Div. 1 + Div. 2记录
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/876209.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
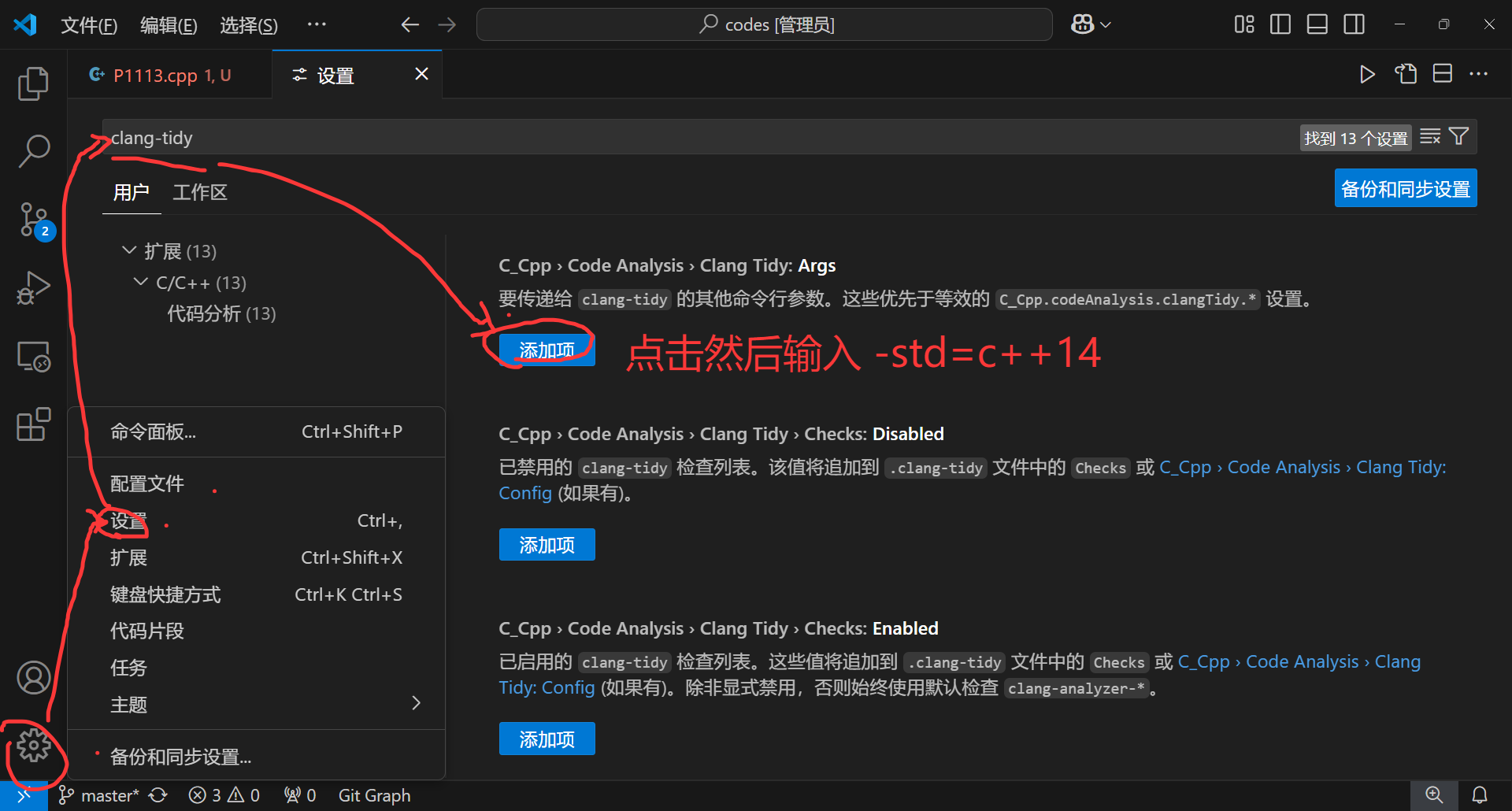
VS Code 报错 __float128 is not supported on this target 解决方法
最近在使用 VS Code 时,每一个 cpp 文件都会有如下报错:在中文互联网上并没有搜索到很好的解决方案,但是在 stack overflow 上找到了一个比较好的回答:This problem may be caused by your VSCode using clang-tidy as the C/C++ extension. clang-tidy does not support _…
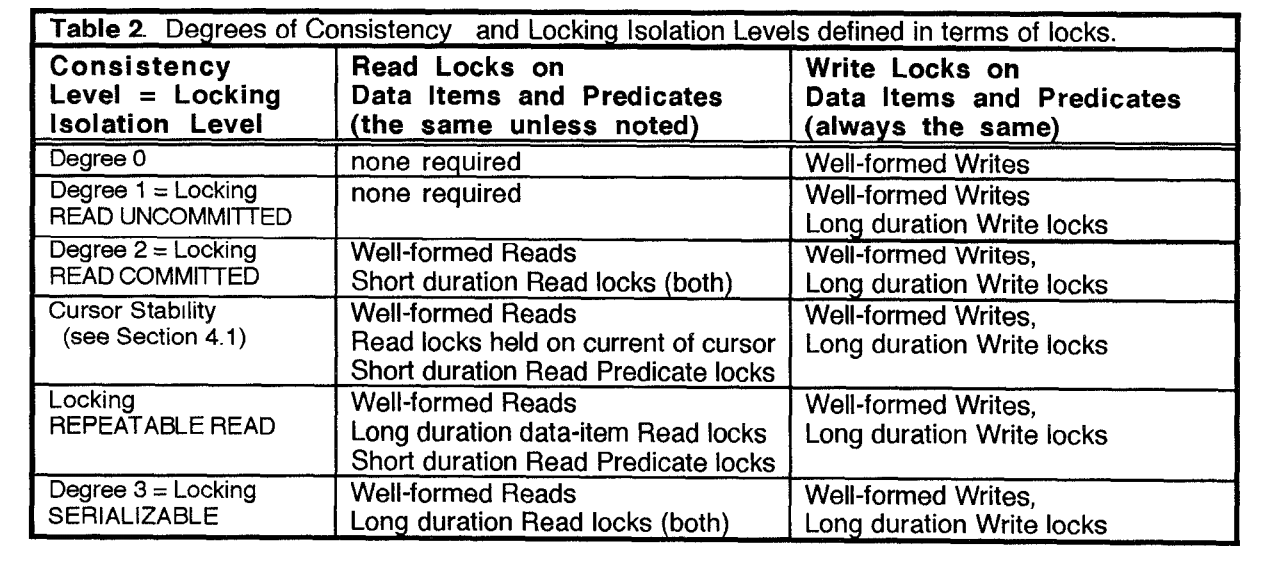
A Critique of ANSI SQL Isolation Levels.18687395
原文:A critique of ANSI SQL isolation levels摘要:ANSI SQL-92[MS, ANSI]使用脏读、不可重复读以及幻读现象(phenomena)定义了隔离级,本论文展示了这些现象,以及ANSI SQL定义并无法合适的描述众多流行的隔离级别,包括(ANSI标准)所涵盖的级别的标准锁实现。我们还介绍…
0127人工智能创新型教师培育计划(第一期) 试题
# 试题
http://site01.openhydra.net:30012/evt/uploadcode人工智能创新型教师培育计划(第一期)
【活动进展每日更新1月26日】活动更新(1月26日 22:00更新):
Python作业教师AI基础考核作业(见下面介绍),或者可以下载word文件 查看。
1月31日中午24:00前提交,
作…
.net core 使用账号密码方式读取SharePoint 文件(记录)
项目环境 .net 6.0 原代码 是.netframework 4.6
原代码引用了Microsoft.SharePoint.Client 包去操作.其中身份验证的使用的是 SharePointOnlineCredentials 类.但迁移到.net 6,0 后发现这个类已经被移除.测试了常用 的各种方式,大部分均返回403
解决方案: 使用包 dotnet add…
mkcert生成ssl证书+nginx部署局域网内的https服务访问
环境
使用的是树莓派 安装的是ubuntu 系统
https://github.com/FiloSottile/mkcert/releases 下载
添加权限
chmod 777 ./mkcert-v1.4.4-linux-arm64
1、CA 证书加入本地可信 CA
./mkcert-v1.4.4-linux-arm64 -install
2、生成自签证书
./mkcert-v1.4.4-linux-arm64 …
iPhone 拍摄 LED 灯带视频时候如何防频闪 All In One
iPhone 拍摄 LED 灯带视频时候如何防频闪 All In One
闪动频率不一致 bug?
60Hz
50HziPhone 拍摄 LED 灯带视频时候如何防频闪 All In One闪动频率不一致 bug?60Hz
50Hz
errorshttps://www.bilibili.com/video/BV1F5fkY6ERS/
问题分析
灯的问题,灯在闪。
交流电是 50Hz(中国…
iPhone 视频拍摄 LED 灯带时候如何防频闪 All In One
iPhone 视频拍摄 LED 灯带时候如何防频闪 All In One
闪动频率不一致 bug?
60Hz
50HziPhone 视频拍摄 LED 灯带时候如何防频闪 All In One闪动频率不一致 bug?60Hz
50Hz
errorshttps://www.bilibili.com/video/BV1F5fkY6ERS/
solutions
demos(🐞 反爬虫测试!打击盗版⚠️)…
AI智能体(Agent)总体框架及技术发展现状
智能体(Agent)定义
AI智能体,又称AI代理或 Al Agent,是能够感知环境,基于目标进行决策并执行动作的智能化应用。它具备自主性、交互性、反应性和适应性等基本特征,能够在复杂多变的环境中独立完成任务。智能体的出现,标志着人工智能从简单的规则匹配和计算模拟向更高级别的…
记忆层以前所未有的方式增强了LLMs
深入探讨记忆层如何工作,以及它们如何增强LLMs,以至于下一代AI架构如果不采用它们,将会错失良机。图像由DALL-E 3生成LLMs(大型语言模型)是存储在其参数中的庞大信息知识库(主要是以密集层中线性矩阵变换的权重形式存在)。
然而,随着参数规模的增长,计算成本和能源消耗…
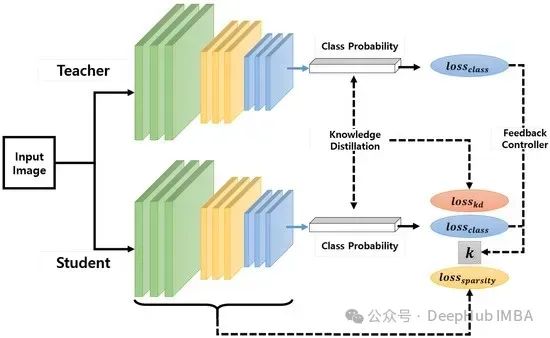
知识蒸馏技术原理详解:从软标签到模型压缩的实现机制
知识蒸馏是一种通过性能与模型规模的权衡来实现模型压缩的技术。其核心思想是将较大规模模型(称为教师模型)中的知识迁移到规模较小的模型(称为学生模型)中。本文将深入探讨知识迁移的具体实现机制。知识蒸馏原理
知识蒸馏的核心目标是实现从教师模型到学生模型的知识迁移。…
GIS数据合集:作物、植被数据下载平台整理
本文对目前主要的作物类型与产量、植被物候与指数数据产品的获取网站加以整理与介绍~本文对目前主要的作物类型与产量、植被物候与指数数据产品的获取网站加以整理与介绍。
目录4 植被农业数据4.1 作物产量数据4.1.1 SPAM4.1.2 Aerial Intelligence4.2 作物物候数据4.2.1 China…