哈希函数是怎么构成的?
Merkle–Damgård结构
- 哈希函数需要能够处理任意长度的输入。
- 许多散列函数,例如MD5、SHA-1、SHA-2,都是由构建块(称为压缩函数)组成的,这些构建块可以处理特定的块大小,并提供较短的输出,例如SHA-256:768位到256位
- 输入被分解成块,并用1000…0填充,连接64位的输入长度
- 如果h是抗冲突的,则哈希函数是抗冲突

如果压缩函数本身是抗碰撞的,那么我们可以证明Merkle–Damgård结构是抗碰撞的。这样一来,输入长度不固定的哈希函数的安全性就简化为输入长度固定的压缩函数的安全性。
Davies–Meyer结构
- 给定一个分组密码,构造一个压缩函数
- 消息块作为分组密码密钥
- 以前的散列块作为分组密码输入
- 从分组密码的密钥+分组长度到分组密码的分组长度的压缩
- 如果分组密码是“理想”的分组密码,则该结构是抗冲突的
- 用于MD5(损坏)、SHA-1(E=SHACAL-1)、SHA-2(E=SHACAL-2)
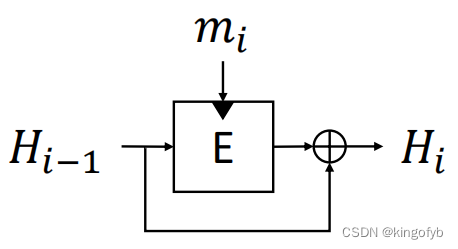
这个压缩函数的第一个输入块作为分组密码的密钥;第二个输入块作为分组密码的输入进行加密。然后,用第二个输入快与分组密码的输出进行异或操作。
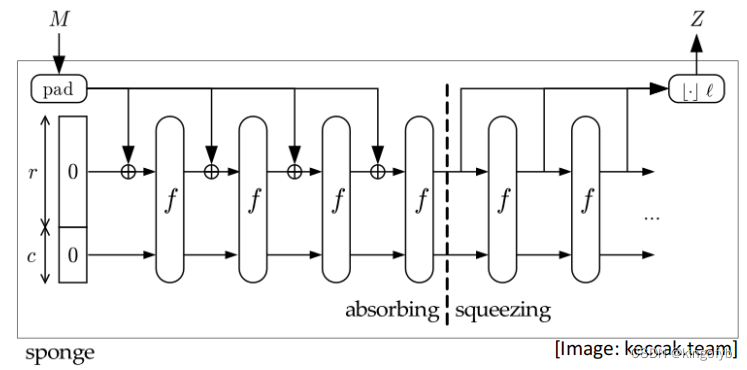
Sponge Construction - 海绵结构
- 最近的散列函数,比如SHA-3(Keccak),是基于一个叫做Sponge的构造。
- 安全级别由容量c决定,r表示速率。
- 与Merkle–Damgård不同,Sponge的输出大小是灵活的。
注:这三个构造只是简单介绍了一下,并没有详细的解释原理。以后有时间会把每个构造单独写一篇博客。
SHA-3 竞赛
- 目标:替代SHA-2
- 2007年:NIST宣布竞争
- 2008年:提交截止日期,宣布了51名第一轮候选人
- 2009年:宣布了14名第二轮候选人
- 2010年:宣布了5名决赛选手:BLAKE、Grøstl、JH、Keccak、Skein
- 2012年:Keccak宣布成为SHA-3冠军
Z
https://csrc.nist.gov/projects/hash-functions/sha-3-project
https://ehash.iaik.tugraz.at/wiki/The_SHA-3_Zoo
一个好的哈希函数能带来多强的安全性
Preimage Security - 第一原像性安全
- 如果我们有一个完美的散列函数,比如说256位输出…
- 执行图像前攻击(即给定输出,找到输入)的唯一方法是尝试逐一对不同输入进行彻底搜索(也称为暴力搜索 - brute-force)。
- 我们很有可能通过尝试大约2256个输入来找到预图像(为什么?)。所以我们说它提供了256位的预映像安全性。
- 具有d位输出的哈希函数可能提供的最大预映像安全级别是d位。
Collision Security - 碰撞性安全
- 让我们在具有256位输出的哈希函数中强制执行冲突
- •当我们尝试例如第i个输入时
, 我们可以检查一下𝐻(
) 与之前的任何一个相同,比如𝐻(
),𝐻(
),...,𝐻(
)
- 因此,在第i步中,我们有成功的概率𝑖/
- 所以总的概率是:
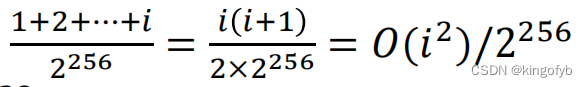
- 这意味着,通过大约
次尝试,我们可以很有可能发现碰撞
- 具有d位输出的哈希函数可能提供的最大冲突安全级别为d/2位
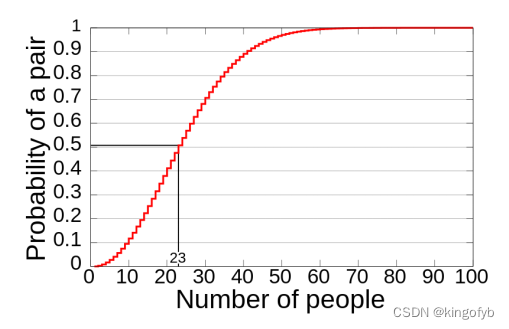
Birthday Bound - 生日边界
- 对于很多人来说,找到一对生日相同的情侣的概率是多少?
- 只有23人,约50%的机会
- 一般来说,如果有𝑛个可能性,随机选择将有50%的机会碰撞后大致
尝试。
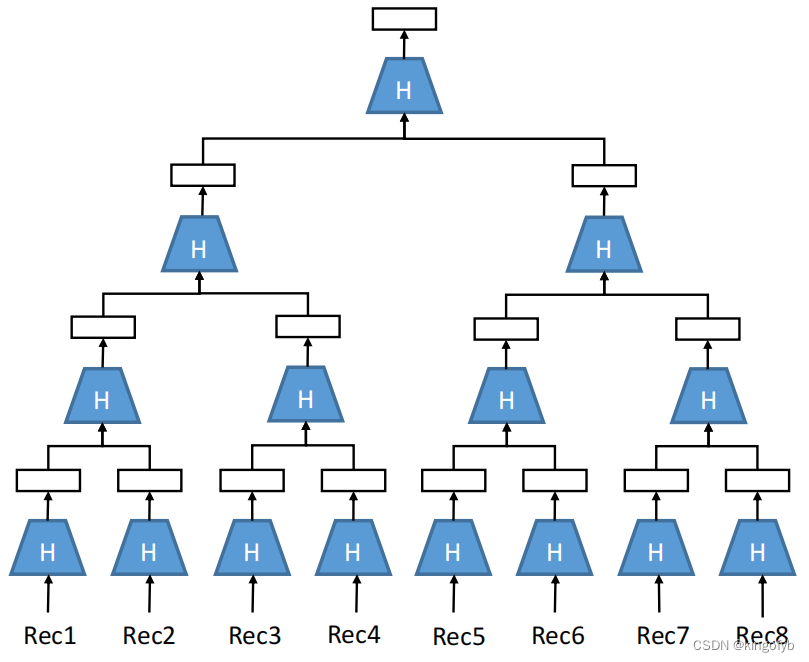
Merkle哈希树
- 哈希可以排列在一个称为Merkle哈希树的二叉树中。
- 只有最高级哈希(根哈希)才需要保持安全,以检测记录中的任何更改。
- 用于例如BitTorrent、Git、比特币
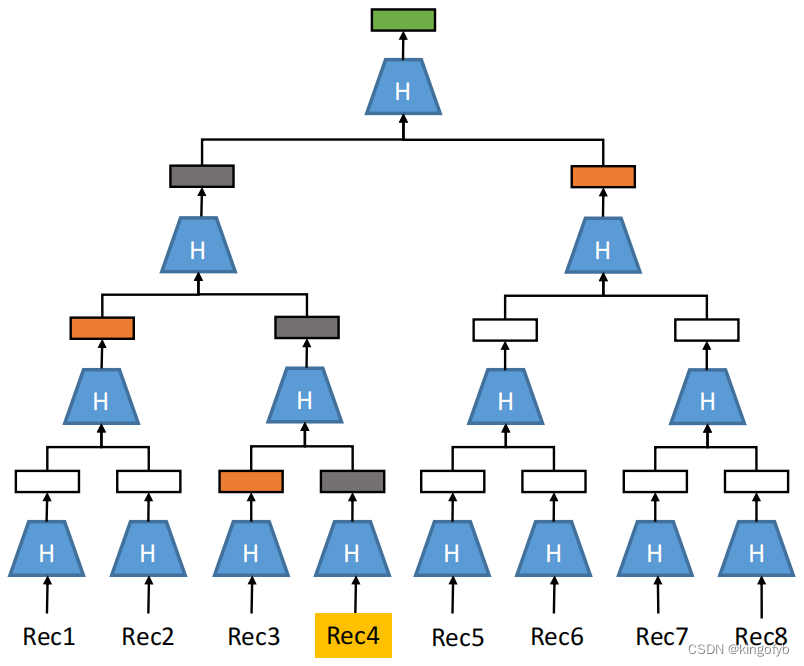
Membership Proof
- 为了证明记录在数据库中具有给定的根哈希,只需要给定与路由到根哈希相邻的哈希。
- 其余数据不需要,可以保持隐私。
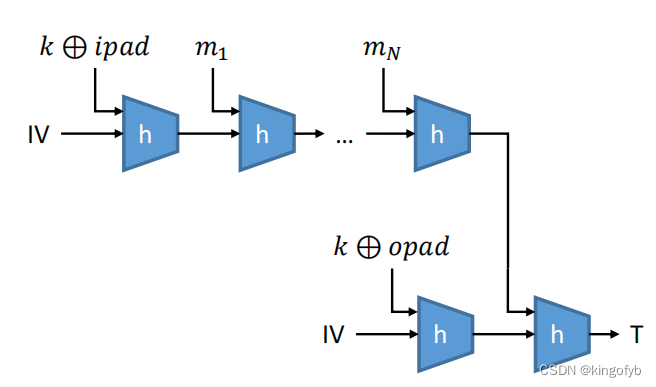
HMAC
- 修改Merkle–Damgård结构,从压缩函数h构建安全的MAC
- ipad和opad是固定常数
- 如果h具有抗碰撞性,则HMAC为UF-CMA
- 比CBC-MAC快得多