提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

最优化是应用数学的一个分支，主要研究在特地情况下函数的最大最小值。
优化目标一般有凸函数和非凸函数两种。其中凸函数的全局最小值与局部最小值一般重合。其中非凸函数的局部最小值点有很多，不与凸函数的全局最小值点重合。
在深度学习中，由于激活函数的非线性特点和网络的复杂性，导致要优化的目标是一个很复杂的非凸函数。
在深度学习中的优化方法一般可以分为两类
第一类是 基于更新方向（SGD，Momentum）
第二类是 基于选择更适合的学习率（）

---

一、SGD（随机梯度下降算法）

假设目标函数为

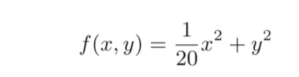
该函数的图像以及等高线图

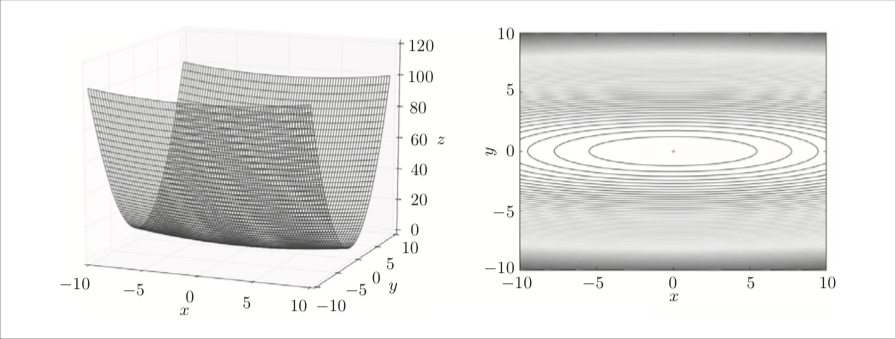
首先一个目标函数的梯度指的是垂直于等高线的切线，并且朝着这个方向，目标函数值上升最快。

所以随机梯度下降算法就是，不断的更新参数的梯度，更新的方向是朝着这个方向，目标函数值下降最快。更新的值与步长有关。

W = W - 步长*梯度

使用随机梯度下降算法的更新路径如下：

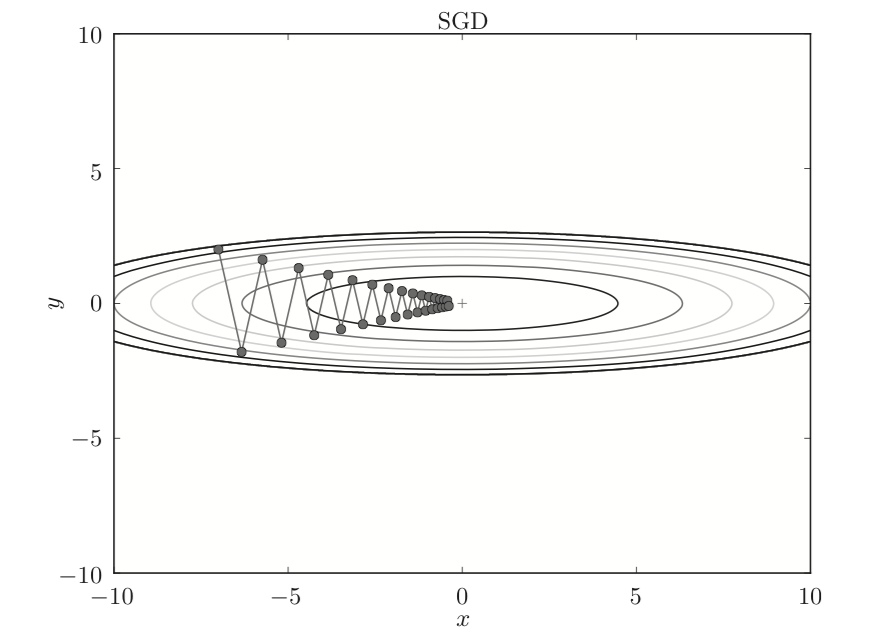
随机梯度下降算法的特点就是实现简单，但是效率不高

二、Momentum

Momentum的公式如下：

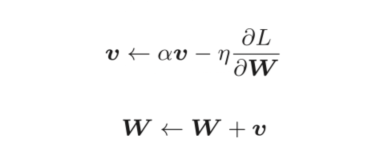
在更新梯度时。有一个V向量，如何理解这个向量对更新梯度的影响呢？观察下图。

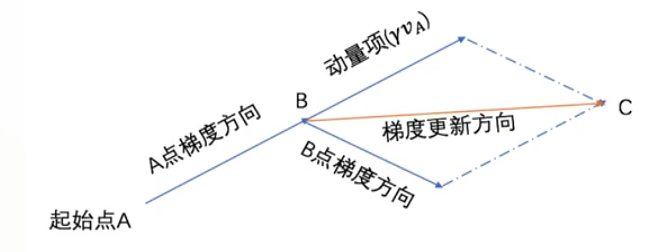
在B点，V向量的方向是B点的上一个点A点的梯度更新方向，而此时B点梯度方向如图，如果是SGD算法，整个目标函数会朝着B点的梯度方向去更新，如果是加入V向量的话，会朝着A点的梯度更新方向与B点的梯度更新方向中间方向取更新梯度。这样做的好处
更新的会更快，效率更高，不会像SGD那样拐来拐去。

使用momentum的更新路径如下：

---

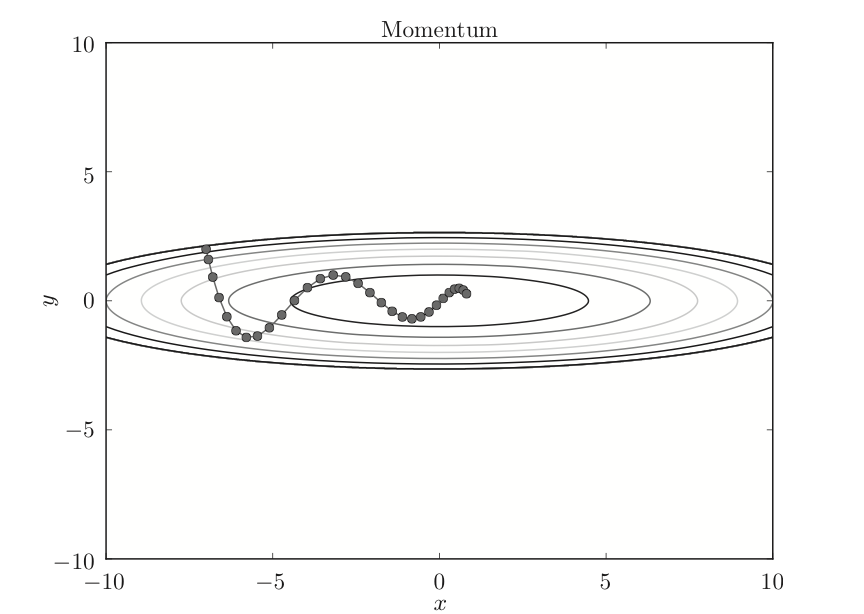
三、AdaGrad

接下来介绍的都属于第二类，主要是如果更新学习率（步长）。有一种被称为学习率衰减的方法，即是随着学习的进行，使学习率逐渐减小。

AdaGrad会为每一个元素适当的调整学习率，AdaGrad的更新方法如下：

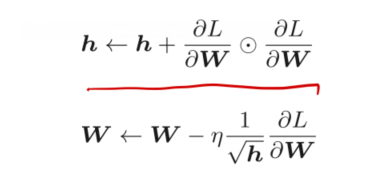
h代表的是累积以前所有参数的梯度平方和，在更新参数时，通过乘以1/根号h，就可以使得，如果参数的梯度值变化较大，那么对应的该参数的学习率会逐渐减小。
更新的路径如下：

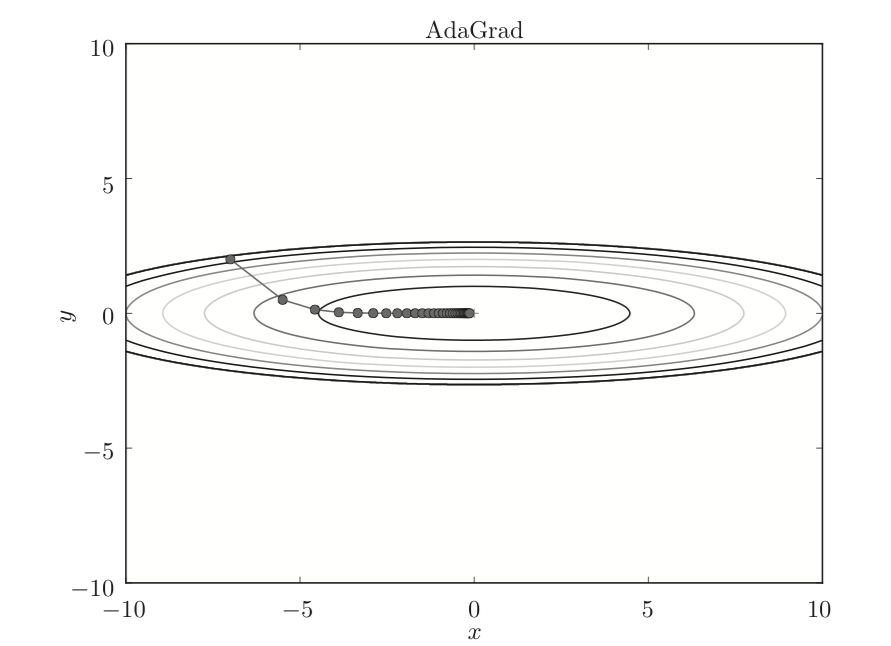
当然这个算法存在一定问题，就是如果训练次数很多，h一直累加，就会导致h趋于无穷，1/h则趋于0，就会导致参数无法更新。针对这个问题，提出RMSprop算法。RMSprop的思想就是，加入了衰减因子，使得当前的梯度对步长的影响更大，而之前累加的梯度和对步长的影响相比之下更小。公式如下：

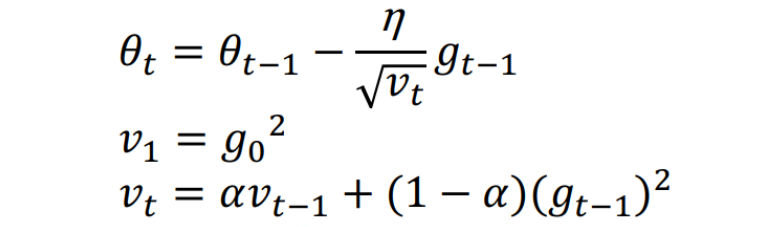
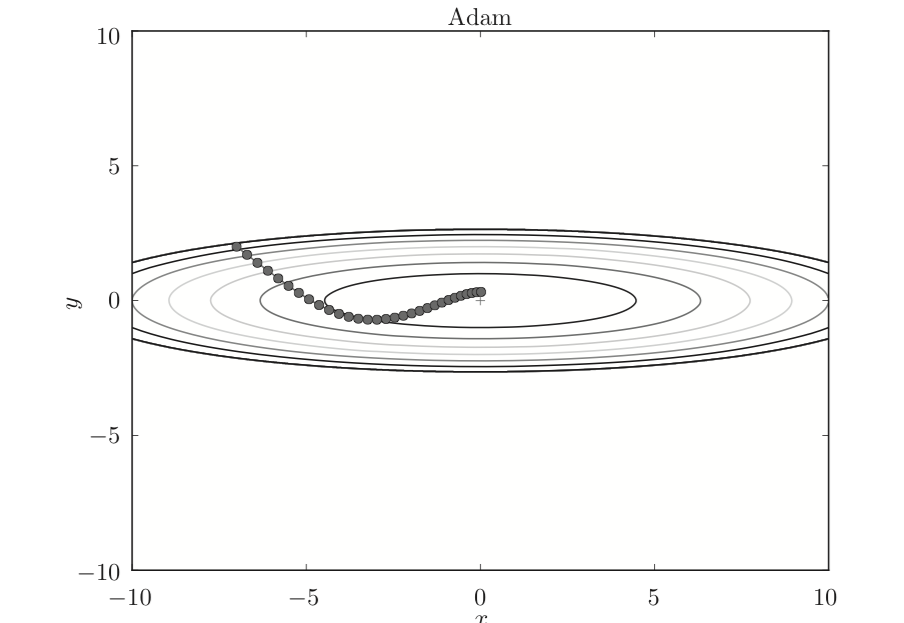
四、Adam算法

Adam算法就是融合Momentum和AdaGrad这两种方法。即对参数梯度更新的方向进行了优化，又对学习率进行优化。
使用Adam的更新路径如下：