一、实验目的
利用回溯法搜索或爬山法找到八皇后问题的一个可行解。
二、实验内容
有一个 8 × 8 的棋盘,现在要将8个皇后放到棋盘上,满足:对于每一个皇后,在
自己所在的行、列、两个对角线都没有其他皇后。求所有满足的摆放方式。

图2-1 八皇后问题示意图
三、实验方法
(A)爬山法:
经典的爬山算法也称为局部贪婪搜索(Greedy Local Search),其在算法层的原理为:
随机生成初始状态;
探索初始状态的邻域 K,在 K中选择代价最小(或价值最高)的状态;
若此状态代价小于当前,则选择此状态为下一个状态;否则算法停止;
重复(ii)(iii)直至最优或算法停止。
思路:
1. 先初始化皇后位置,使得每一行每一列一个有且仅有一个皇后
2. 计算冲突的皇后数量(计做冲突值),比如同一行、同一列、同一斜线的数量
3. 准备移动皇后,但是往哪移动呢?每一行皇后只能在自己所在行移动,所以只有列会改变
比如把第一行皇后从(0,1)移动到(0,0),那么整个棋局的冲突值会发生改变(假设冲突值变小了6->5),此时记录为(0,0):5
然后遍历所有空位,记录移动到此空位时所有皇后的对应冲突值
4. 找到棋盘中所有空位的冲突值最小的位置,随机选择一个冲突值最小空位置,移动所在行皇后此位置,然后重复上一步3的动作,重新计算棋盘上所有皇后冲突值和所有空位冲突值,循环动作3,直到所有皇后的冲突值为0,此时已经找到一组正确的8皇后位置
5.到第四步已经完成了爬山算法,但是爬山算法有个缺点,有可能找到局部最优,而不是全局最优
以本案为例只找到了一组最佳位置,但事实上有很多组。此时可以随机生成多个初始位置(也就是爬山起点分散多个地方),就可以找到不同的最佳答案了。

图3-1 爬山法运行结果截图
| import random, copy, time """ 解决8皇后问题 初始化 随机生成皇后位置,使其不同列、不同行只有一个 """ def init(): # 随机生成皇后位置,使其不同列、不同行只有一个 status = [] for r in range(8): while len(status) <= 8: c = random.randint(0, 7) if c not in [mm[1] for mm in status]: status.append((r, c)) break return status """ 遍历所有皇后 计算有冲突的皇后坐标(同一行,同一列,斜边) 计算整个棋盘冲突的数量 假设初始化传入皇后位置: [(0, 3), (1, 6), (2, 7), (3, 0), (4, 2), (5, 1), (6, 4), (7, 5)] """ def conflict(status): num = 0 # 存储冲突数量 conflict_chess = [] for pos in status: for other_pos in status: if pos == other_pos or pos in conflict_chess: continue elif pos[0] == other_pos[0] or pos[1] == other_pos[1] or abs(pos[0] - other_pos[0]) == abs( pos[1] - other_pos[1]): num += 1 conflict_chess.append(pos) return num, conflict_chess """ 遍历所有空位 计算当行的皇后移动到此空位时整个棋盘的冲突值 会得出8*8-8 = 56个冲突值 也就是56种移动方法 选择冲突值最小的一种进行移动 """ def move_chess(status): empty_pos = {} # 用字典保存所有空位冲突值 for r in range(8): for c in range(8): if (r, c) not in status: new_status = copy.deepcopy(status) new_status[r] = (r, c) empty_pos[(r, c)] = conflict(new_status)[0] else: continue return empty_pos """ 循环获取冲突数量 若数量>1,执行move_chess 指导冲突数量=0,此时寻找到最佳位置 """ def climbing(status): # 获取当前皇后位置的冲突值 conflict_num = conflict(status)[0] # 设置循环次数,避免一直循环,冲突值一直无法降到最低0时,自动跳出循环 # 设置移动皇后500次,如果找不到正确位置就重新初始化皇后位置 loop_cnt = 0 while conflict_num != 0 and loop_cnt < 500: # 获取所有空位冲突值 empty_pos = move_chess(status) min_value = min(empty_pos.values()) # 获取最小冲突值对应的key 即坐标pos min_pos_ls = [] for k, v in empty_pos.items(): # print(v, min_value) if v == min_value and (k not in min_pos_ls): min_pos_ls.append(k) # print(min_pos_ls, min_value) # print(status) # 随机取一个空位点,与当前同一行皇后交换位置,然后计算所有空位置的冲突值和当前棋局内皇后自身冲突值 i = random.randint(0, len(min_pos_ls) - 1) status[min_pos_ls[i][0]] = min_pos_ls[i] conflict_num = conflict(status)[0] loop_cnt += 1 return status, loop_cnt if __name__ == '__main__': # 这一个随机数会导致一直找不到最高点 # status = [(0, 0), (1, 2), (2, 4), (3, 3), (4, 1), (5, 5), (6, 7), (7, 6)] # climbing(status) """ 生成随机位置,迭代600次尽可能多的找出八皇后不同位置 """ start = time.time() all_pos = [] for i in range(600): status = init() # 设置loop_cnt防止一直陷入死循环无法找到最佳点 # 如果一直找不到就跳出来并且重新生成初始位置 status, loop_cnt = climbing(status) # print(loop_cnt) if loop_cnt == 500: continue elif status not in all_pos: all_pos.append(status) end = time.time() print("一共找到{}组八皇后位置,共耗时{}s".format(len(all_pos), end - start)) for pos in all_pos: print(pos) |
回溯法:
- Queen_set 函数接受一个参数 n,表示已经放置的皇后数量。
- queen_col_loc 列表用于存储皇后的列位置。
- 如果 n 等于 8,表示已经成功放置了八个皇后。在这种情况下,函数通过显示皇后的位置来打印解决方案。
- 调用 plot_chess 函数绘制当前的皇后摆放方案。
- 递增方案数 num 的值。
- 返回函数。
- 否则,循环遍历当前行的每个位置。
- 检查当前位置是否可以放置皇后,调用 check 函数进行检测。
- 如果可以放置皇后,将当前位置添加到 queen_list 列表中。
- 递归调用 Queen_set 函数放置下一个皇后。
- 回溯,尝试当前行的其他皇后摆放方法,从 queen_list 列表中移除最后一个元素。
- check 函数用于检测皇后的位置是否合法。
- 如果是第一行,直接返回 True。
- 否则,循环遍历之前的每一行。
- 检查当前位置是否与之前的皇后所在的列有冲突。
- 检查当前位置是否与之前的皇后所在的主对角线和副对角线有冲突。
- 如果有任何冲突,返回 False。
- 如果通过了所有检测,返回 True。
- plot_chess 函数用于绘制棋盘并保存求解结果。
- 创建一个大小为 8x8 的全零数组 map。
- 遍历每一行,将皇后所在的列位置设为 1。
- 创建一个颜色映射 cmap,用于绘制棋盘。
- 使用 plt.imshow 函数绘制棋盘。
- 设置标题和刻度。
- 保存绘制的棋盘图像。
- 初始化 queen_list 列表为空。
- 初始化当前方案数 num 为 1。
- 调用 Queen_set 函数,从第一行开始放置皇后。
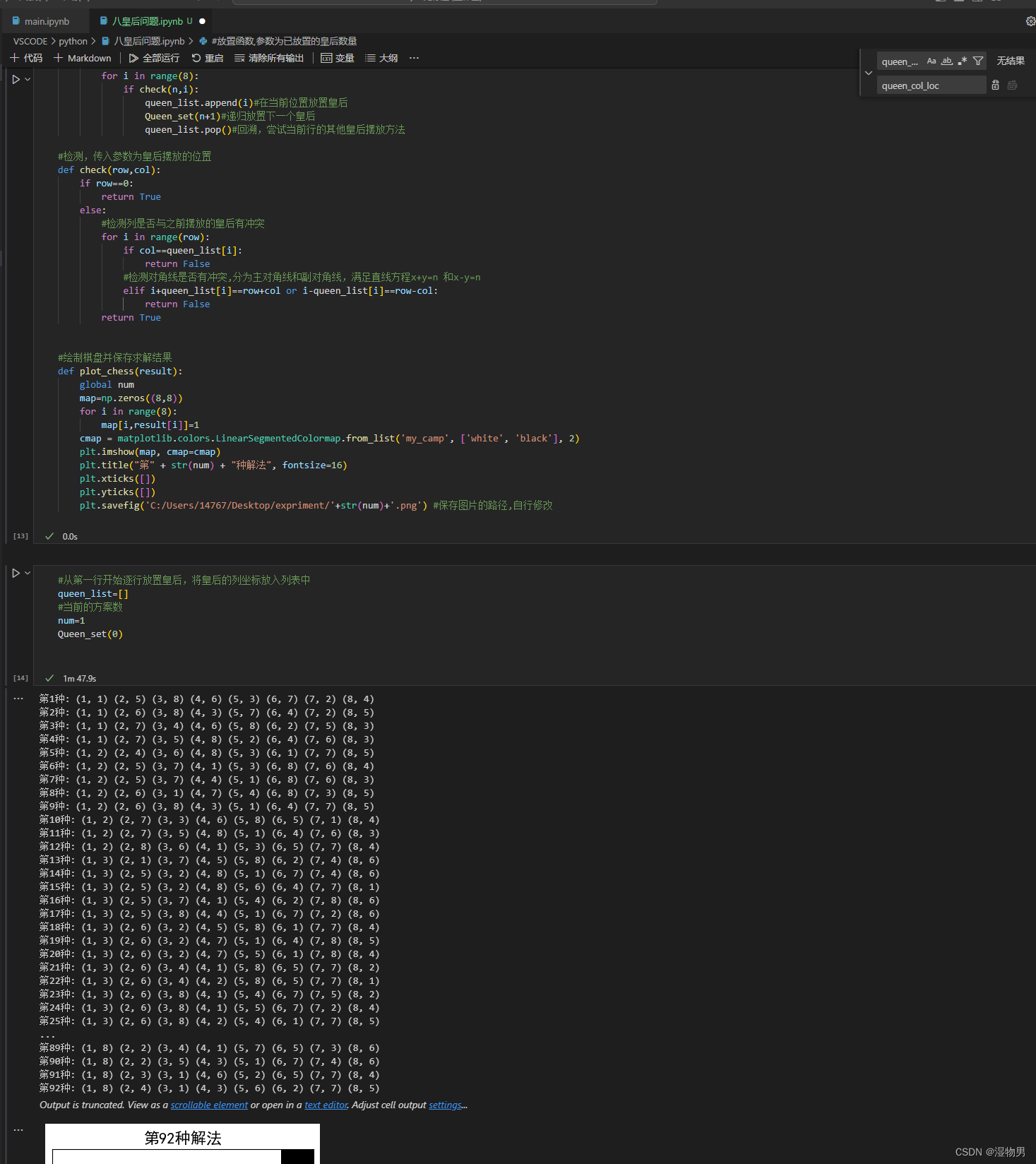
图3-1 回溯法解决八皇后问题运行结果
| 目录: 代码段一:导包 代码段二:函数定义 代码段三:调用运行 |
| 导包 |
| import numpy as np import matplotlib import matplotlib.pyplot as plt #设定中文字符集,解决绘图时中文乱码问题 matplotlib.rcParams['font.sans-serif'] = ['SimHei'] |
| 函数定义 |
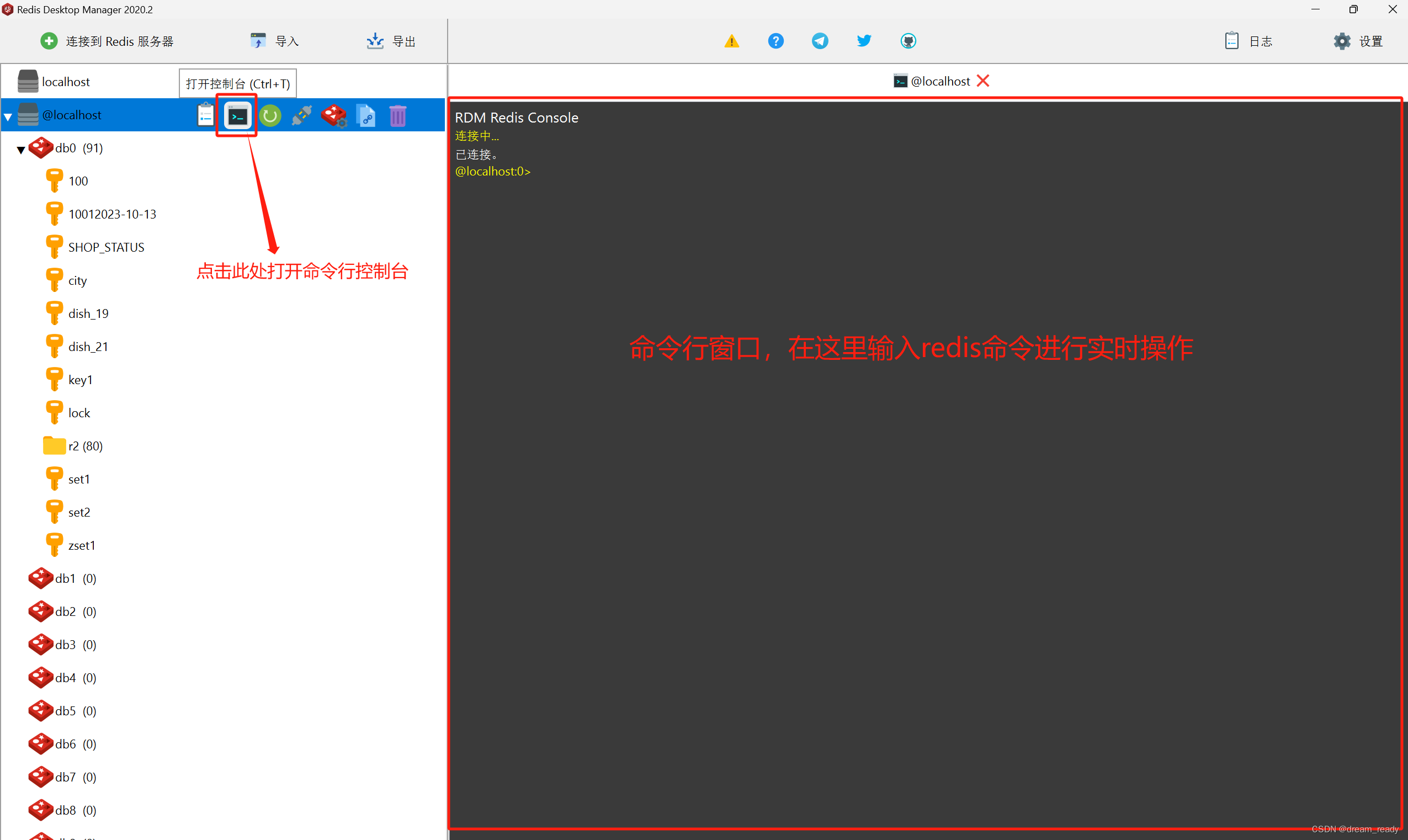
| #放置函数,参数为已放置的皇后数量 def Queen_set(n): global num global queen_list queen_col_loc=[i+1 for i in queen_list] #方案可行 if n==8: print("第"+str(num)+"种:",(1,queen_col_loc[0]),(2,queen_col_loc[1]),(3,queen_col_loc[2]),(4,queen_col_loc[3]) ,(5,queen_col_loc[4]),(6,queen_col_loc[5]),(7,queen_col_loc[6]),(8,queen_col_loc[7])) #绘制当前的皇后摆放方案 plot_chess(queen_list) num+=1 return else: #检查当前行哪一个位置可以放置 for i in range(8): if check(n,i): queen_list.append(i)#在当前位置放置皇后 Queen_set(n+1)#递归放置下一个皇后 queen_list.pop()#回溯,尝试当前行的其他皇后摆放方法 #检测,传入参数为皇后摆放的位置 def check(row,col): if row==0: return True else: #检测列是否与之前摆放的皇后有冲突 for i in range(row): if col==queen_list[i]: return False #检测对角线是否有冲突,分为主对角线和副对角线,满足直线方程x+y=n 和x-y=n elif i+queen_list[i]==row+col or i-queen_list[i]==row-col: return False return True
#绘制棋盘并保存求解结果 def plot_chess(result): global num map=np.zeros((8,8)) for i in range(8): map[i,result[i]]=1 cmap = matplotlib.colors.LinearSegmentedColormap.from_list('my_camp', ['white', 'black'], 2) plt.imshow(map, cmap=cmap) plt.title("第" + str(num) + "种解法", fontsize=16) plt.xticks([]) plt.yticks([]) plt.savefig('C:/Users/14767/Desktop/expriment/'+str(num)+'.png') #保存图片的路径,自行修改 |
| 调用运行 |
| #从第一行开始逐行放置皇后,将皇后的列坐标放入列表中 queen_list=[] #当前的方案数 num=1 Queen_set(0) |

图3-2 八皇后问题解法可视化部分结果