2023 香山杯 --- Crypto wp-编程知识

2023 香山杯 --- Crypto wp

文章目录

- - 题目
  - 解题思路
  - 解题代码

题目

import os
import gmpy2
from Crypto.Util.number import *
import random
from secrets import flag
def pad(s,l):return s + os.urandom(l - len(s))
def gen():g = getPrime(8)while True:p = g * random.getrandbits(138) + 1if isPrime(p):breakwhile True:q = g * random.getrandbits(138) + 1if isPrime(q):breakN = p ** 5 * qphi = p ** 4 * (p - 1) * (q - 1)d = random.getrandbits(256)e = inverse(d, phi)E = e * ghint = gmpy2.gcd(E, phi)return N, E, hintflag = pad(flag,64)
m = bytes_to_long(flag)
n,e,hint = gen()
c = pow(m,e,n)
print(f'hint = {hint}')
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
# hint = 251
# n = 108960799213330048807537253155955524262938083957673388027650083719597357215238547761557943499634403020900601643719960988288543702833581456488410418793239589934165142850195998163833962875355916819854378922306890883033496525502067124670576471251882548376530637034077
# e = 3359917755894163258174451768521610910491402727660720673898848239095553816126131162471035843306464197912997253011899806560624938869918893182751614520610693643690087988363775343761651198776860913310798127832036941524620284804884136983215497742441302140070096928109039
# c = 72201537621260682675988549650349973570539366370497258107694937619698999052787116039080427209958662949131892284799148484018421298241124372816425123784602508705232247879799611203283114123802597553853842227351228626180079209388772101105198454904371772564490263034162

解题思路

根据题目代码，得到如下信息
$p = g * a + 1, q = g * b + 1$
$E = e g$
$phi = p^4(p-1)*(q-1)=p^4g^2ab$
又因为 $g c d (E, p hi) = hin t = 251$
由此得到， $g = 251$
进而可以得到 $\frac{E}{g}$
根据论文
New attacks on RSA with Moduli $N = p ^rq$
部分
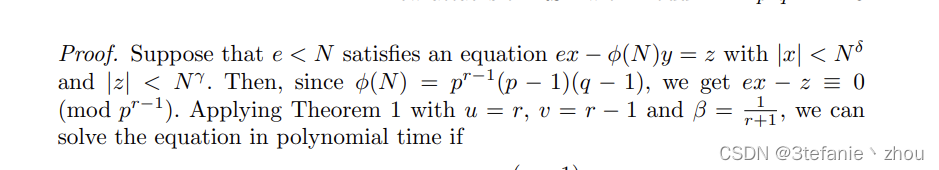
在这里插入图片描述
我们可以将 $\equiv 1 \space mod \space p^4(p-1)*(q-1)$
转化为
$\equiv 1 \space mod \space p^4$
由此可以构建一个多项式环
$\space mod \space p^4$
其中d为256bit

#sage 
n = 108960799213330048807537253155955524262938083957673388027650083719597357215238547761557943499634403020900601643719960988288543702833581456488410418793239589934165142850195998163833962875355916819854378922306890883033496525502067124670576471251882548376530637034077
e = 3359917755894163258174451768521610910491402727660720673898848239095553816126131162471035843306464197912997253011899806560624938869918893182751614520610693643690087988363775343761651198776860913310798127832036941524620284804884136983215497742441302140070096928109039
c = 72201537621260682675988549650349973570539366370497258107694937619698999052787116039080427209958662949131892284799148484018421298241124372816425123784602508705232247879799611203283114123802597553853842227351228626180079209388772101105198454904371772564490263034162
R.<x> = PolynomialRing(Zmod(n))
f = (e//251)*x - 1
root = f.monic().small_roots(X = 2^256,beta=0.5)
print(root)

解出d为

d = 39217838246811431279243531729119914044224429322696785472959081158748864949269

又有
$\equiv0 \space mod \space p^4$
进而可以求出 $\sqrt[4]{gcd(ed-1,n)}$
由于 $g c d (e, p hi) = 251$
所以转为有限域下开根
flag经过pad之后长度为512bit，而p和q只有146bit，组合p和q再crt是不够计算出flag的。
因此，我们将在模n的RSA转为在模 $p^5$ 下的RSA
$n = p^5$
$phi = p^4(p-1)$
$m^{251} = pow(c,d,p^5)$
一开始想用常规有限域下开根去解方程

#sage
R.<x> = Zmod(p^5)[]
f = x^251-m
f = f.monic()
results1 = f.roots()

不知道啥情况，一直没有解

在这里插入图片描述
但是捏
山重水复疑无路，柳暗花明又一春
找到了一个新的用法
我们可以利用nth_root()求出在模 $p^5$ 下的 $m$ 所有可能的根
再遍历所有的根，直到找到flag为止

解题代码

#sage 
from Crypto.Util.number import *
import gmpy2n = 108960799213330048807537253155955524262938083957673388027650083719597357215238547761557943499634403020900601643719960988288543702833581456488410418793239589934165142850195998163833962875355916819854378922306890883033496525502067124670576471251882548376530637034077
e = 3359917755894163258174451768521610910491402727660720673898848239095553816126131162471035843306464197912997253011899806560624938869918893182751614520610693643690087988363775343761651198776860913310798127832036941524620284804884136983215497742441302140070096928109039
c = 72201537621260682675988549650349973570539366370497258107694937619698999052787116039080427209958662949131892284799148484018421298241124372816425123784602508705232247879799611203283114123802597553853842227351228626180079209388772101105198454904371772564490263034162#get d  and p
R.<x> = PolynomialRing(Zmod(n))
f = (e//251)*x - 1
root = f.monic().small_roots(X = 2^256,beta=0.5)
d = int(root[0])
p_4 = GCD(e//251*d-1,n)
p = gmpy2.iroot(p_4,4)[0]#find all possible roots to ergodic flag
phi = p^4*(p-1)
d1 = inverse_mod(e//251,phi)
m = pow(c,d,p^5)
result = Zmod(p^5)(m).nth_root(251,all=True)
for i in result:flag = long_to_bytes(int(i))if b'flag{' in flag:print(flag)break