编码与调制

        消息是以二进制的形式存放在数据当中的，这种数据的表现形式是信号，而信源发出的原始信号就叫做基带信号，基带信号又可以分为数字基带信号和模拟基带信号。
        信号需要在信道中进行传输，信道分为模拟信道和数字信道，在不改变信号性质的前提，仅对数字基带信号进行波形变换，称为编码 。编码后的信号认为数字信号。把数字信号的频带搬移到较高频段后称为调制，调制后生成的信号为模拟信号。
        码元：在使用时间域的波形表示数字信号时，代表不同离散数值的基本波形。
        传输媒体并不等价于信道。

几种常用的编码

比特流： 1 0 0 1 0 1 0 1
不归零编码 ：+ - - + - + - +
以上两种编码会常常出现一个问题：当多个同样的电平连续出现时，计算机如何判断其包含了几个码元
归零编码：+ 0 - 0 - 0 + 0 - 0 + 0
归零编码就不会出现以上问题了。
**曼彻斯特编码：**每一个码元中间时刻电平的跳变，正跳变表示0，负跳变表示1。

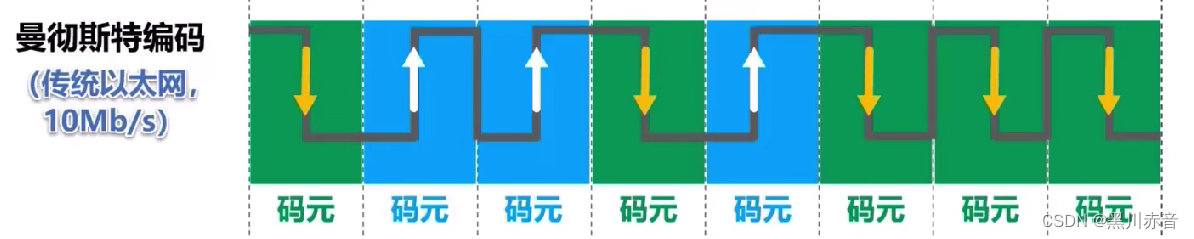
差分曼彻斯特编码：

差分曼彻斯特编码的跳变代表时钟，上一个码元结束和下一个码元开始的电平是否产生变换来表示编码，发送变化为0，不发生变化为1。

基本调制方法

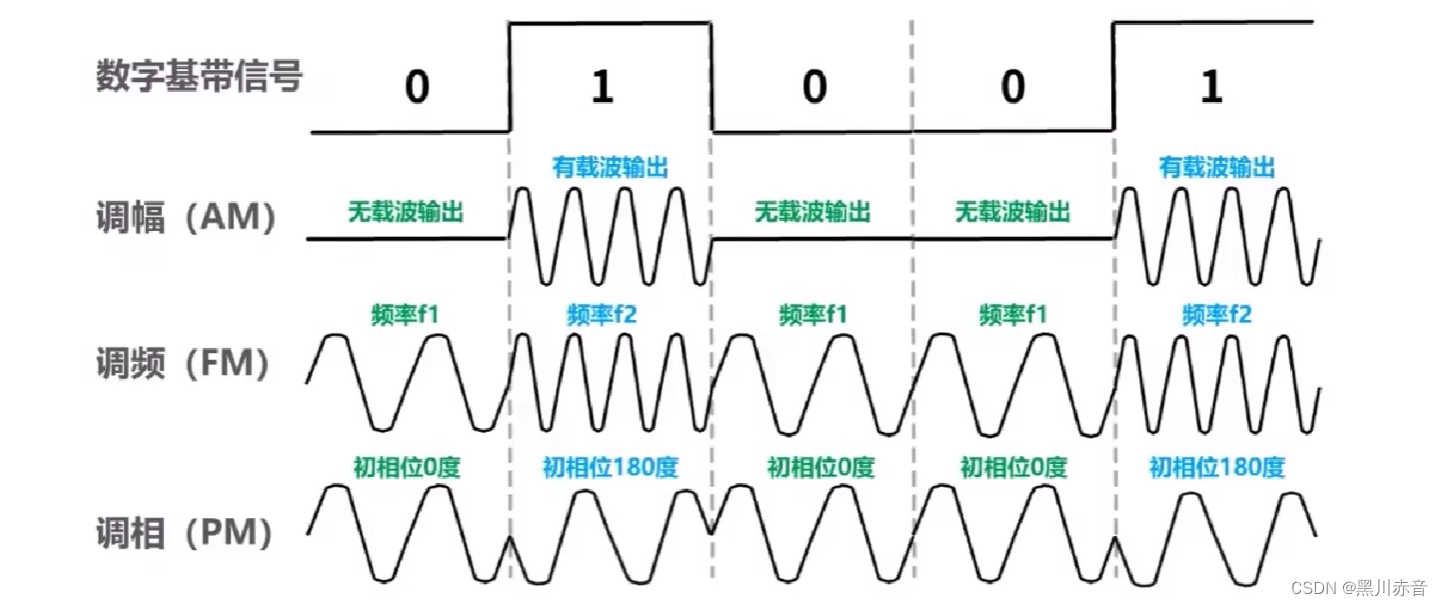
显然，使用基本调制方法，1个码元只能包含1个比特信息，那么如何使一个码元包含多个比特信息？
        采用混合调制：
        相位和振幅调制：（正交振幅调制——QAM）
QAM-16：
        有12种相位，每种相位有1或2种振幅可选
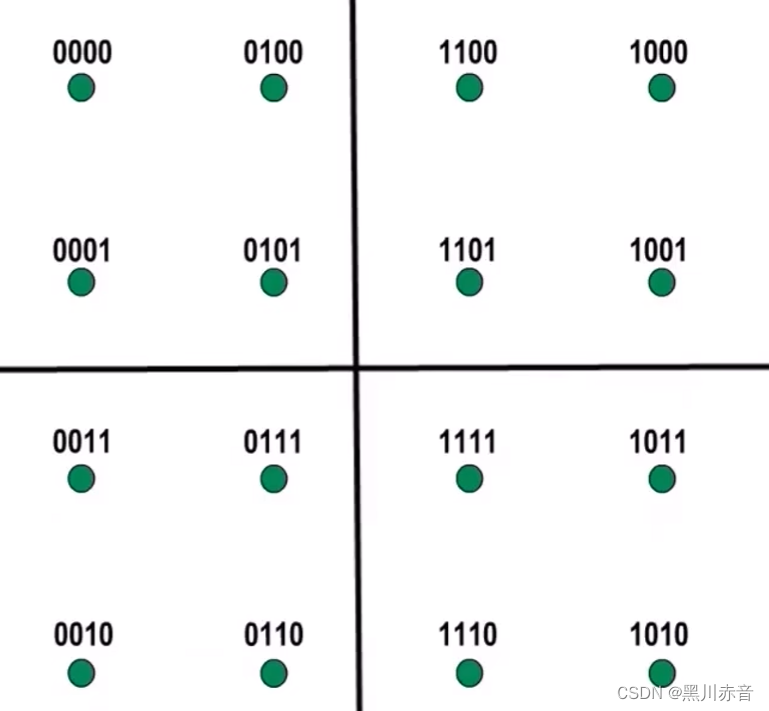
        星座图如下：

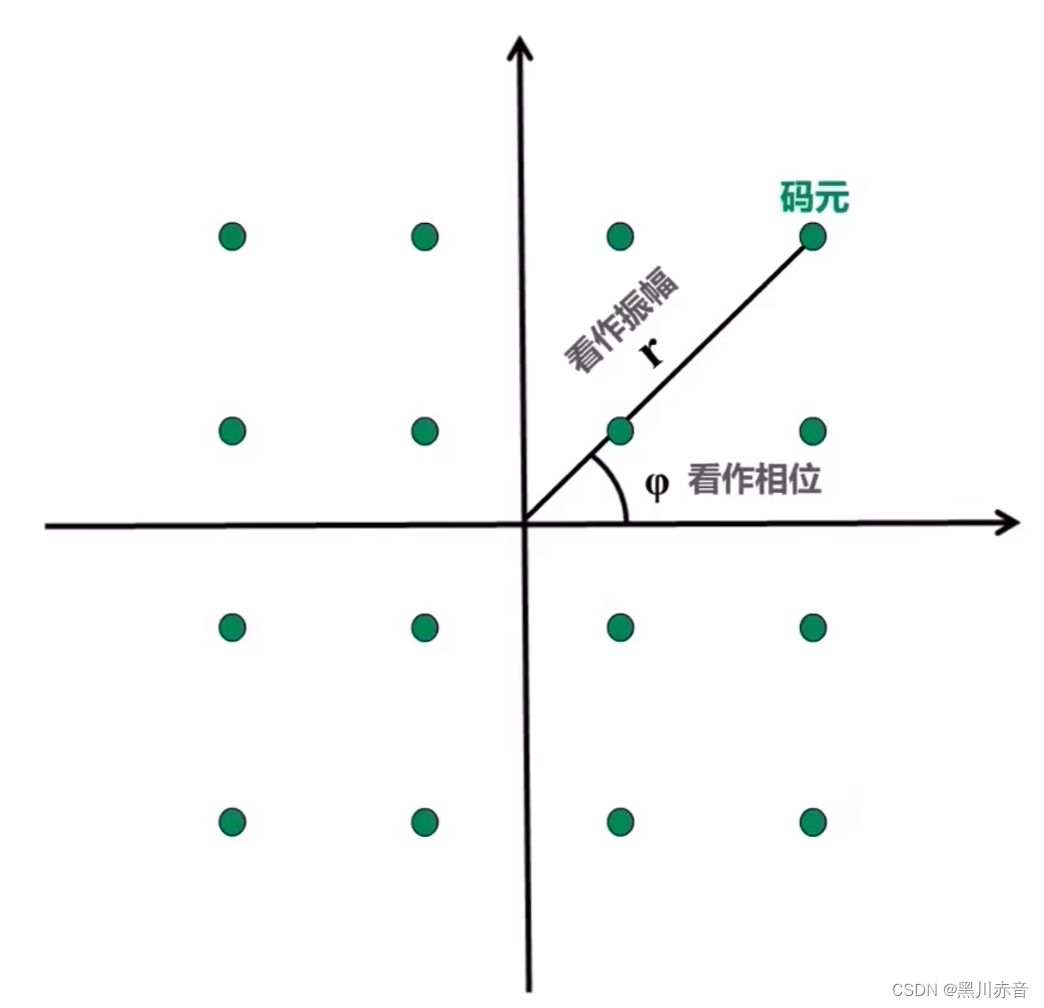
        上图中，每一个点可以代表一个码元，共有16个码元，那么这16个码元正好可以表示0000，0001，0010，…，1111 这些，那么他们可以随便定义吗，如下：

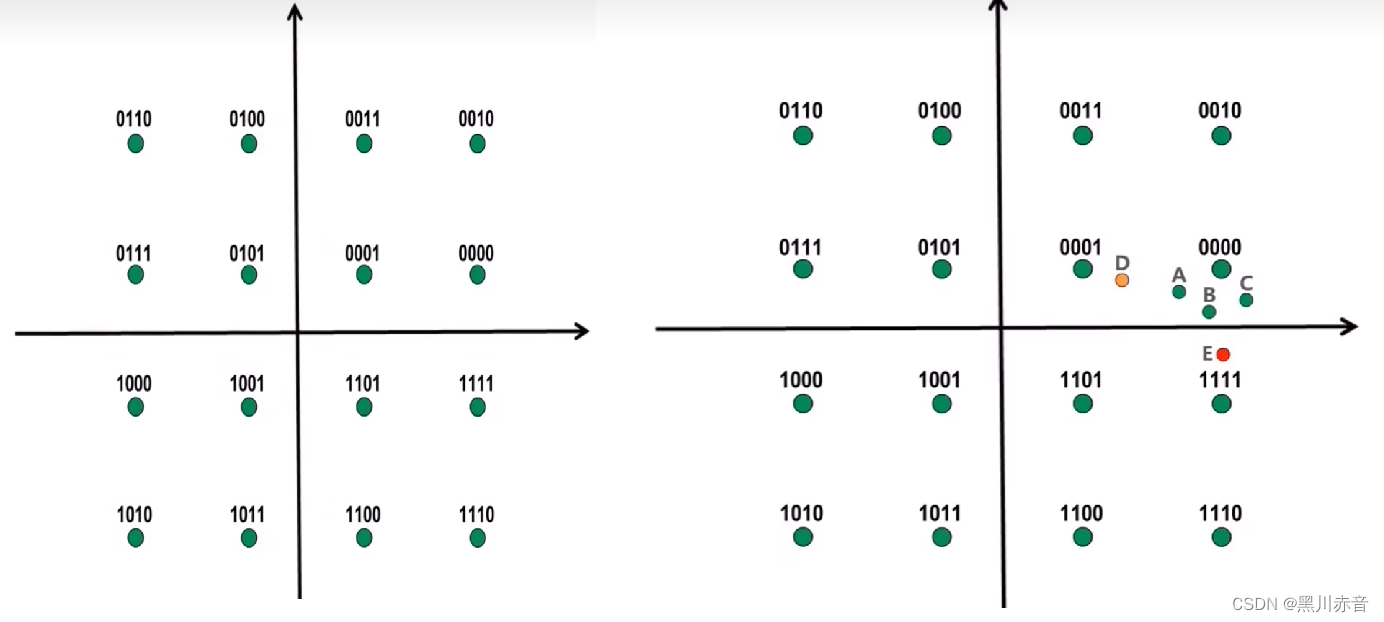
        上面右图0000出现了失真(A,B,C,D,E)，那么会把E看出1111，此时出现了较大错误，因此我们用格雷码来排列，如下：