👦个人主页:Weraphael
✍🏻作者简介:目前正在回炉重造C语言(2023暑假)
✈️专栏:【C语言航路】
🐋 希望大家多多支持,咱一起进步!😁
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注😍
目录
- 一、一维数组
- 1.1 数组的创建和初始化
- 1.2 一维数组的使用
- 1.3 一维数组在内存中的存储(重点)
- 二、二维数组
- 2.1 二维数组的创建和初始化
- 2.2 二维数组的使用
- 2.3 二维数组在内存中的存储
- 三、数组越界
- 四、数组名
- 4.1 验证数组名是首元素地址
- 4.2 数组名不是首元素地址的两个例外
一、一维数组
数组是一组 相同类型元素的集合。
1.1 数组的创建和初始化
- 数组的创建:
type_t arr_name [const_n];//type_t --- 数组的元素类型
//arr_name --- 数组名
//const_n --- 是一个常量表达式(不能使用变量),用来指定数组元素个数
// 但在C99规定:const_n可以使用变量,但是不能初始化!
- 数组的初始化:数组的初始化是指在创建数组的同时给数组的内容一些合理初始值。
【例如】
int arr1[10] = { 1,2,3,4,5,6 };
int arr2[] = { 1,2,3,4,5,6 };
int arr3[5] = { 1,2,3,4,5 };
int arr4[3] = { 'a','b','c' };
int arr5[] = { 'a','b','c' };
int arr6[] = "abcdef";
- 对于第一种未满
10个元素的叫 不完全初始化(剩余的元素默认初始化为0)[]内也可以不指定元素个数,这时编译器会根据初始化的内容来确定数组的元素个数。- 对于字符数组,需要用单引号,它的不完全初始化是
'\0'(ASCII码值是0);对于字符串数组,则用双引号,而它的不完全初始化(剩余的元素默认初始化也是'\0')- 若有一个全局变量的整型数组且未被初始化,它的元素默认为0。
看看以下程序:
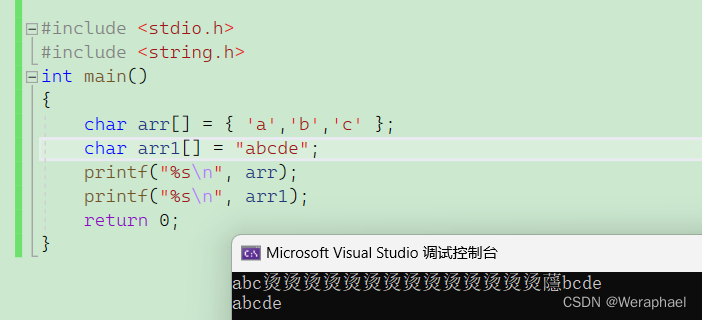
- 若要打印字符串数组,就会打印出
'\0'往前的内容,因为字符串的结束标志是'\0'。- 但要打印字符数组,除了打印出初始化的内容,因为找不到结束标志
'\0',则后面打印出随机值。
1.2 一维数组的使用
[]:下标引用操作符。它是用来数组访问的操作符。- 数组元素是通过下标访问的,且下标从
0开始的
【样例】
打印1~10
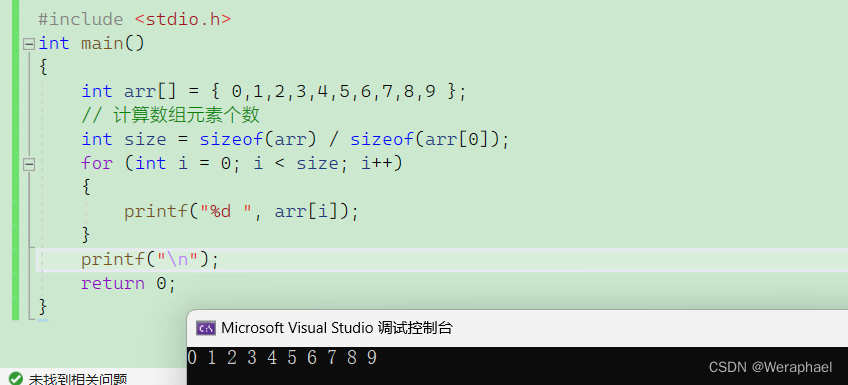
还可以倒序输出
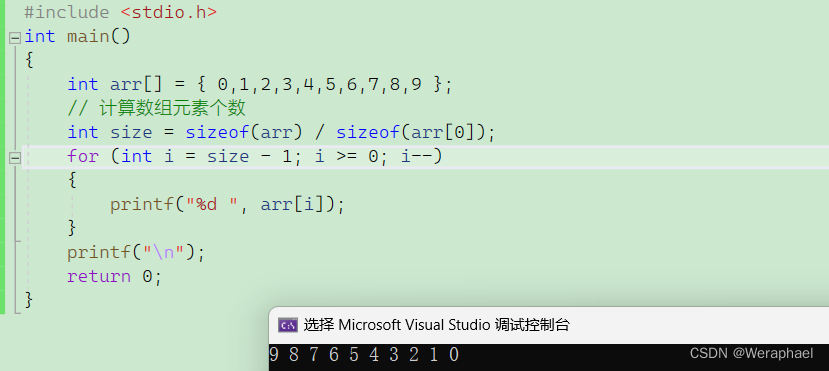
或者还可以跳着打印
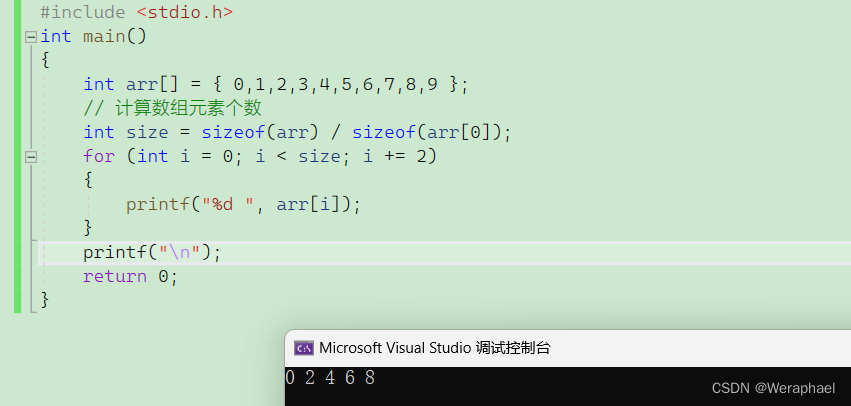
1.3 一维数组在内存中的存储(重点)
怎么知道一维数组在内存中的存储呢?可以把地址打印出来观察
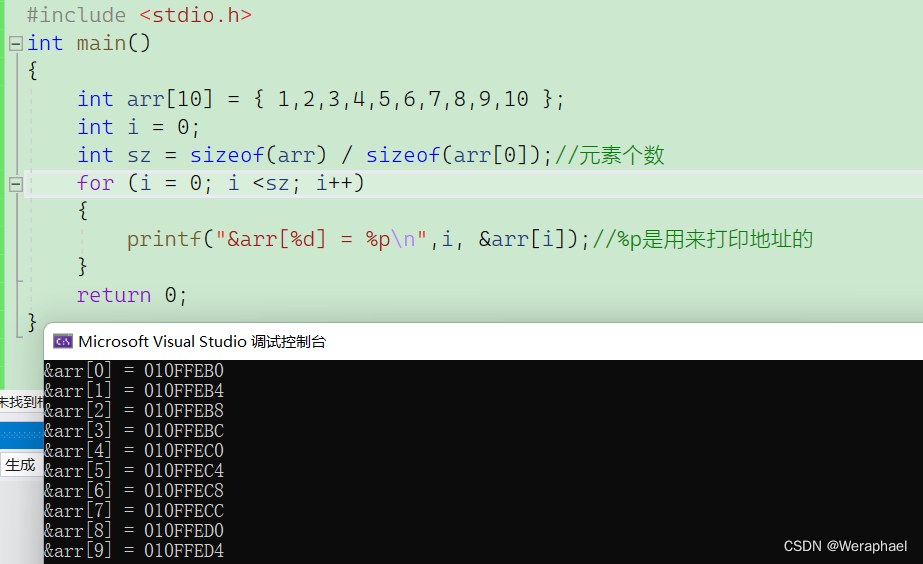
通过观察发现:由于数组的元素都是
int类型,因此地址之间差4个字节,并且都是连续的,所以可以得出以下结论:
- 一维数组在内存中是连续存放的。
- 随着数组下标的增长,地址是由低到高变化的。
接下来通过图来加以分析:
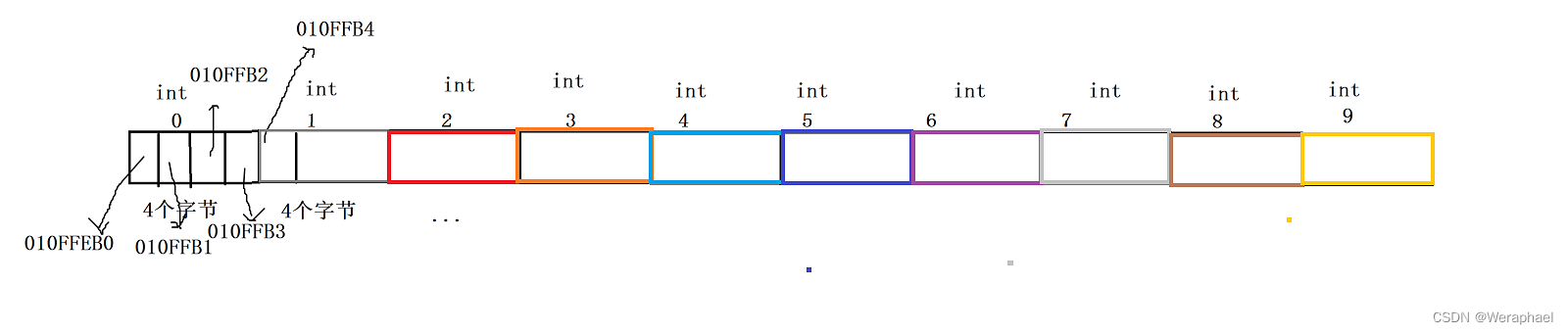
所以,通过以上两个结论,只要得到了数组首元素的地址,就能顺藤摸瓜找出所有数组的地址。
举个例子:
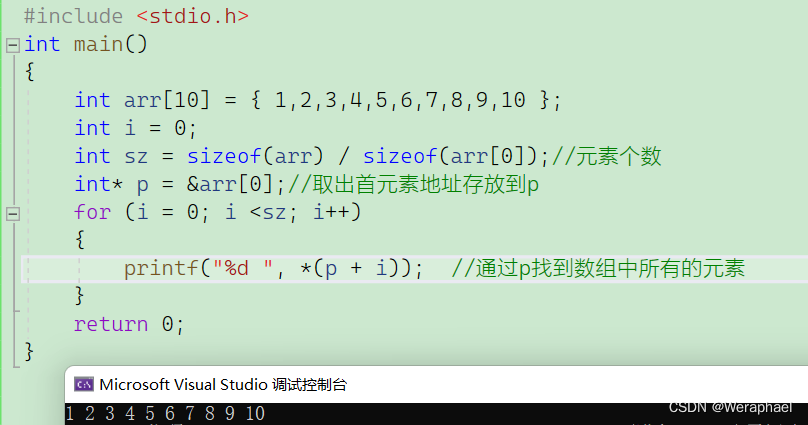
解释一下
*(p+i),举个例子,当i=0时,p+i还是p,此时指向首元素的地址,通过解引用,找到了数组元素1
以往我们打印数组的地址都是用&arr[i]来访问,所以为了确保真实性,可以验证指针p+i的地址与&arr[i]的地址:

显然是一模一样的!!
二、二维数组
若想知道二维数组的元素个数,只需将行与列相乘即可。
2.1 二维数组的创建和初始化
- 二维数组的创建
int arr[3][4] //表示3行4列
char arr[3][5] //表示3行5列
double arr[2][4] //表示2行3列
- 二维数组的初始化
- 完全初始化

- 不完全初始化

不完全初始化的二维数组后面依然补0
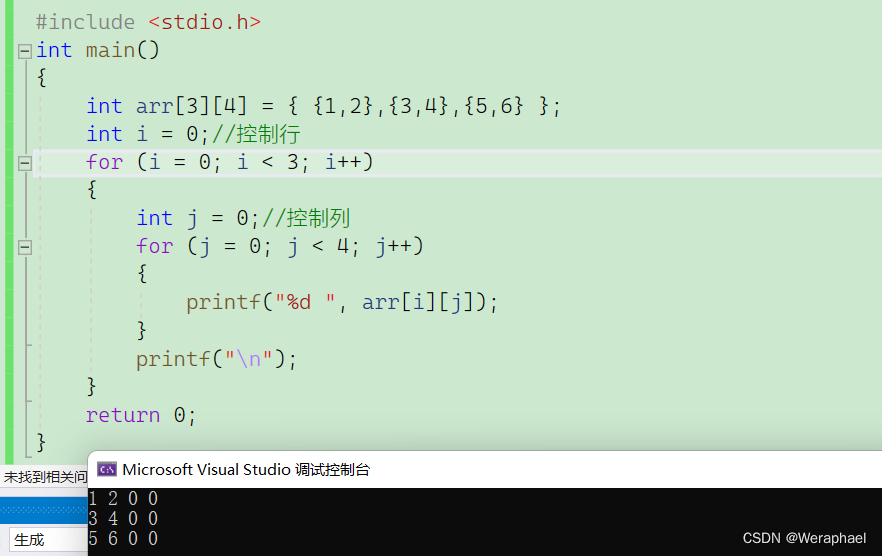
- 假如我想在一个整型数组3行4列中,第一行放1,2,第二行放3,4,第三行放5,6,这就要牵扯另一种初始化方式:可以将行当作一维数组

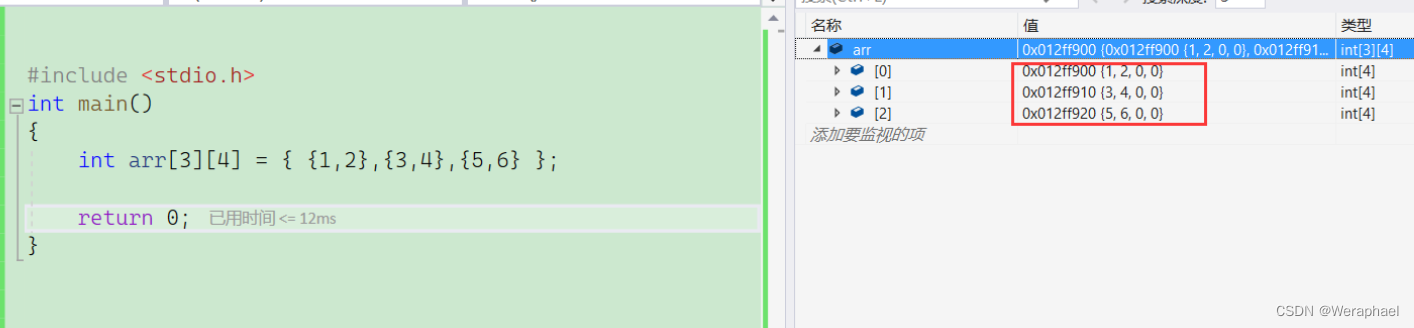
- 注意:二维数组如果有初始化,行可以省略,列不能省略!!!
int arr[][4] = {0};
2.2 二维数组的使用
二维数组的使用也是通过 下标 的方式来访问
下面是一个三行四列的整型数组
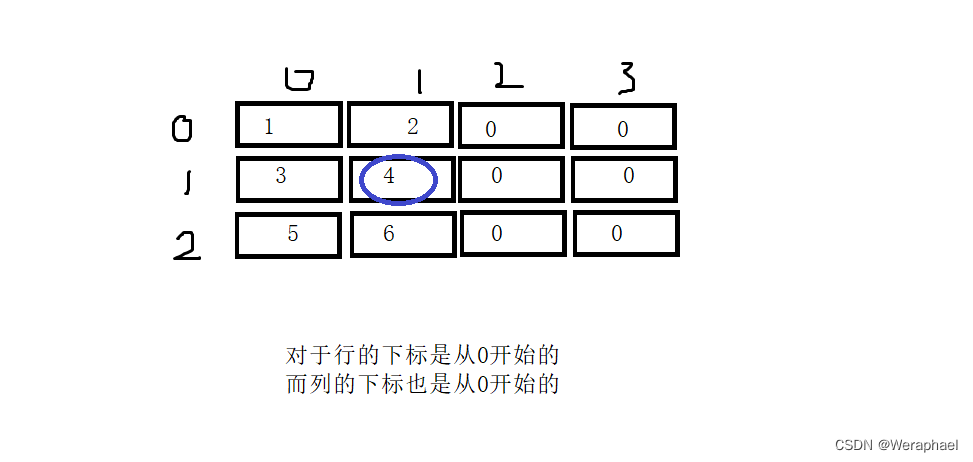
假设我要打印4,而4对应则是arr[1][1]
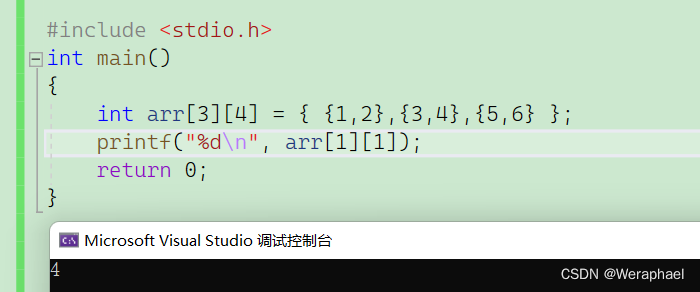
或者还能打印这整个数组
2.3 二维数组在内存中的存储
怎么知道二维数组在内存中的存储呢?可以同样可以把地址打印出来观察
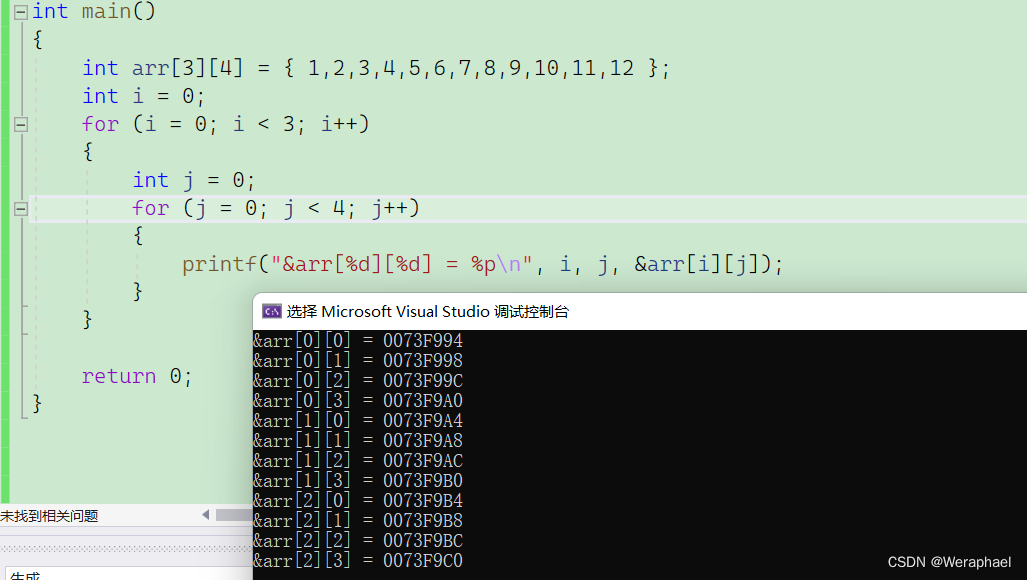
观察发现:地址之间还是差4个字节,所以得出结论:二维数组和一维数组一样都是连续存储的
所以二维数组的排列方式可以变成如下图所示:
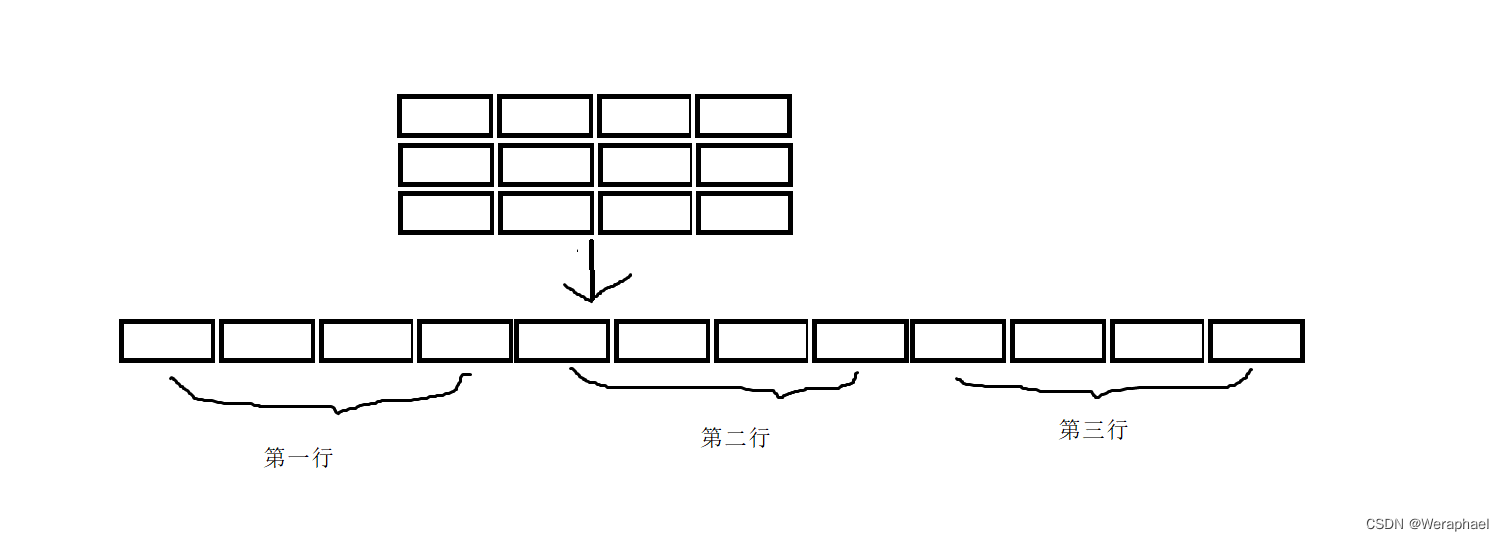
既然二维数组是连续存放的,且二维数组的排列方式也像一维数组。因此,我们可以把二维数组看成12个元素的一维数组。所以,只要得到了数组首元素的地址,就能顺藤摸瓜找出所有数组的地址。
例如:
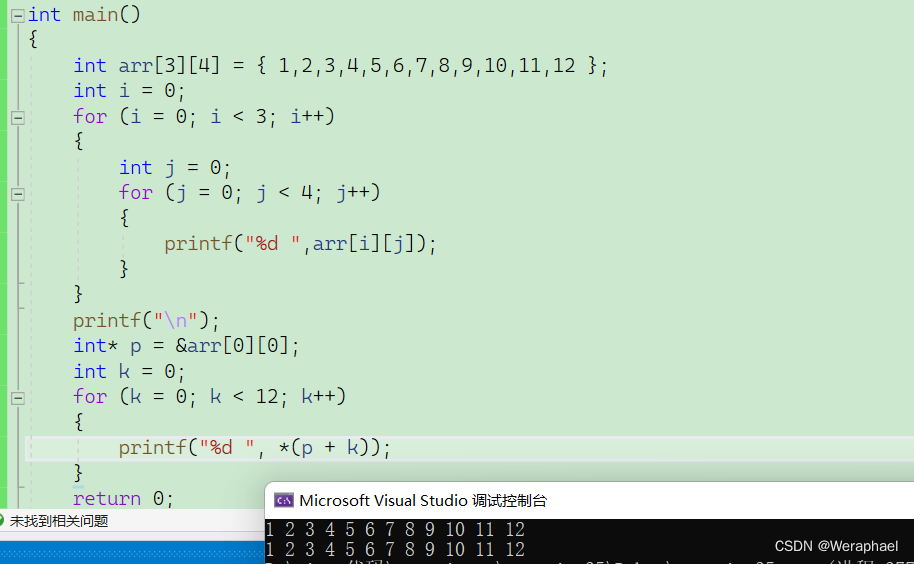
- 补充
刚刚讲过可以将行当作一维数组,而在访问一维数组时,我们都会通过一个变量来访问下标,如下图,我们可以将三行分别看作下标为0 1 2 3 4的一维数组,对于第一、二、三行来说,行都是不变的,变的只有列,所以可以这样理解,把arr[0]、arr[1]、arr[2]分别当作第一行、第二行和第三行的数组名。
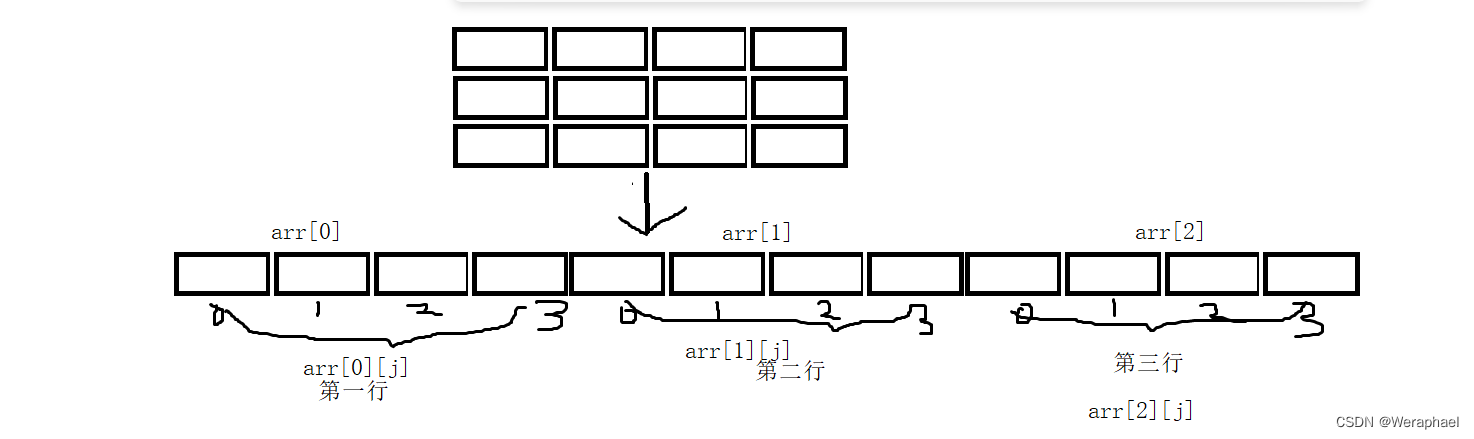
所以也能这样打印数组:
#include<stdio.h>
int main()
{int arr[3][4] = { 1,2,3,4,5,6,7,8,9,10,11,12 };//整个大小(48)/第一行的大小(16)= 3for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){//第一行的大小(16)/第一行第一列的大小(4)=4for (int j = 0; j < sizeof(arr[0]) / sizeof(arr[0][0]); j++){printf("%d ", arr[i][j]);}}return 0;
}
三、数组越界
- 首先数组的下标是有范围限制的。
- 数组的下规定是从
0开始的,如果数组有n个元素,最后一个元素的下标就是n-1。所以数组的下标如果小于0,或者大于n-1,就是数组越界访问了,超出了数组合法空间的访问。- C 语言本身是不做数组下标的越界检查,编译器也不一定报错,但是编译器不报错,并不意味着程序就是正确的,所以程序员写代码时,最好自己做越界的检查
比如下面的代码:
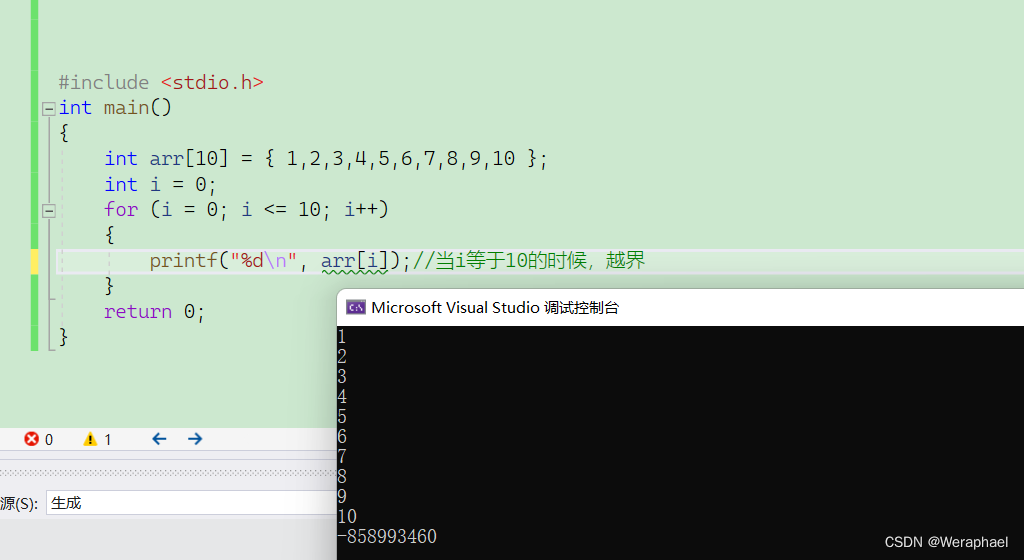
注意: 二维数组的行和列也可能存在越界。
四、数组名
4.1 验证数组名是首元素地址
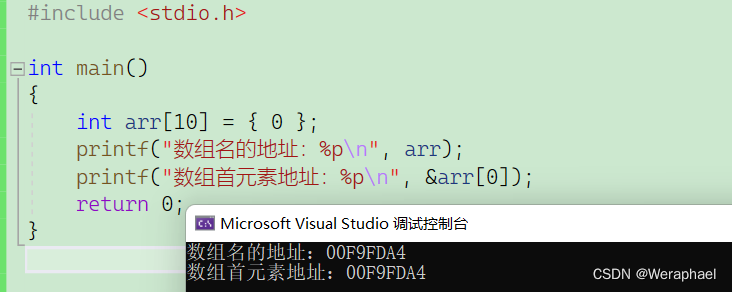
通过对比其地址,可见数组名就是首元素地址。
4.2 数组名不是首元素地址的两个例外
sizeof(数组名)
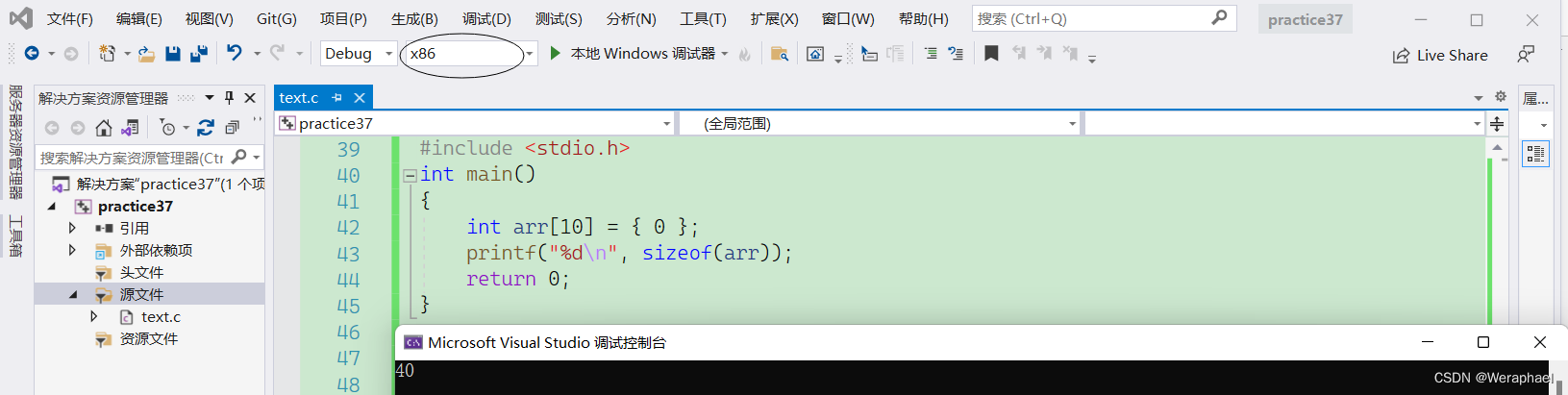
刚刚验证了数组是首元素地址,一个地址的大小无非是8字节(x64环境)或者4字节(x86环境),而上面的代码却打印了40个字节,这是什么原因呢?这就是其中一个例外:当
sizeof内部单独放一个数组名时,这里的数组名表示整个数组,计算是整个数组的大小,单位是字节。
&数组名

这里的数组名也表示整个数组,&数组名取出的是整个数组的地址。在这里,你们肯定发现了,&arr打印的不也是首元素的地址吗?这里我画图为大家分析:
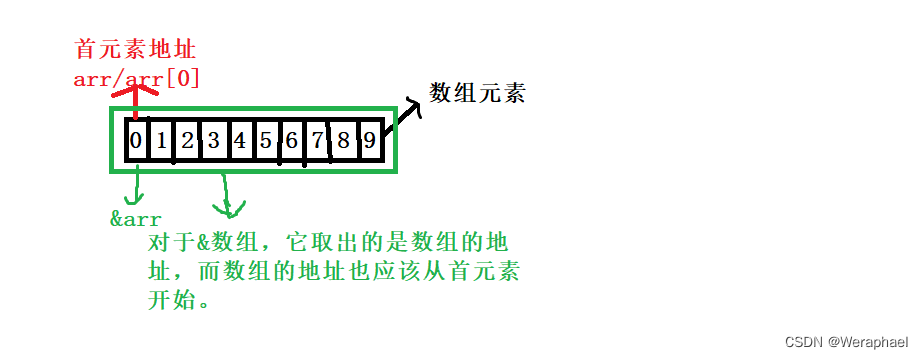
虽然它们的地址是一样的,但是意义不一样,举个例子:
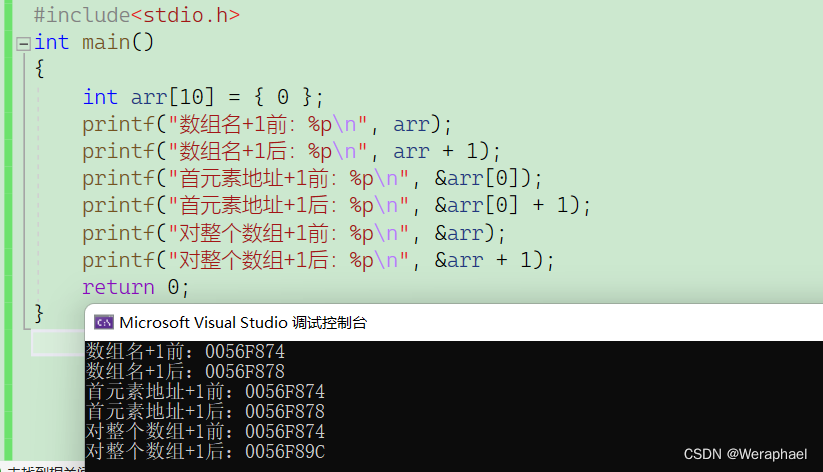
数组名本质上和首元素地址一样,如果是数组名+1或者是首元素地址+1,他们都是跳过对应类型的大小;但由于&数组名取出的是整个数组的地址,因此&数组名+1,跳过的是整个数组的大小。