【动态规划】392. 判断子序列、115. 不同的子序列-编程知识

【动态规划】392. 判断子序列、115. 不同的子序列

提示：努力生活，开心、快乐的一天

文章目录

392. 判断子序列
- 💡解题思路
- 🤔遇到的问题
- 💻代码实现
- 🎯题目总结
115. 不同的子序列
- 💡解题思路
- 🤔遇到的问题
- 💻代码实现
- 🎯题目总结
🎈今日心得

392. 判断子序列

题目链接：392. 判断子序列

💡解题思路

该题与1143.最长公共子序列基本一致，不同点主要有2个
- 本题如果删元素一定是字符串t，而 1143.最长公共子序列是两个字符串都可以删元素。这就导致在确定递推公式的时候，针对(s[i - 1] != t[j - 1])情况，两道题的公式不一样
- 最终返回结果，该题需要返回的是dp[s.length][t.length]（最长公公子序列的长度）与s.length是否相等
动规五部曲

确定dp数组以及下标的含义：dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]
确定递推公式：主要就是两大情况： s[i - 1] 与 [j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同
如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
dp数组如何初始化：dp[i][0] = 0；dp[0][j] = 0
确定遍历顺序：从递推公式，可以看出，有三个方向可以推出dp[i][j]
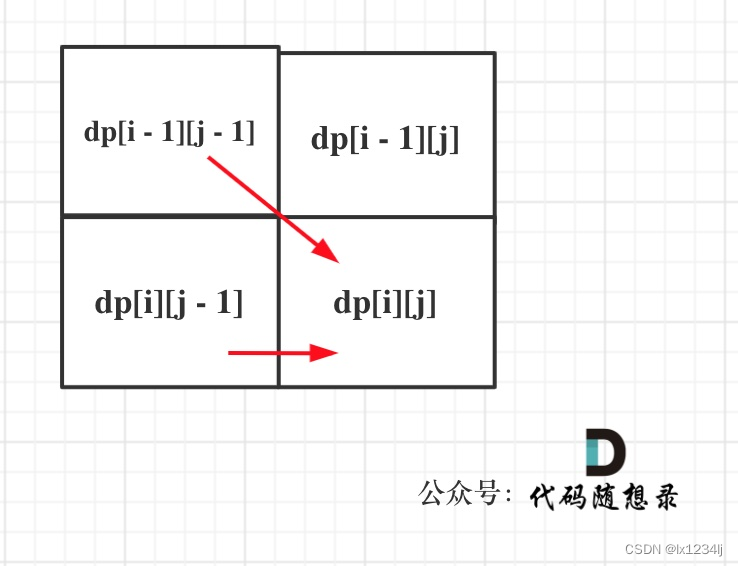
举例推导dp数组：按照递推公式推导一下做推导，如果发现结果不对，就把dp数组打印出来

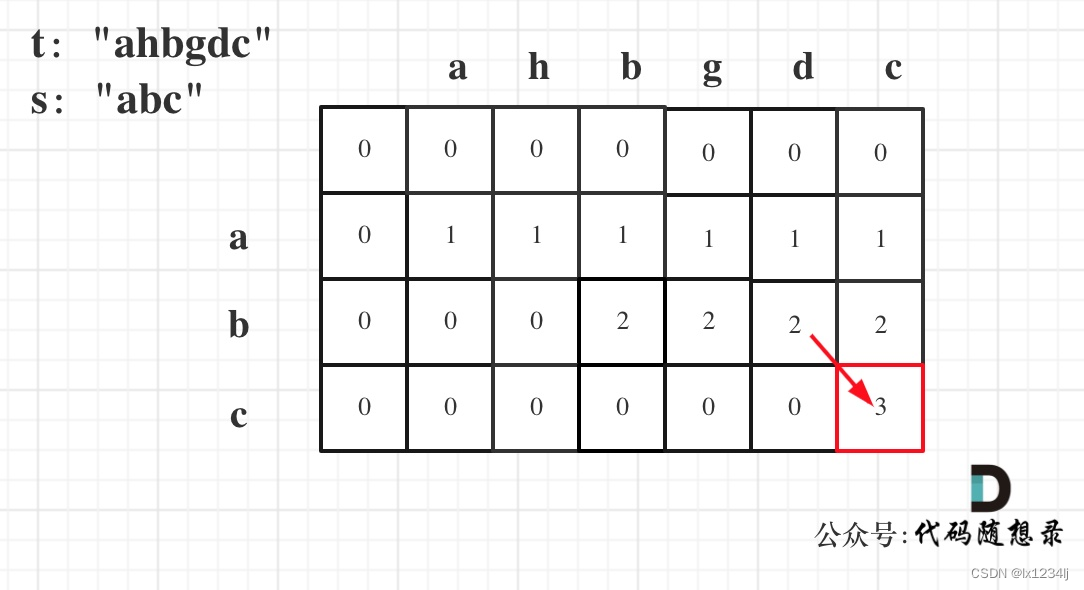
🤔遇到的问题

最后的返回结果，是dp[s.length][t.length]（最长公公子序列的长度）与s.length是否相等

💻代码实现

动态规划

var isSubsequence = function (s, t) {let dp = new Array(s.length + 1).fill(0).map(x => new Array(t.length + 1).fill(0))for (let i = 1; i <= s.length; i++) {for (let j = 1; j <= t.length; j++) {if (s[i - 1] === t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1} else {dp[i][j] = dp[i][j - 1]}}}return dp[s.length][t.length] === s.length ? true : false
};

🎯题目总结

dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度，所以如果dp[s.size()][t.size()] 与字符串s的长度相同说明：s与t的最长相同子序列就是s，那么s 就是 t 的子序列。

115. 不同的子序列

题目链接：115. 不同的子序列

💡解题思路

动规五部曲

确定dp数组以及下标的含义：dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]
确定递推公式：主要就是两大情况： s[i - 1] 与 [j - 1]相同，s[i - 1] 与 t[j - 1]不相同
如果s[i - 1] 与 t[j - 1]相同，dp[i][j]可以有两部分组成：
一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母，所以只需要 dp[i-1][j-1]；一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
如果s[i - 1] 与 t[j - 1]不相同，dp[i][j]只有一部分组成，不用s[i - 1]来匹配（就是模拟在s中删除这个元素），即：dp[i - 1][j]
dp数组如何初始化：
dp[i][0] = 1；dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数，以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1
dp[0][j] = 0；dp[0][j]表示：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数，那么dp[0][j]一定都是0，s如论如何也变成不了t
特殊位置：dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t
确定遍历顺序：从递推公式，可以看出，有三个方向可以推出dp[i][j]
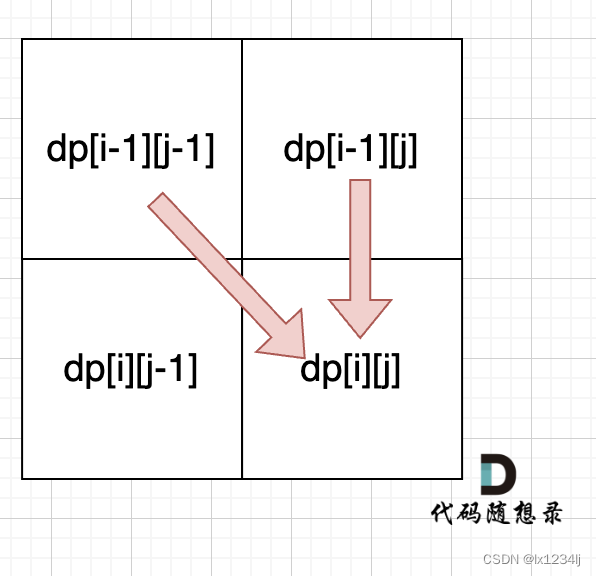
举例推导dp数组：按照递推公式推导一下做推导，如果发现结果不对，就把dp数组打印出来

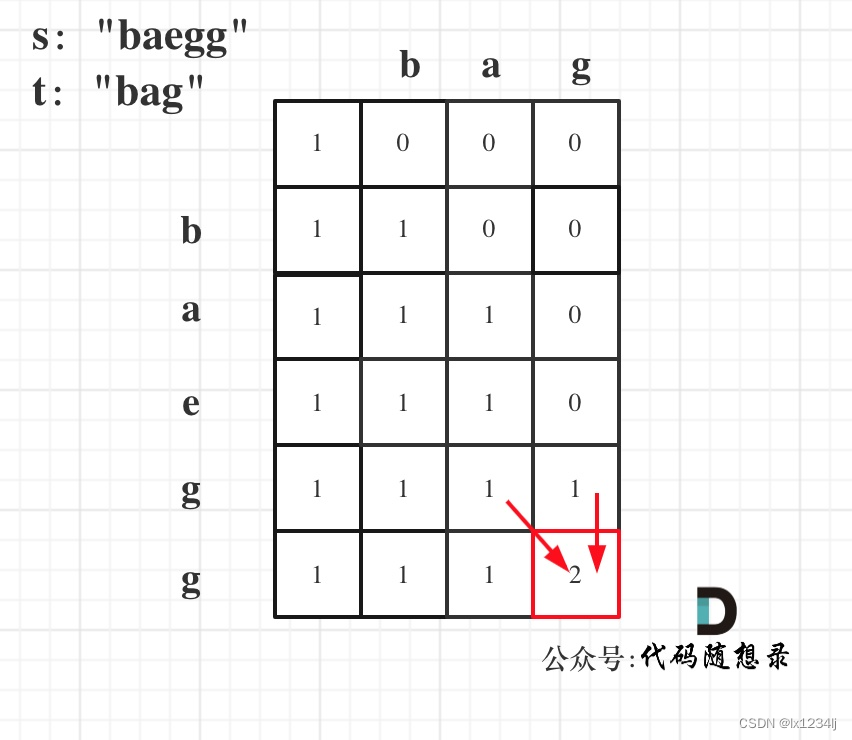
🤔遇到的问题

因为dp[i][j]的含义，所以在遍历s和t的时候，都可以等于s.length或者t.length

💻代码实现

动态规划

var numDistinct = function (s, t) {//s：父//t：子let dp = new Array(s.length + 1).fill(0).map(x => new Array(t.length + 1).fill(0))//t为空字符串时for (let i = 0; i <= s.length; i++) {dp[i][0] = 1}for (let i = 1; i <= s.length; i++) {for (let j = 1; j <= t.length; j++) {if (s[i - 1] === t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]} else {dp[i][j] = dp[i - 1][j]}}}console.log(dp)return dp[s.length][t.length]
};

🎯题目总结

重点需要关注的是：当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母，所以只需要 dp[i-1][j-1]。
一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。