文章目录
- 1 :peach:基本概念:peach:
- 1.1 :apple:什么是HTTPS?:apple:
- 1.2 :apple:什么是加密?:apple:
- 1.3 :apple:常见的加密方式:apple:
- 1.3.1 :lemon:对称加密:lemon:
- 1.3.2 :lemon:⾮对称加密:lemon:
- 1.4 :lemon:数据指纹:lemon:
- 2 :peach:HTTPS的⼯作过程探究:peach:
- 2.1 :apple:只使用对称加密:apple:
- 2.2 :apple:只使用非对称加密:apple:
- 2.3 :apple:双方都使用非对称加密:apple:
- 2.4 :apple:非对称加密 + 对称加密:apple:
- 3 :peach:证书:peach:
- 3.1 :apple:CA认证:apple:
- 3.2 :apple:数据签名:apple:
- 3.3 :apple:非对称加密 + 对称加密 + 证书认证:apple:
- 3.4 :apple:常见问题:apple:
- 3.4.1 :lemon:中间人有没有可能篡改该证书?:lemon:
- 3.4.2 :lemon:中间人有没有可能整个掉包证书?:lemon:
- 3.4.3 :lemon:为什么摘要内容在网络传输的时候⼀定要加密形成签名?:lemon:
- 3.4.4 :lemon:为什么签名不直接加密,⽽是要先hash形成摘要?:lemon:
- 4 :peach:总结:peach:
1 🍑基本概念🍑
1.1 🍎什么是HTTPS?🍎
HTTPS 也是⼀个应⽤层协议. 是在 HTTP 协议的基础上引⼊了⼀个加密层。
HTTP 协议内容都是按照⽂本的⽅式明⽂传输的.,这就导致在传输过程中可能出现⼀些被篡改的情况;HTTPS通过加密的方式可以有效的避免报文的泄漏。
回忆下:http使用的是80端口,而https使用的是443端口
1.2 🍎什么是加密?🍎
- 加密就是把明⽂(要传输的信息)进⾏⼀系列变换, ⽣成密⽂;
- 解密就是把密⽂再进⾏⼀系列变换, 还原成明⽂。
在这个加密和解密的过程中, 往往需要⼀个或者多个中间的数据, 辅助进⾏这个过程, 这样的数据称为密钥。
大家应该在电视上都看见过打仗时通过电报传输军事机密的场景,可以认为这里的加密解密就是对军事机密的加密解密。
1.3 🍎常见的加密方式🍎
1.3.1 🍋对称加密🍋
- 采⽤单钥密码系统的加密⽅法,同⼀个密钥可以同时用作信息的加密和解密,这种加密⽅法称为对加密,也称为单密钥加密,特征:加密和解密所⽤的密钥是相同的。
- 常⻅对称加密算法(了解):DES、3DES、AES、TDEA、Blowfish、RC2等。
- 特点:算法公开、计算量⼩、加密速度快、加密效率⾼。
对称加密其实就是通过同⼀个 “密钥” , 把明⽂加密成密⽂, 并且也能把密⽂解密成明⽂。
1.3.2 🍋⾮对称加密🍋
- 需要两个密钥来进⾏加密和解密,这两个密钥是公开密钥(public key,简称公钥)和私有密钥
(private key,简称私钥)。 - 常⻅⾮对称加密算法(了解):RSA,DSA,ECDSA
- 特点:算法强度复杂、安全性依赖于算法与密钥但是由于其算法复杂,⽽使得加密解密速度没有对
称加密解密的速度快。
⾮对称加密要⽤到两个密钥, ⼀个叫做 “公钥”, ⼀个叫做 “私钥”;公钥和私钥是配对的.,最⼤的缺点就是运算速度⾮常慢,⽐对称加密要慢很多。
- 通过公钥对明⽂加密, 变成密⽂;
- 通过私钥对密⽂解密, 变成明⽂。
也可以反着⽤:
- 通过私钥对明⽂加密, 变成密⽂;
- 通过公钥对密⽂解密, 变成明⽂。
1.4 🍋数据指纹🍋
- 数字指纹(数据摘要),其基本原理是利⽤单向散列函数(Hash函数)对信息进⾏运算,⽣成⼀串固定⻓度的数字摘要。数字指纹并不是⼀种加密机制,但可以⽤来判断数据有没有被窜改。
- 摘要常⻅算法:有MD5、SHA1、SHA256、SHA512等,算法把⽆限的映射成有限,因此可能会有
碰撞。(两个不同的信息,算出的摘要相同,但是概率⾮常低) - 摘要特征:和加密算法的区别是,摘要严格意义不是加密,因为没有解密,只不过从摘要很难反推
原信息,通常⽤来进⾏数据对⽐。
2 🍑HTTPS的⼯作过程探究🍑
既然要保证数据安全, 就需要进⾏ “加密”;⽹络传输中不再直接传输明⽂了, ⽽是加密之后的 “密⽂”;加密的⽅式有很多, 但是整体可以分成两⼤类: 对称加密 和 ⾮对称加密。
2.1 🍎只使用对称加密🍎
如果通信双⽅都各⾃持有同⼀个密钥X,且没有别⼈知道,这两⽅的通信安全当然是可以被保证的。
但是这样做有一个很大的弊端,客户端有很多,如果服务器要维护每一个客户端的密钥那么代价是不是太大了呢?所以这种方式是行不通的。
我们可以换一种思路:密钥通过通信双方来协商,但是这样做又会有一个致命的问题,双方协商密钥时中间人可以通过某种方式来获取该密钥,那不是密文跟明文没有区别了吗?
所以只使用对称加密方式是行不通的。
2.2 🍎只使用非对称加密🍎
鉴于⾮对称加密的机制,如果服务器先把公钥以明⽂⽅式传输给浏览器,之后浏览器向服务器传数据
前都先⽤这个公钥加密好再传,从客户端到服务器似乎是安全的(ps:这里可能是有安全问题),因为只有服务器有相应的私钥能解开公钥加密的数据。
但是服务器到浏览器的这条路怎么保障安全?这条路中间人完全可以窃取公钥,当浏览器向服务器传输报文时就使用窃取的公钥解密,这样从浏览器向服务器发送的数据就都被窃取了。
所以只使用非对称加密方式是行不通的。
2.3 🍎双方都使用非对称加密🍎
- 1️⃣服务端拥有公钥S与对应的私钥S’,客户端拥有公钥C与对应的私钥C’;
- 2️⃣客户和服务端交换公钥;
- 3️⃣客户端给服务端发信息:先⽤S对数据加密,再发送,只能由服务器解密,因为只有服务器有私钥S’;
- 4️⃣服务端给客户端发信息:先⽤C对数据加密,在发送,只能由客⼾端解密,因为只有客⼾端有私钥C.
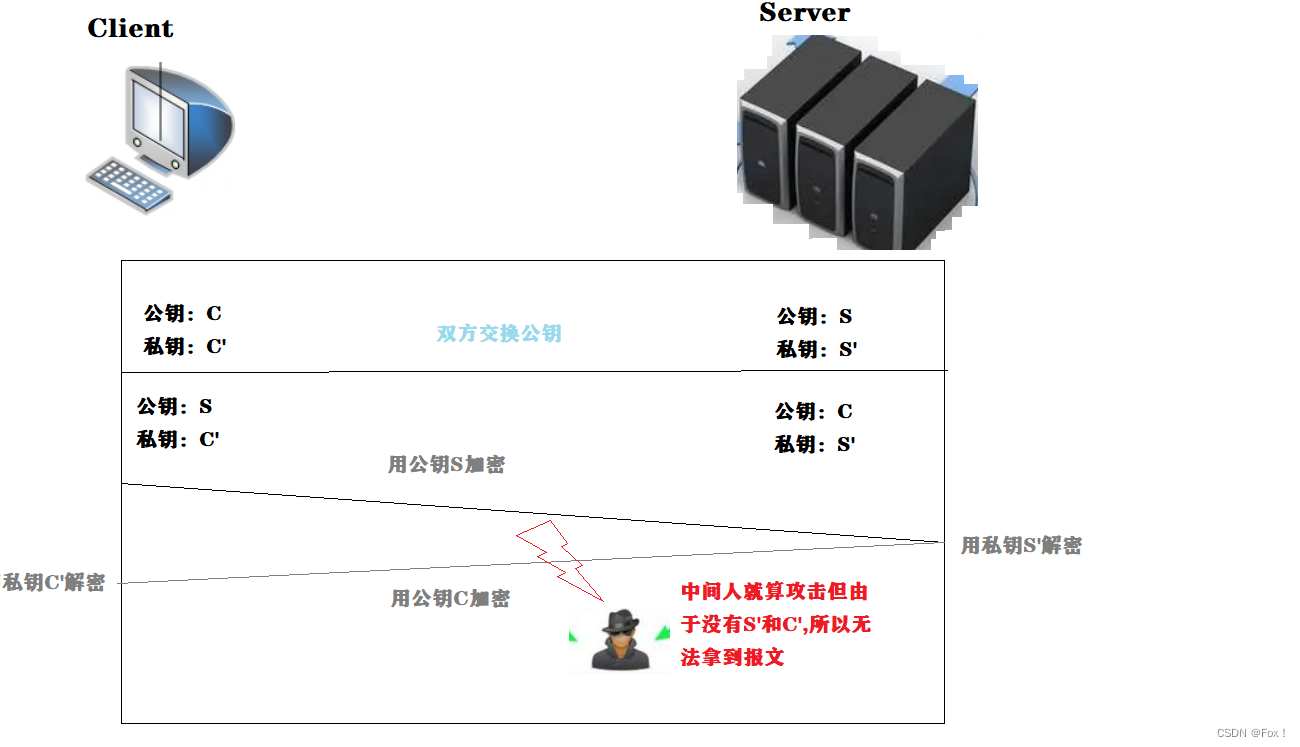
这样貌似也⾏啊,但是效率太低,依旧有安全问题(ps:这个安全问题我们放在后面统一讲解)
2.4 🍎非对称加密 + 对称加密🍎
首先来解决效率问题:
- 1️⃣服务端具有非对称公钥S和私钥S’,客户端发起https请求,获取服务端公钥S;
- 2️⃣客户端在本地⽣成对称密钥C, 通过公钥S加密, 发送给服务器;由于中间的⽹络设备没有私钥, 即使截获了数据, 也⽆法还原出内部的原⽂, 也就⽆法获取到对称密钥。(ps:这里也有可能会有安全问题)
- 3️⃣服务器通过私钥S’解密, 还原出客户端发送的对称密钥C. 并且使⽤这个对称密钥加密给客户端返回的响应数据.后续客户端和服务器的通信都只⽤对称加密即可. 由于该密钥只有客户端和服务器两个主机知道, 其他主机/设备不知道密钥即使截获数据也没有意义。
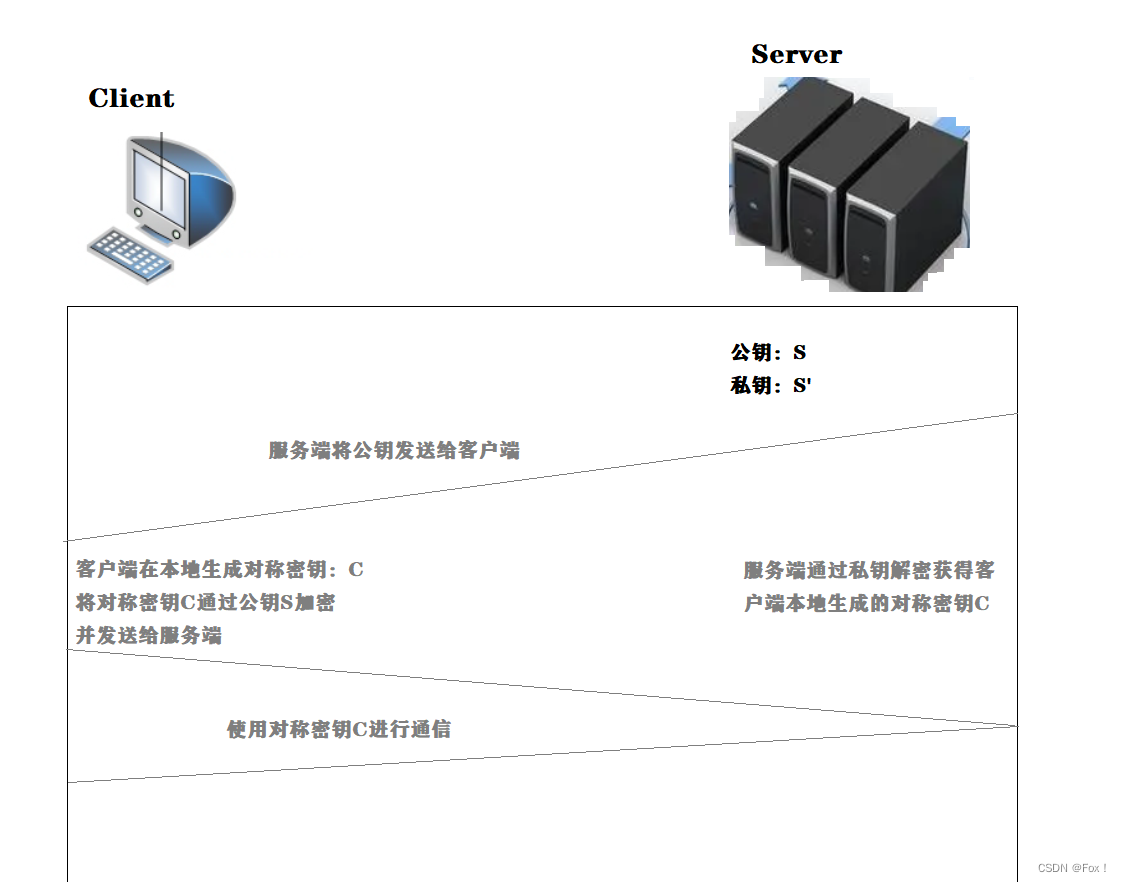
这样我们后续通信只用对称密钥C进行,就大大增加了通信的效率。
但是我们还遗漏了一个问题:如果服务器将公钥S发送给客户端时有中间人将公钥替换了呢?
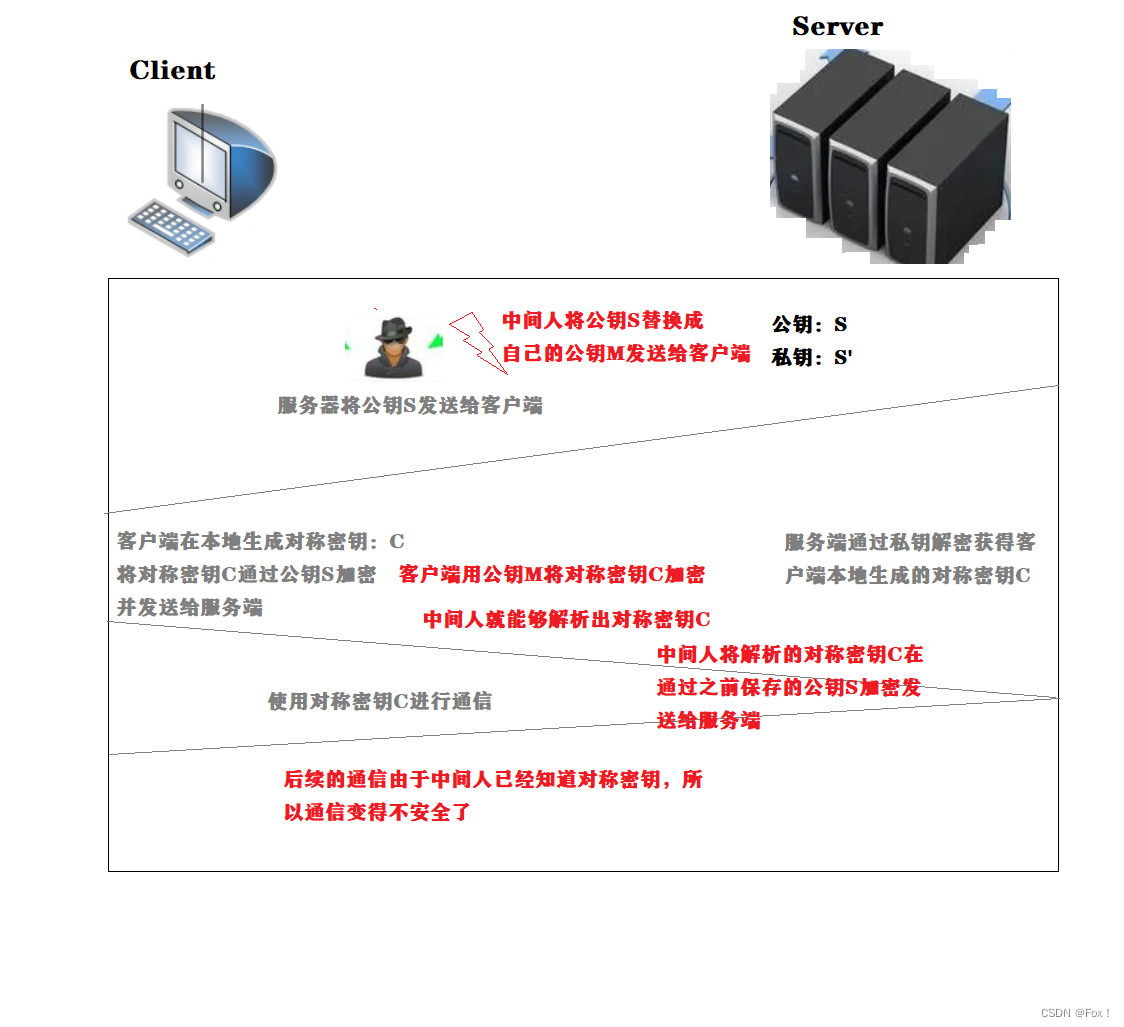 不仅仅是在这里,在双方都使用非对称加密那里也存在着这样的问题:其本质原因都是因为:
不仅仅是在这里,在双方都使用非对称加密那里也存在着这样的问题:其本质原因都是因为:客户端⽆法确定收到的含有公钥的数据报⽂,就是⽬标服务器发送过来的.
所以就引入了我们下面介绍的证书。
3 🍑证书🍑
3.1 🍎CA认证🍎
服务端在使⽤HTTPS前,需要向CA机构申领⼀份数字证书,数字证书⾥含有证书申请者信息、公钥信息等。服务器把证书传输给浏览器,浏览器从证书⾥获取公钥就⾏了,证书就如⾝份证,证明服务端公钥的权威性。
这个证书可以理解成是⼀个结构化的字符串, ⾥⾯包含了以下信息:
- 证书发布机构
- 证书有效期
- 公钥
- 证书所有者
- 签名等等
需要注意的是:申请证书的时候,需要在特定平台⽣成查,会同时⽣成⼀对密钥对,即公钥和私钥。这对密钥对就是⽤来在⽹络通信中进⾏明⽂加密以及数字签名的。其中公钥会随着CSR⽂件,⼀起发给CA进⾏权威认证,私钥服务端⾃⼰保留,⽤来后续进⾏通信(其实主要就是⽤来交换对称秘钥)
3.2 🍎数据签名🍎
签名的形成是基于⾮对称加密算法的,注意,⽬前暂时和https没有关系,不要和https中的公钥私钥搞
混了。
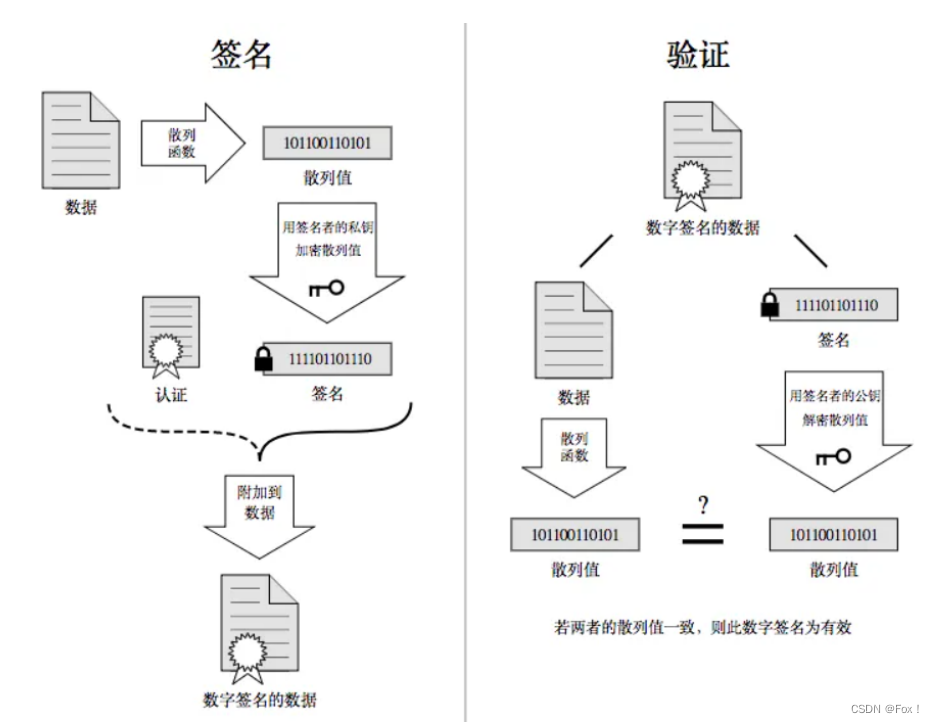 当服务端申请CA证书的时候,CA机构会对该服务端进⾏审核,并专⻔为该⽹站形成数字签名,过程如
当服务端申请CA证书的时候,CA机构会对该服务端进⾏审核,并专⻔为该⽹站形成数字签名,过程如
下:
- 1️⃣ CA机构拥有非对称加密的私钥A和公钥A’;
- 2️⃣ CA机构对服务端申请的证书明⽂数据进⾏hash,形成数据摘要;
- 3️⃣ 然后对数据摘要⽤CA私钥A’加密,得到数字签名S.
服务端申请的证书明⽂和数字签名S共同组成了数字证书,这样⼀份数字证书就可以颁发给服务端了.(ps:图中名词签名者就是指的是CA机构)
3.3 🍎非对称加密 + 对称加密 + 证书认证🍎
在客户端和服务器刚⼀建⽴连接的时候, 服务器给客户端返回⼀个证书,证书包含了之前服务端的公钥, 也包含了⽹站的⾝份信息.
客户端进⾏认证:
当客户端获取到这个证书之后, 会对证书进⾏校验,防⽌证书是伪造的:
- 判定证书的有效期是否过期;
- 判定证书的发布机构是否受信任(操作系统中已内置的受信任的证书发布机构);
- 验证证书是否被篡改: 从系统中拿到该证书发布机构的公钥, 对签名解密, 得到⼀个 hash 值(称为数据摘要), 设为 hash1. 然后计算整个证书的 hash值, 设为hash2. 对⽐hash1和hash2是否相等. 如果相等, 则说明证书是没有被篡改过的。
3.4 🍎常见问题🍎
3.4.1 🍋中间人有没有可能篡改该证书?🍋
中间⼈篡改了证书的明⽂,由于他没有CA机构的私钥,所以⽆法hash之后⽤私钥加密形成签名,那么也就没法办法对篡改后的证书形成匹配的签名;如果强⾏篡改,客户端收到该证书后会发现明⽂和签名解密后的值不⼀致,则说明证书已被篡改,证书不可信,从⽽终⽌向服务器传输信息,防⽌信息泄露给中间⼈。
3.4.2 🍋中间人有没有可能整个掉包证书?🍋
因为中间⼈没有CA私钥,所以⽆法制作假的证书。所以中间⼈只能向CA申请真证书,然后⽤⾃⼰申请的证书进⾏掉包,这个确实能做到证书的整体掉包,但是别忘记,证书明⽂中包含了域名等服务端认证信息,如果整体掉包,客户端依旧能够识别出来。中间⼈没有CA私钥,所以对任何证书都⽆法进⾏合法修改。
3.4.3 🍋为什么摘要内容在网络传输的时候⼀定要加密形成签名?🍋
常⻅的摘要算法有: MD5 和 SHA 系列。
以 MD5 为例, 我们不需要研究具体的计算签名的过程, 只需要了解 MD5 的特点:
- 定⻓: ⽆论多⻓的字符串, 计算出来的 MD5 值都是固定⻓度 (16字节版本或者32字节版本)
- 分散: 源字符串只要改变⼀点点, 最终得到的 MD5 值都会差别很⼤.
- 不可逆: 通过源字符串⽣成 MD5 很容易, 但是通过 MD5 还原成原串理论上是不可能的
正因为 MD5 有这样的特性, 我们可以认为如果两个字符串的 MD5 值相同, 则认为这两个字符串相同。
假设我们的证书只是⼀个简单的字符串 hello, 对这个字符串计算hash值(比如md5), 结果为BC4B2A76B9719D91;如果 hello 中有任意的字符被篡改了, 比如变成了 hella, 那么计算的 md5 值就会变化很⼤:BDBD6F9CF51F2FD8。然后我们可以把这个字符串 hello 和 哈希值BC4B2A76B9719D91 从服务器返回给客户端, 此时客户端如何验证 hello 是否是被篡改过?
那么就只要计算 hello 的哈希值, 看看是不是 BC4B2A76B9719D91 即可。
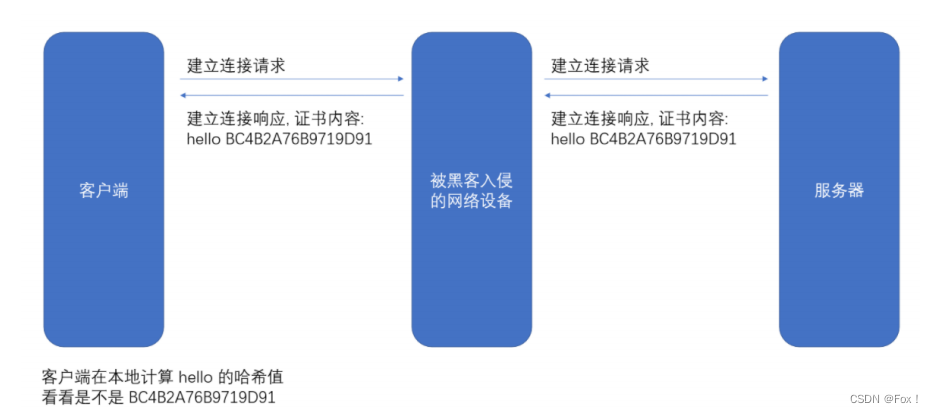
但是还有个问题, 如果⿊客把 hello 篡改了, 同时也把哈希值重新计算下, 客户端就分辨不出来了呀。
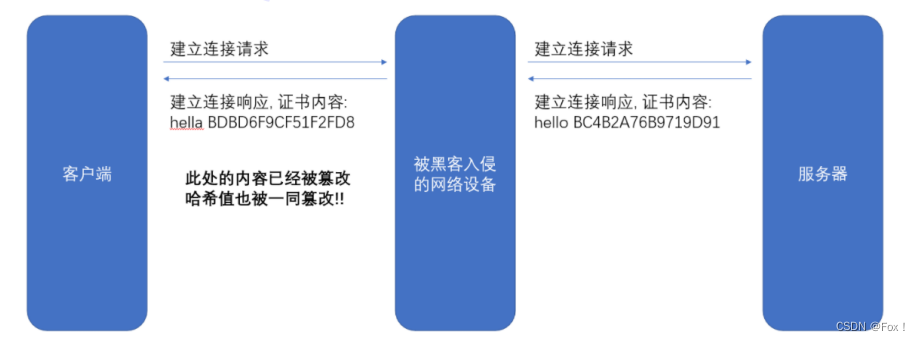 所以被传输的哈希值不能传输明⽂, 需要传输密⽂。
所以被传输的哈希值不能传输明⽂, 需要传输密⽂。
所以,对证书明⽂(这⾥就是“hello”)hash形成散列摘要,然后CA使⽤⾃⼰的私钥加密形成签名,将hello和加密的签名合起来形成CA证书,颁发给服务端,当客户端请求的时候,就发送给客户端,中间⼈截获了,因为没有CA私钥,就⽆法更改或者整体掉包,就能安全的证明,证书的合法性。最后,客户端通过操作系统⾥已经存的了的证书发布机构的公钥进⾏解密, 还原出原始的哈希值, 再进⾏校验。
3.4.4 🍋为什么签名不直接加密,⽽是要先hash形成摘要?🍋
- 缩⼩签名密⽂的⻓度,加快数字签名的验证签名的运算速度。
4 🍑总结🍑
HTTPS ⼯作过程中涉及到的密钥有三组:
- 第⼀组(⾮对称加密): ⽤于校验证书是否被篡改. 服务器持有私钥(私钥在形成CSR⽂件与申请证书时获得), 客户端持有公钥(操作系统包含了可信任的 CA 认证机构有哪些, 同时持有对应的公钥). 服务器在客户端请求时,返回携带签名的证书. 客⼾端通过这个公钥进⾏证书验证, 保证证书的合法性,进⼀步保证证书中携带的服务端公钥权威性。
- 第⼆组(⾮对称加密): ⽤于协商⽣成对称加密的密钥. 客户端⽤收到的CA证书中的公钥(是可被信任的)给随机⽣成的对称加密的密钥加密, 传输给服务器, 服务器通过私钥解密获取到对称加密密钥.
- 第三组(对称加密): 客户端和服务器后续传输的数据都通过这个对称密钥加密解密.
其实⼀切的关键都是围绕这个对称加密的密钥. 其他的机制都是辅助这个密钥⼯作的.
- 第⼆组⾮对称加密的密钥是为了让客户端把这个对称密钥传给服务器;
- 第⼀组⾮对称加密的密钥是为了让客户端拿到第⼆组⾮对称加密的公钥.