特征工程 是确定哪些特征可能对训练模型有用,然后通过转换日志文件等数据来源中的原始数据来创建这些特征的过程。在本文中,笔者将重点讨论何时以及如何转换数字和分类数据,以及不同方法的权衡。
目录
1.数据转换的原因
1.1 数据兼容性的强制转换
1.2 可选的质量转换
2.去哪里转换?
2.1 训练前转型
2.2 在模型内进行转换
3.探索、清理和可视化您的数据
4.转换数字数据
4.1 为什么要规范化数字特征?
4.2 规范化-Normalization
4.2.1 标准化技术概览
4.2.2 缩放到一定范围
4.2.3 特征剪裁
4.2.4 对数缩放
4.2.5 Z 分数
4.2.6 概括
4.3 分桶
4.3.1 分位数分桶
4.3.2 分桶总结
5.转换分类数据
5.1 词汇
5.1.1 关于稀疏表示的注意事项
5.2 词汇外 (OOV)
5.3 散列
5.4 哈希和词汇的混合
5.5 关于嵌入的注意事项
6.参考文献
1.数据转换的原因
我们改造特征主要出于以下原因:
1.1 数据兼容性的强制转换
- 将非数字特征转换为数字特征。由于无法对字符串进行矩阵乘法,因此我们必须将字符串转换为某种数字表示形式。
- 将输入大小调整为固定大小。线性模型和前馈神经网络具有固定数量的输入节点,因此输入数据必须始终具有相同的大小。例如,图像模型需要将数据集中的图像重塑为固定大小。
1.2 可选的质量转换
- 文本特征的标记化或小写。
- 标准化数字特征(大多数模型可以获得更好的表现)。
- 允许线性模型将非线性引入特征空间。
严格来说,质量转换不是必需的 ——模型在没有质量转换的情况下仍然可以运行。但使用这些技术可以使模型给出更好的结果。
2.去哪里转换?
我们可以在磁盘上或模型内生成数据时进行转换。
2.1 训练前转型
在这种方法中,我们在训练之前执行转换。该代码与机器学习模型分开。
优点
- 计算仅执行一次。
- 计算可以查看整个数据集来确定转换。
缺点
- 需要在预测时重现转换,谨防数据倾斜!
- 任何转换更改都需要重新运行数据生成,从而导致迭代速度变慢。
对于涉及在线服务的情况,倾斜更为危险。在离线服务中,我们也许还能够重用生成训练数据的代码。在在线服务中,创建数据集的代码和用于处理实时流量的代码几乎必然是不同的,这使得很容易引入偏见-Bias。
2.2 在模型内进行转换
对于这种方法,转换是模型代码的一部分。该模型采用未转换的数据作为输入,并将在模型内对其进行转换。
优点
- 轻松迭代。即使更改转换,仍然可以使用相同的数据文件。
- 保证在训练和预测时进行相同的转换。
缺点
- 昂贵的转换会增加模型延迟。
- 转换是按批次进行的。
每批次转换有很多考虑因素。假设你想要 通过平均值对特征进行归一化——即更改特征值以使其具有均值和标准差。在模型内部进行转换时,这种标准化将只能访问一批数据,而不是完整的数据集。你可以通过批次内的平均值进行标准化(如果批次差异很大,则很危险),或者预先计算平均值并将其固定为模型中的常量。我们将在下一节中探讨标准化。
3.探索、清理和可视化您的数据
在对数据执行任何转换之前探索并清理数据。在收集和构建数据集时,通常应完成了以下任务:
- 检查几行数据。
- 检查基本统计数据。
- 修复缺失的数字条目。
数据可视化。 图表可以帮助我们发现数值统计中不清楚的异常或模式。因此,在进行深入分析之前,请通过散点图或直方图以图形方式查看数据。不仅可以在训练开始时查看图形,还可以在整个转换过程中查看图形。可视化将帮助我们不断检查并了解任何重大变化的影响。
关于数据可视化,可以看一下《Python 数据可视化》,其中有详细的解读。
4.转换数字数据
在实际应用中,我们通常需要对数值数据进行如下两种类型的转换:
- 规范化:将数值数据转换为与其他数值数据相同的比例。
- 分桶:将数字(通常是连续的)数据转换为分类数据。
4.1 为什么要规范化数字特征?
笔者强烈建议对那些明显具有不同范围(例如年龄和收入,数值范围就有显著差异)的数字特征进行标准化。当不同的特征具有不同的范围时,梯度下降会 “反弹” 并减慢收敛速度。Adagrad 和Adam 等优化器通过为每个特征创建单独的有效学习率来防止此问题。
此外,建议对涵盖广泛范围的单个数字特征进行标准化,例如“城市人口”。如果不标准化“城市人口”特征,训练模型可能会生成 NaN 错误(Not a Number, 0 作为除数时会出现 NaN 错误,比如 10 / 0)。不幸的是,当单个特征中存在广泛的值时,像 Adagrad 和 Adam 这样的优化器无法防止 NaN 错误。
4.2 规范化-Normalization
规范化的目标是将特征转换为相似的尺度,从而提高模型的性能和训练稳定性。
4.2.1 标准化技术概览
四种常见的规范化技术如下:
- 缩放到一定范围
- 剪裁
- 对数缩放
- z 分数
下图显示了每种规范化技术对左侧原始特征(价格)分布的影响。这些图表基于 1985 年 Ward 汽车年鉴的数据集,该年鉴是UCI 机器学习存储库汽车数据集的一部分。
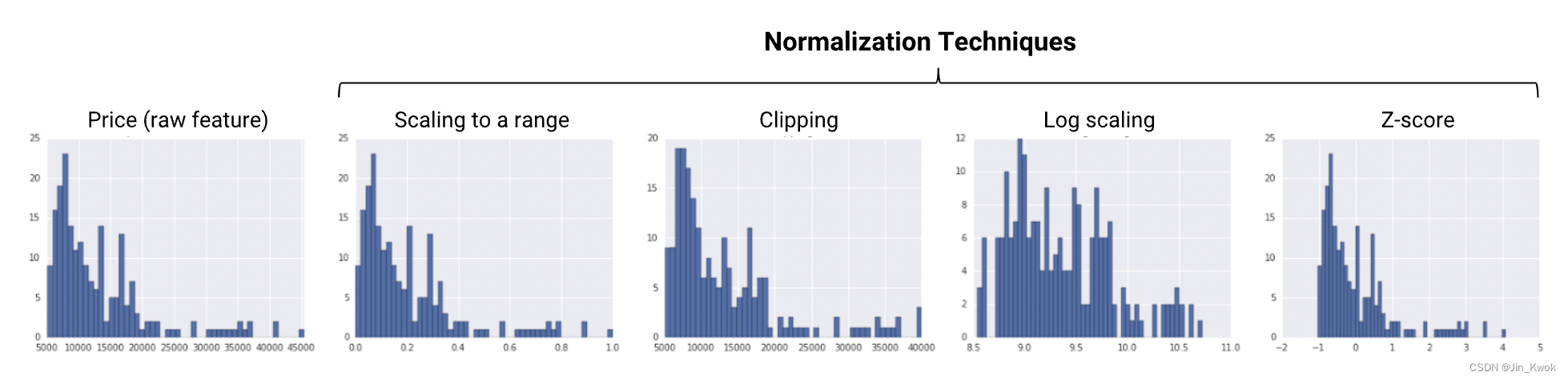 图 1. 标准化技术总结
图 1. 标准化技术总结
4.2.2 缩放到一定范围
即将浮点特征值从其自然范围(例如 100 到 900)转换为标准范围——通常为 0 和 1(或有时为 -1 到 +1)。使用以下简单公式缩放到一个范围:
当满足以下两个条件时,缩放到某个范围是一个不错的选择:
- 已知数据的大致上限和下限,很少或没有异常值。
- 数据在该范围内大致均匀分布。
一个很好的例子就是年龄。大多数年龄值在 0 到 90 之间,并且该范围的每个部分都有相当多的人。再来看一个反例,收入数据使用缩放就很不合适,因为只有少数人有很高的收入。收入线性规模的上限会非常高,大多数人会被挤进规模的一小部分。
4.2.3 特征剪裁
如果数据集包含极端异常值,则可以尝试特征裁剪,它将高于(或低于)特定值的所有特征值限制为固定值。例如,可以将所有高于 40 的温度值修剪为正好 40。你可以在其他标准化之前或之后应用特征裁剪。
公式:设置最小/最大值以避免异常值。
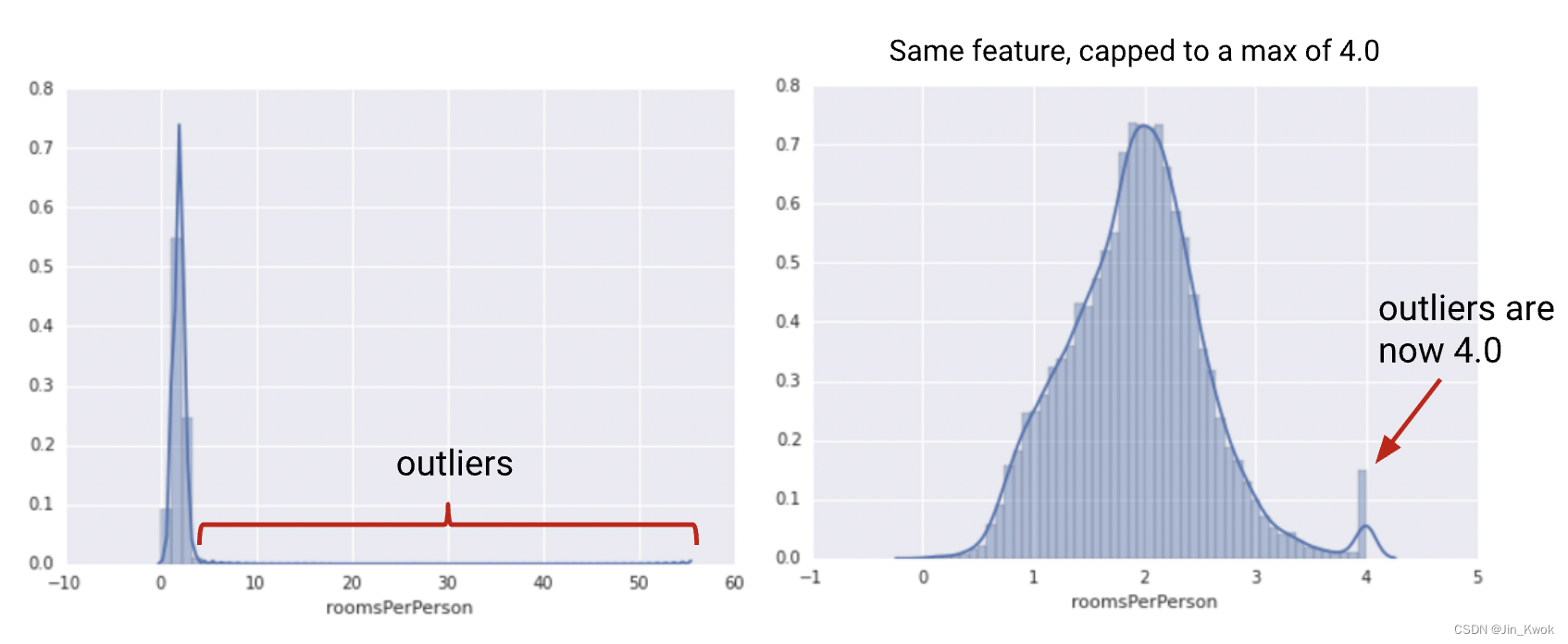
图 2. 比较原始发行版及其剪辑版本
另一种简单的裁剪策略是按 z 分数裁剪到 +-Nσ(例如,限制为 +-3σ)。请注意,σ是标准差。
4.2.4 对数缩放
对数缩放计算值的对数,将大范围压缩到窄范围。
当少数值有很多点(示例),而大多数其他值只有很少点时,对数缩放会很有帮助。这种数据分布称为 幂律分布。电影分级就是一个很好的例子。在下面的图表中,大多数电影的评分很少(尾部的数据),而少数电影的评分很高(头部的数据)。对数缩放会改变分布,有助于提高线性模型性能。
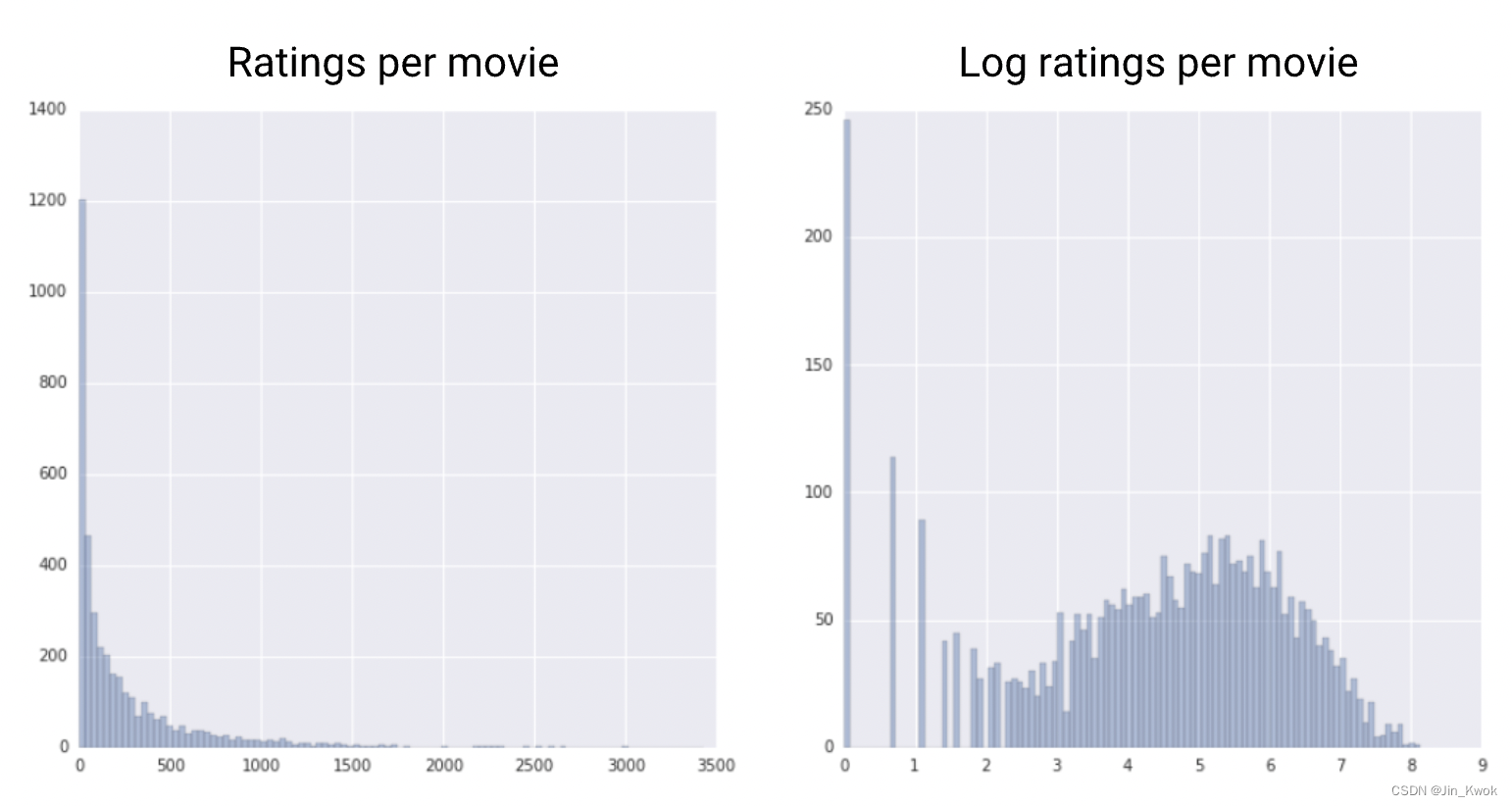
图 3. 将原始分布与其日志进行比较
4.2.5 Z 分数
Z 分数是缩放的一种变体,表示偏离平均值的标准差数。可以使用 Z 分数来确保特征分布的平均值 = 0 且标准差 = 1。当存在一些异常值时,它很有用,但又不会极端到需要裁剪。计算点 x 的 Z 分数的公式如下:
注:μ 为平均值,σ 为标准差。
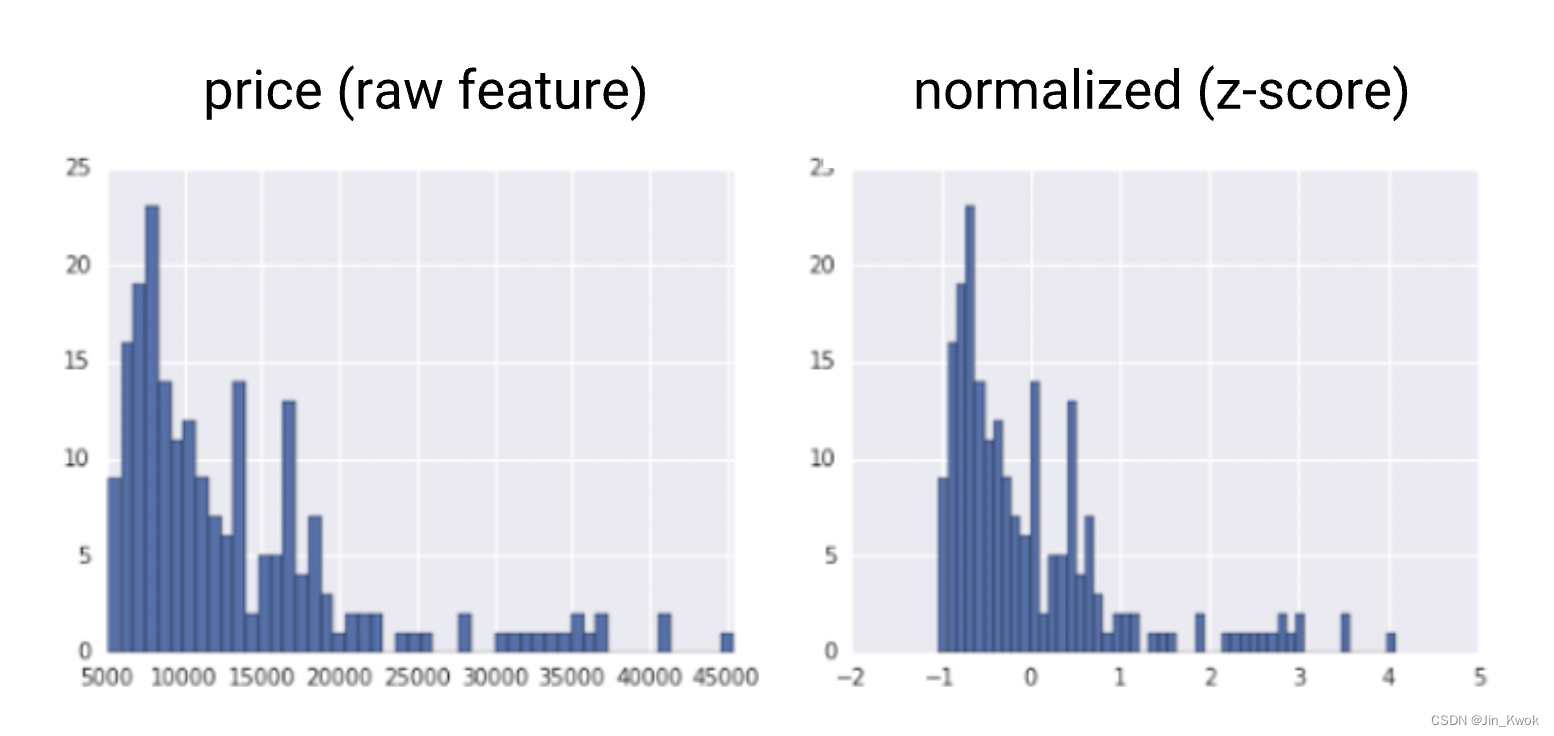
图 4. 将原始分布与其 z 分数分布进行比较
请注意,Z 分数将范围约为 40000 的原始值压缩为大约 -1 到 +4 的范围。
在某些情况下,我们可能不确定异常值是否真的极端,此时可以从 Z 分数开始。
4.2.6 概括
最好的规范化技术是一种在经验上效果良好的技术,在实践中,如果你发现新的方法对你的特征分布很有效,那么,不妨尝试新的方法。
| 规范化技术 | 公式 | 何时使用 |
|---|---|---|
| 线性缩放 | | 当特征或多或少均匀分布在固定范围内时。 |
| 剪裁 | 如果 x > max,则 x' = max。如果 x < 分钟,则 x' = 分钟 | 当特征包含一些极端异常值时。 |
| 对数缩放 | x' = log(x) | 当特征符合幂律时。 |
| Z 分数 | x' = (x - μ) / σ | 当特征分布不包含极端异常值时。 |
4.3 分桶
在前面的系列文章中,笔者已经介绍过“分桶”这一思想,这里再简单回顾一下,如图 5 中的分布情况。
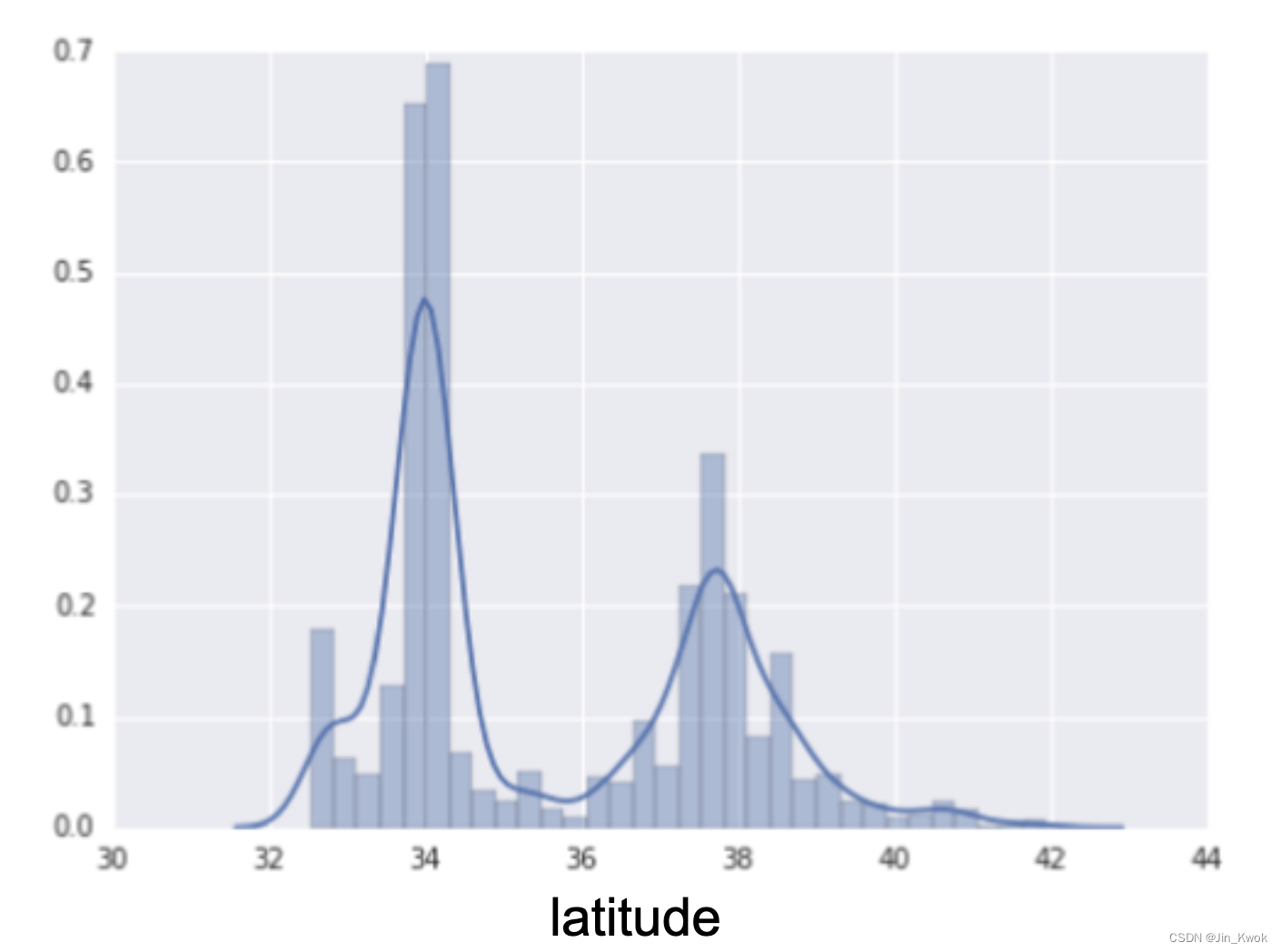
图 5:房价与纬度的关系
如图 5 所示,如果纬度可能是住房价值的良好预测指标,那么是否应该将纬度保留为浮点值?为什么或者为什么不?(假设这是一个线性模型。)
答案是否定的,从图 5 中可以看出,纬度和住房价值之间不存在线性关系。那么,保存浮点值(相较于整数,更加精确)是没有意义的。
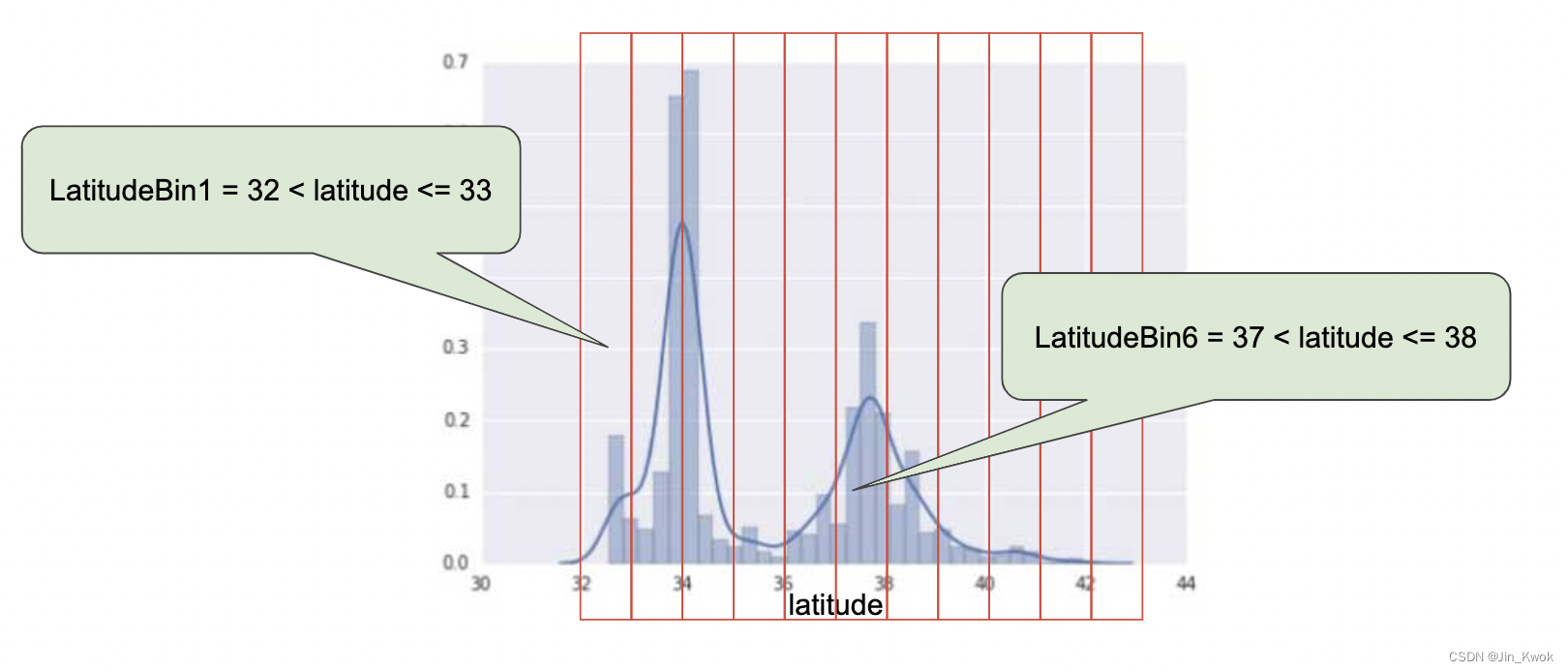
图 6:房价与纬度的关系,现在分为不同的桶
4.3.1 分位数分桶
如图 7 所示,是一个添加了分桶的汽车价格数据集。对于每个分桶中的特征,该模型对 >45000 范围内的示例(仅仅只有 1 个示例)使用的容量与 5000-10000 范围内的所有示例使用的容量一样多。这看起来很浪费。我们该如何改善这种情况呢?
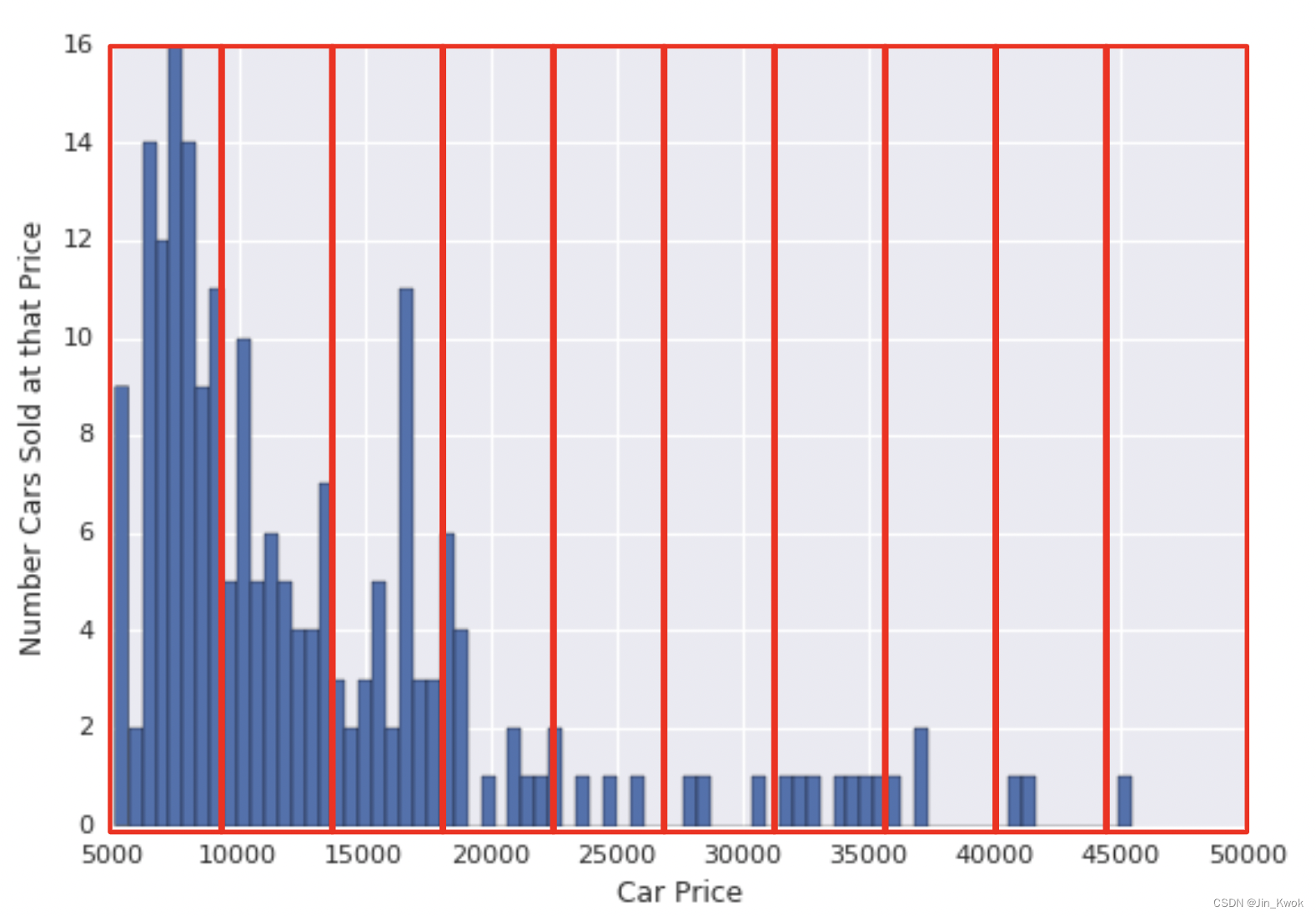
图 7:以不同价格出售的汽车数量
根本原因在于等距的桶不能很好地捕捉这种分布。解决方案在于创建每个具有相同点数的桶。这种技术称为 分位数分桶。如图 8 所示,将汽车价格划分为分位数桶。为了在每个桶中获得相同数量的示例,一些桶包含较窄的价格范围,而另一些则包含非常宽的价格范围。

图 8:分位数分桶为每个桶提供了大约相同数量的汽车
4.3.2 分桶总结
如果选择对数字特征进行分桶,首先需明确如何设置边界以及要应用哪种类型的分桶:
- 具有等距边界的桶:边界是固定的并且包含相同的范围(例如,0-4 度、5-9 度和 10-14 度,或 $5,000-$9,999、$10,000-$14,999 和 $15,000-$19,999)。有些桶可能包含很多点,而另一些桶可能包含很少的点或没有。
- 具有分位数边界的桶:每个桶具有相同数量的点。边界不是固定的,可以包含窄范围或宽范围的值。
等距边界分桶是一种适用于大量数据分布的简单方法。但是,对于倾斜数据,请尝试使用分位数分桶进行分桶。
5.转换分类数据
某些特征可能无序的离散值。例如狗的品种、单词或邮政编码。这些特征称为分类特征 ,每个值称为一个类别。我们可以将分类值表示为字符串甚至数字,但无法比较这些数字或将它们相互减去。
通常,应该将包含整数值的特征表示为分类数据而不是数字数据。例如,值为整数的邮政编码特征。如果错误地用数字表示此特征,那么就是在要求模型查找不同邮政编码之间的数字关系;例如,你希望模型确定邮政编码 20004 是邮政编码 10002 信号的两倍(或一半),显然这很荒谬!!!!通过将邮政编码表示为分类数据,则可以使模型为每个邮政编码查找单独的信号。
如果数据字段的类别数量较少,例如一周中的某一天或有限的调色板,您可以为每个类别创建一个单独的特征。例如:

图 9:每个类别的独特特征
然后,模型可以学习每种颜色的单独权重。例如,模型也许可以了解到红色汽车比绿色汽车更贵然后可以对这些特征进行索引。
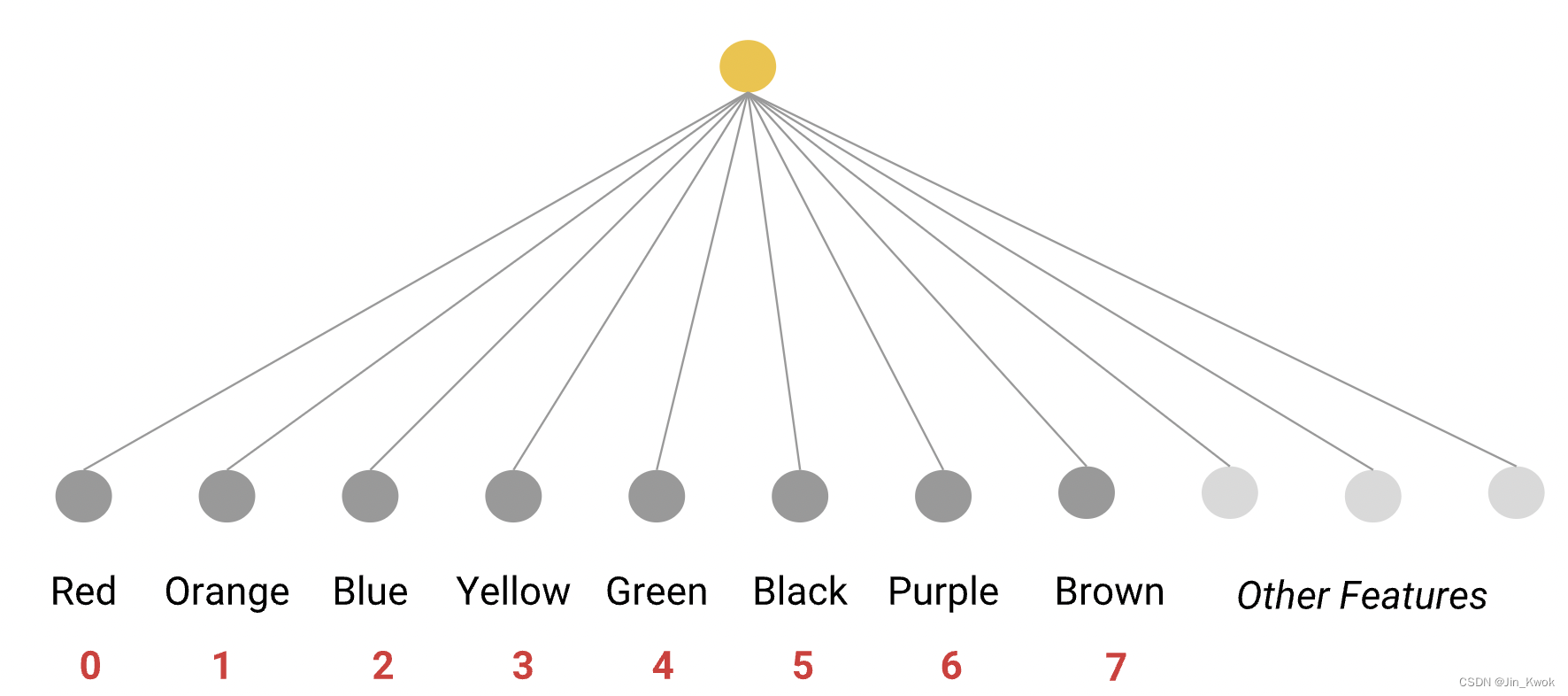
图 10:索引特征
这种映射称为词汇表。
5.1 词汇
在词汇表中,每个值代表一个独特的特征。
Index Number | Category |
|---|---|
0 | Red |
1 | Orange |
2 | Blue |
... | ... |
该模型从字符串中查找索引,将 1.0 分配给特征向量中的相应槽,将 0.0 分配给特征向量中的所有其他槽。

图 11:将类别映射到特征向量的端到端过程
5.1.1 关于稀疏表示的注意事项
例如,如果类别是一周中的几天,那么最终可能会使用特征向量 [0, 0, 0, 0, 1, 0, 0] 来表示星期五。然而,大多数机器学习系统的实现都会在内存中用稀疏表示来表示这个向量。常见的表示形式是非空值及其相应索引的列表,例如,值 1.0,索引 [4]。这中表示方式可以让我们花费更少的内存来存储大量的 0,并允许更有效的矩阵乘法。就底层数学而言,[4] 相当于 [0, 0, 0, 0, 1, 0, 0]。
5.2 词汇外 (OOV)
正如数值数据包含异常值一样,分类数据也包含异常值。例如,考虑包含汽车描述的数据集。该数据集的特征之一可能是汽车的颜色。假设常见的汽车颜色(黑色、白色、灰色等)在此数据集中得到了很好的体现,并且你将它们中的每一种都划分为一个类别,以便可以了解这些不同的颜色如何影响价值。然而,假设该数据集包含少量具有奇怪颜色(紫红色、深褐色、鳄梨色)的汽车。你可以将它们归入一个名为 Out of Vocab ( OOV ) 的包罗万象的类别,而不是为每种颜色指定一个单独的类别。通过使用 OOV,系统不会浪费时间对每种稀有颜色进行训练。
5.3 散列
另一种选择是将每个字符串(类别)散列到可用索引空间中。散列通常会导致冲突,但依赖于模型学习同一索引中类别的一些共享表示,这对于给定问题非常有效。
对于重要术语,由于冲突,散列可能比选择词汇表更糟糕。另一方面,散列不需要组装词汇表,如果特征分布随着时间的推移发生很大变化,这将是有利的。
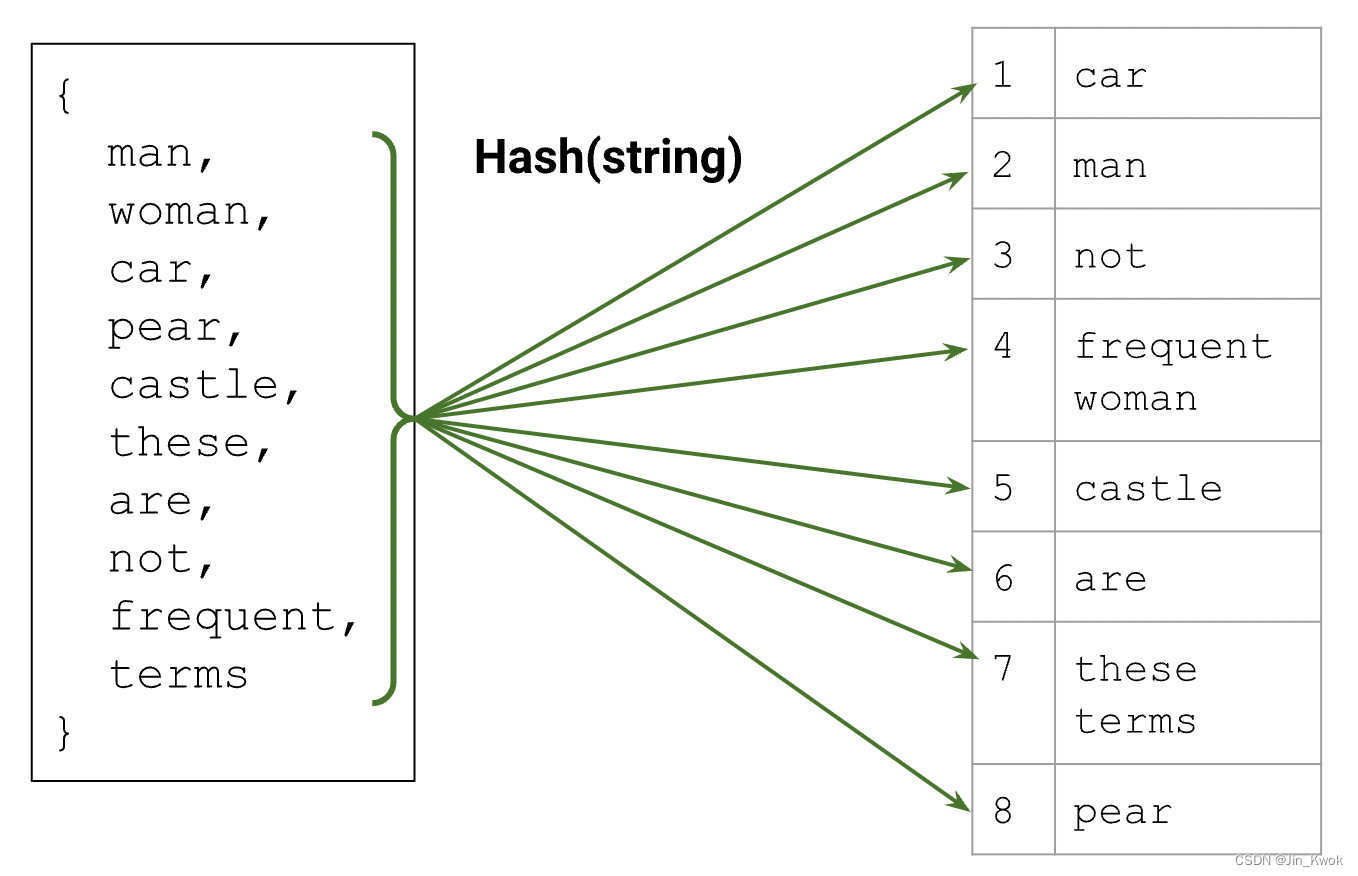
图 12:将项目映射到词汇表
5.4 哈希和词汇的混合
可以采用混合方法,将哈希与词汇表结合起来,对数据中最重要的类别使用词汇表,但将单一 OOV 存储桶替换为多个 OOV 存储桶,并使用散列将类别分配给存储桶。
哈希桶中的类别必须共享一个索引,并且模型可能无法做出良好的预测,但我们已经分配了一定量的内存来尝试学习词汇表之外的类别。
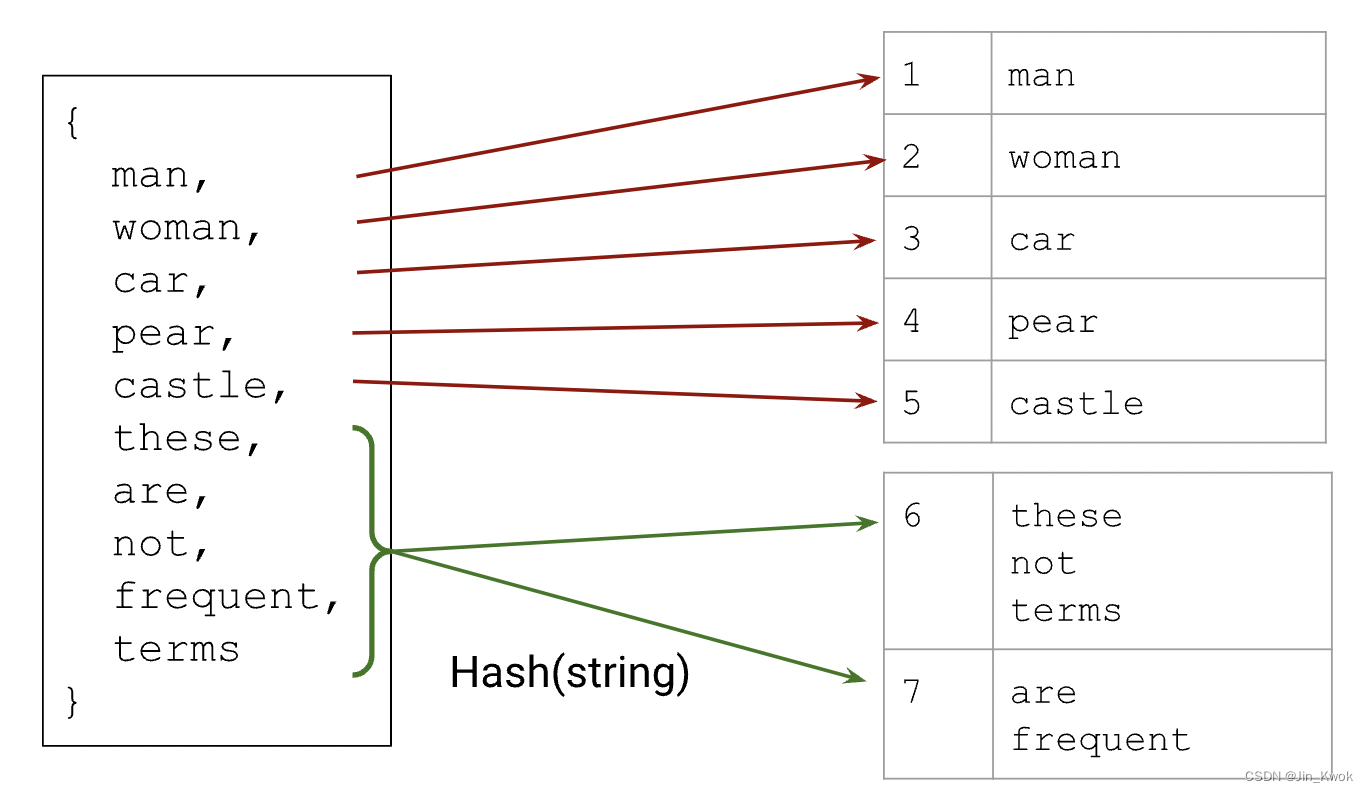
图 13:结合词汇和散列的混合方法
5.5 关于嵌入的注意事项
在《机器学习20:嵌入-Embeddings》中已经介绍过嵌入,这里简单回顾一下,嵌入表示为连续值特征的分类特征。深度模型经常将索引从索引转换为嵌入。
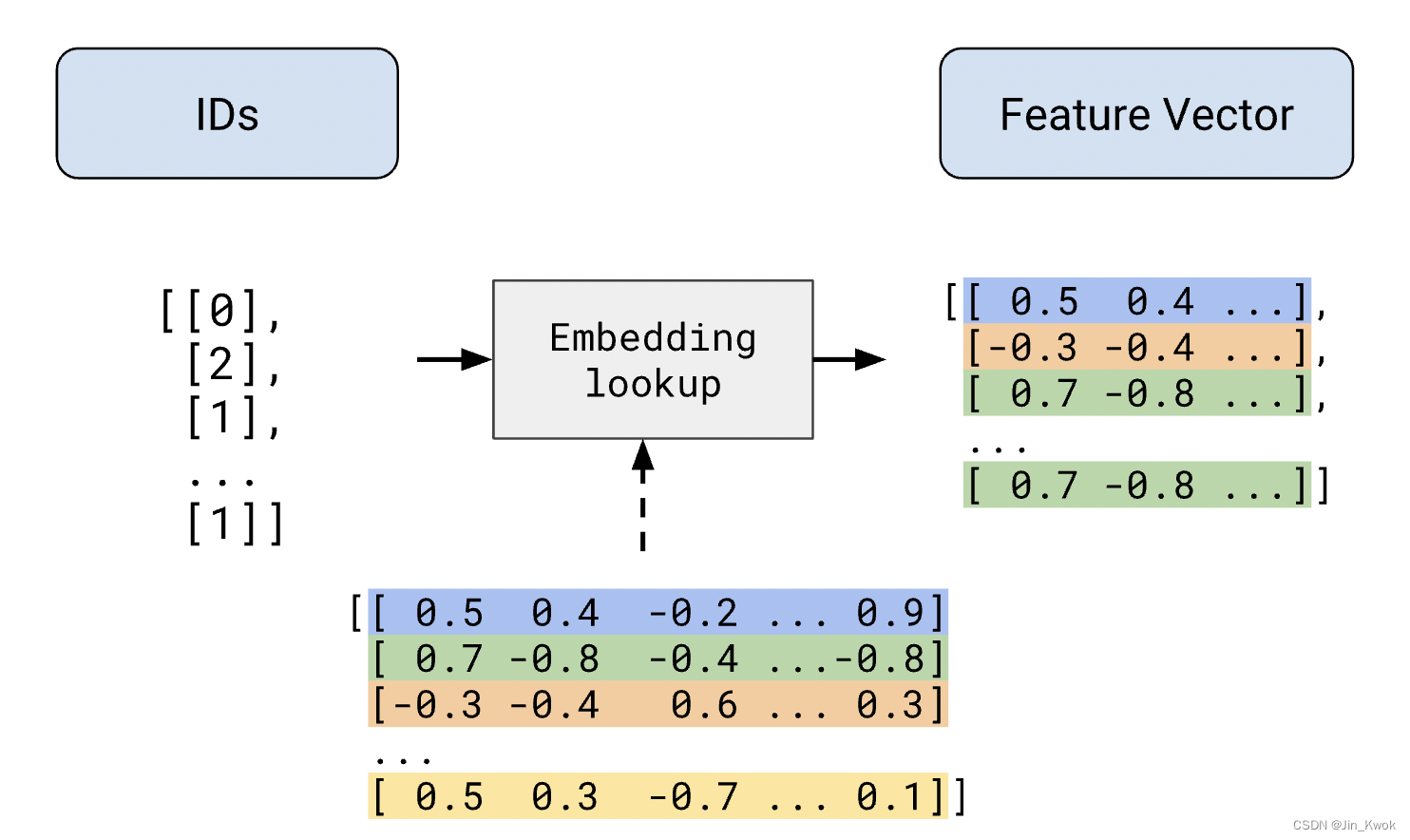
图 14:通过嵌入的稀疏特征向量
我们讨论的其他转换可以存储在磁盘上,但嵌入不同。由于嵌入是经过训练的,因此它们不是典型的数据转换——它们是模型的一部分。它们使用其他模型权重进行训练,在功能上相当于一层权重。
预训练嵌入怎么样?预训练的嵌入通常在训练期间仍然可以修改,因此它们在概念上仍然是模型的一部分。
6.参考文献
链接-https://developers.google.cn/machine-learning/data-prep/transform/transform-categorical