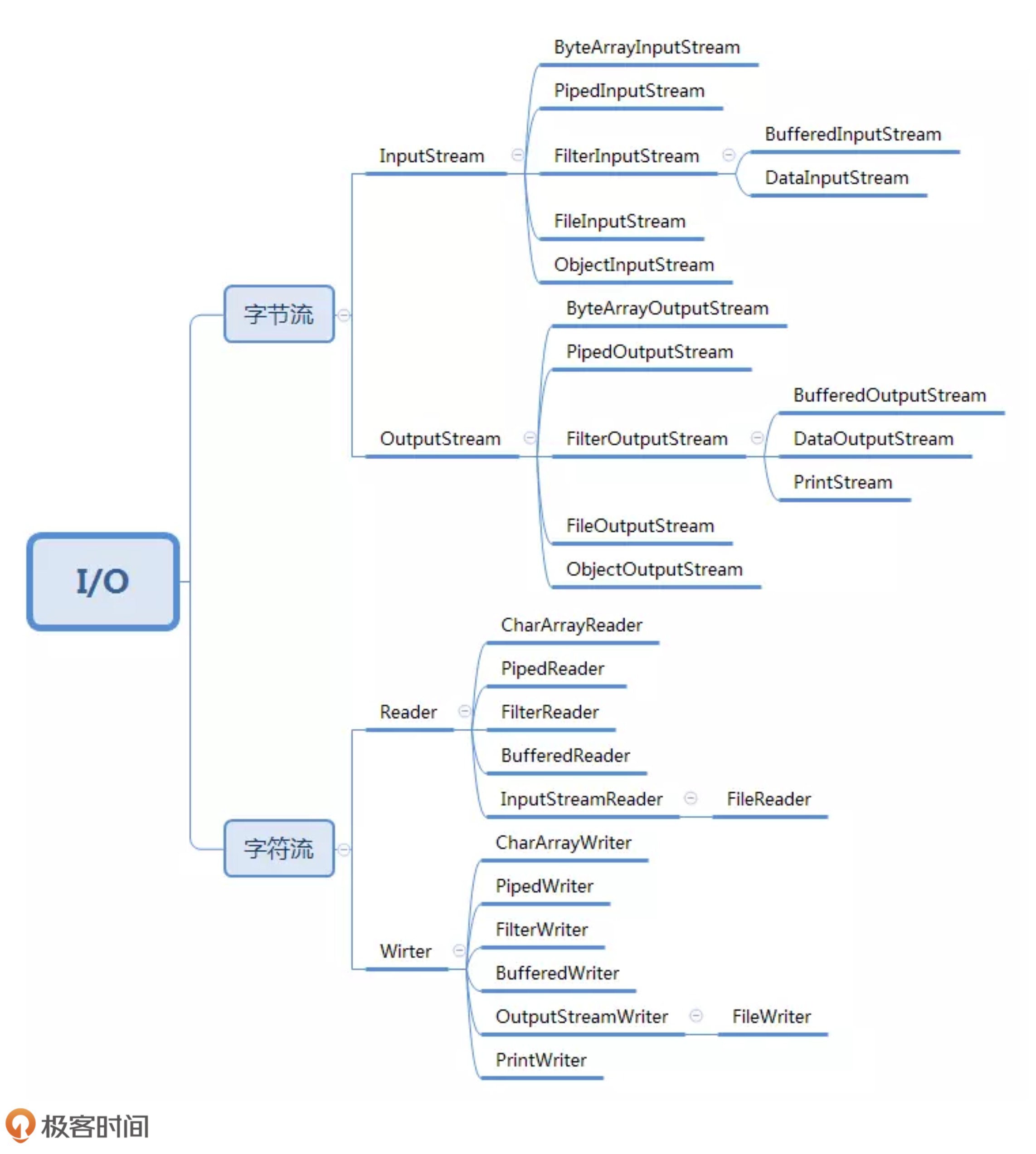
文章目录
- 53.最大子数组和
- 枚举思路
- 暴力解法
- 贪心思路
- 完整版
- 时间复杂度
- 122.买卖股票的最佳时机Ⅱ(解法比较巧妙)
- 思路
- 完整版
- 总结
53.最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
- 1 <=
nums.length<= 10^5 - -10^4 <=
nums[i]<= 10^4
枚举思路
本题的暴力解法就是两个for循环,一个for循环遍历子数组,一个for循环用来计算当前数值对应的所有子数组的和,枚举所有的和,最后返回最大值。
暴力解法
class Solution {
public:int maxSubArray(vector<int>& nums) {int result = INT_MIN;int sum=0;for(int i=0;i<nums.size();i++){//求所有以i为开头的子数组的和for(int j=i;j<nums.size();j++){sum += nums[j];result = result>sum?result:sum;}//遍历完一个数字之后重置sumsum=0;}return result;}
};
暴力解法逻辑比较简单,但是超时了
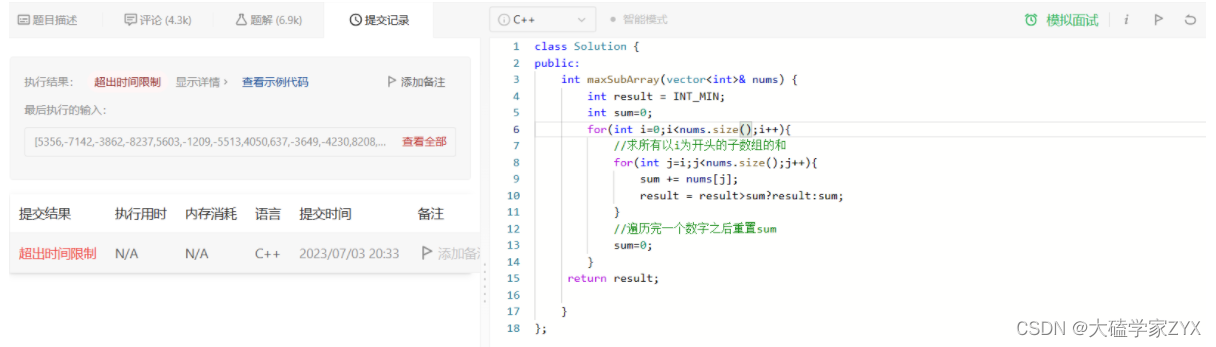
贪心思路
因为这个题目数组里面有负数,负数累加只会让值变得更小。因此,与其使用-2,不如重新开始,以新的位置作为连续和的起点。
局部最优就是,当求解连续和为负数的时候,立刻抛弃,因为负数只会影响总和。全局最优就是找到最大子数组的和。
注意,只是连续和是负数的时候就抛弃,不是遇到负数就抛弃!因为示例可以看到,很有可能最后的结果,本来就是带有负数的!
只要连续和不是负数,就往后加,因为正数对后面的数一定有增大作用。result会记录到目前为止的最大值,因此不需要担心前面的正数或者较大的总和被漏掉的情况。
贪心策略如下图所示。只要连续和是负数,负数一定没有正面作用,就立刻抛弃,选择下一个位置为起点。
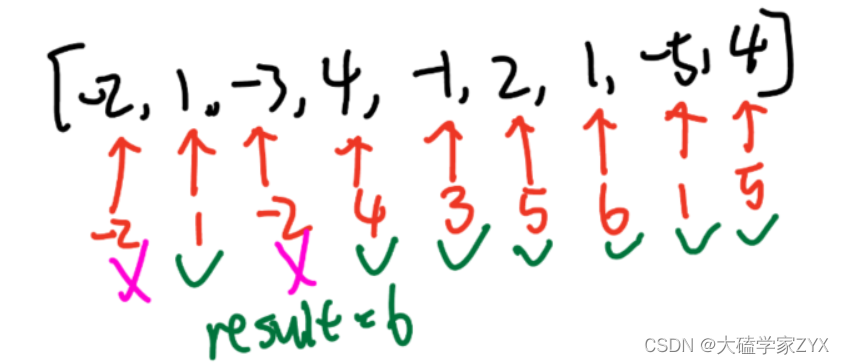
完整版
- 注意舍弃负数的情况,不需要改变for循环起始位置,只需要sum置零,就算是重新开始计数了
- 题目没有说如果数组为空,应该返回什么,所以数组为空的话返回什么都可以
class Solution {
public:int maxSubArray(vector<int>& nums) {int result=INT_MIN;int sum=0;for(int i=0;i<nums.size();i++){sum+=nums[i];//先给result赋值,收集所有最大值防止全是负数result = result>sum?result:sum;//如果遇到负数if(sum<0){//如果<0,不需要改变for循环起始位置,直接sum赋值成0,就是从下一个重新开始计数!sum=0;}}return result;}
};
时间复杂度
- 时间复杂度:O(n)
- 空间复杂度:O(1)
122.买卖股票的最佳时机Ⅱ(解法比较巧妙)
- 本题解法很巧妙,接触过之后要记住这种解法,即隔几天售卖的总利润和每天利润累加实质上是相等的!
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。
提示:
1 <= prices.length <= 3 * 10^40 <= prices[i] <= 10^4
思路
本题为什么会考虑用贪心来做,就是因为任意两天的利润差值,都可以进行拆分,拆成每相邻两天利润差值的和。
示例如下图所示:
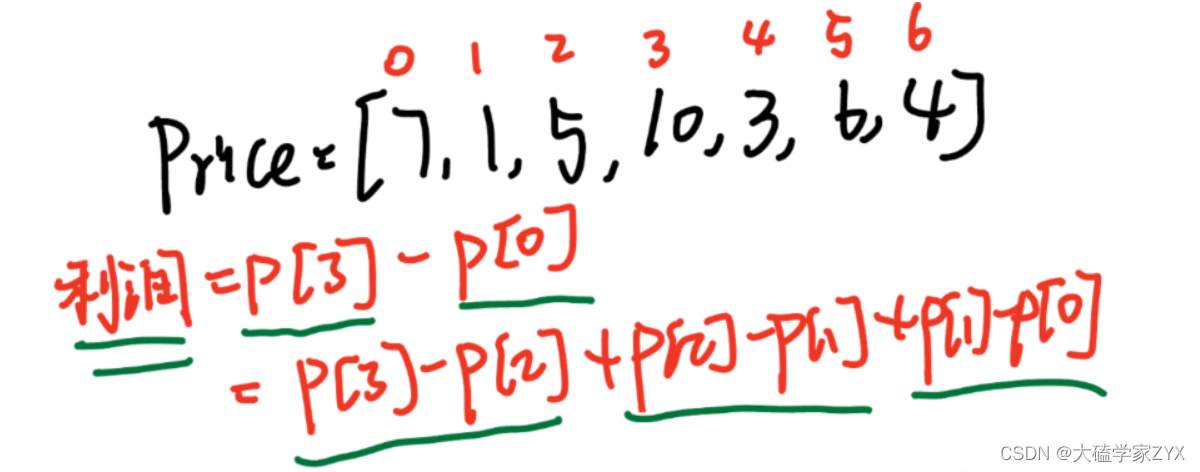
此时,拆成了相邻两天的差值,思路就和上一道题比较类似了。
如果想要总利润变大,遇到利润为负数的时候,需要立刻舍弃,然后在下一个新起点开始重新计数。我们只尝试收集正的利润。示意图如下:

本题的情况,任何时候只能持有一支,但是可以多次买卖,也就是说只要在所有相邻元素后-前的结果中,全部收获正数,就可以获取最大收益。
贪心策略:局部最优就是遇到正数就收集,全局最优就是结果最大。
完整版
class Solution {
public:int maxProfit(vector<int>& prices) {int result=0;int count=0;for(int i=0;i<prices.size()-1;i++){count = prices[i+1]-prices[i];if(count>0){result+=count;}}return result;}
};
总结
这道题用的是一种非常巧妙的思路,把利润分解为每天为单位的维度,而不是从 0 天到第 3 天整体去考虑。把问题转换成相邻数字的差累加最大值的问题,就很好写了。
本题中理解利润拆分是关键点! 不要整块的去看,而是把整体利润拆为每天的利润。
因为1–3天整体的利润和1–3天每天的利润累加,在数学上就是一个恒等式!
贪心的问题就是没接触过会很难想到,接触过之后,下次遇到这种情形,就可以考虑这样的解法了。