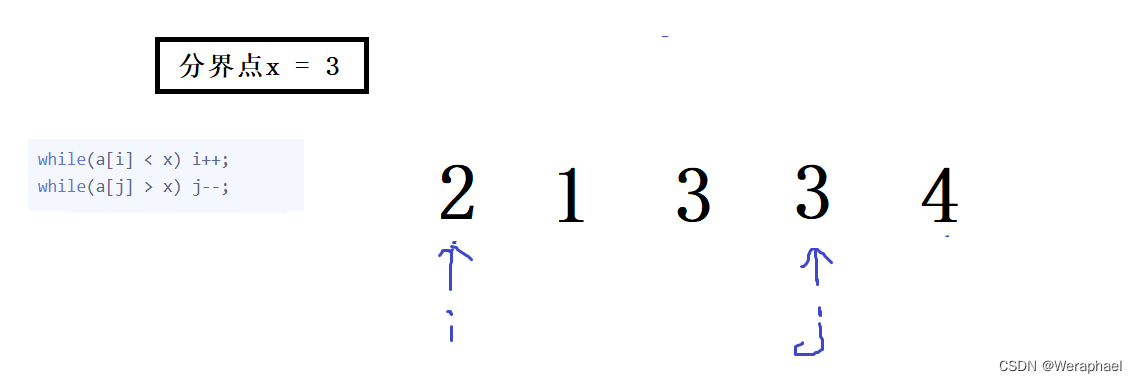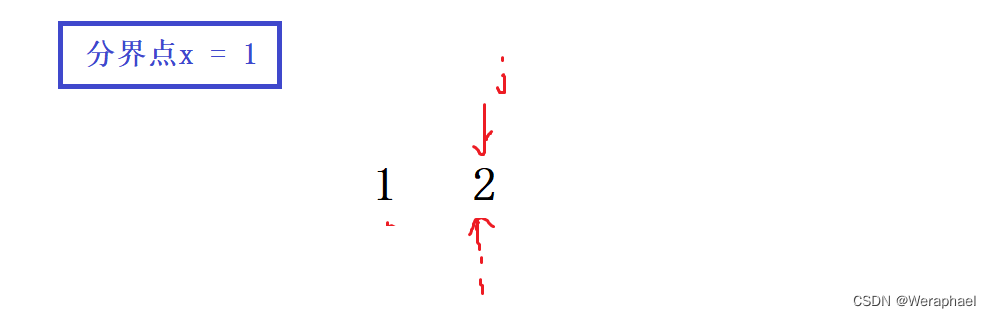👦个人主页：Weraphael
✍🏻作者简介：目前正在学习c++和算法
✈️专栏：【C/C++】算法
🐋 希望大家多多支持，咱一起进步！😁
如果文章有啥瑕疵
希望大佬指点一二
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注😍

---

一、快速排序步骤

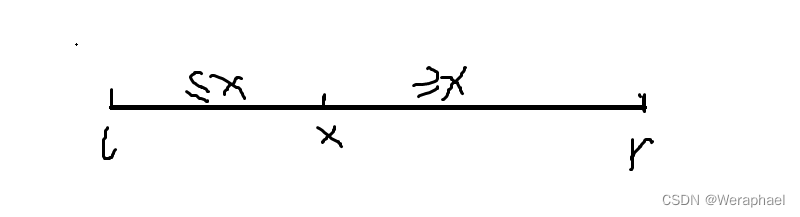
1. 第一步：要确定一个分界点x。分界点可以取左端a[0]、右端a[n - 1]、中间值a[(l+r) / 2]或者是随机值
2. 第二步：调整区间。快速排序的思想是分治。 所以，要使分界点左部分≤x，右部分≥x （升序）。
3. 第三步：递归处理左右两个部分。

Q：如何将数组一分为二，使≤x在左边，≥x在右边呢？

法一：暴力做法

1. 开辟两个数组分别是c[]、q[]。
2. 再扫描原数组a[]，把≤x的元素放在c[]中，≥x放在q[]中。
3. 最后先将c[] 放入a[]，再把b[]放入a[]。

法二：双指针做法（推荐）

1. 首先先让指针i++向中间寻找元素，直到指向的a[i] ≥x停下
2. 同样地，再将指针 j - -向中间寻找元素，直到指向的a[j] ≤x停下
3. 当条件满足 i < j，就将这两个元素交换（swap）
4. 当循环结束，指针j最终就一定会在指针i的前面

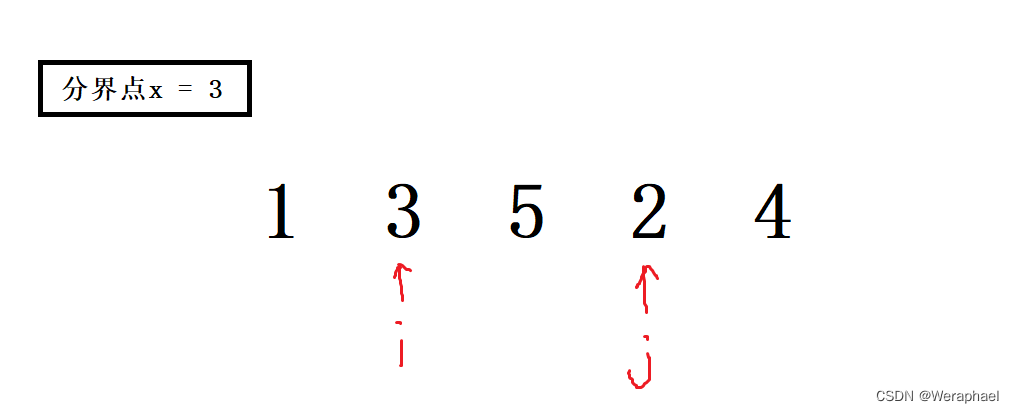
举个例子来验证双指针算法：

假设要升序排序 1 3 5 2 4，并设分界点x = 3

• 先移动i，直到i指向的元素≥3停下
  
• 再移动j，直到j指向的元素≤3停下​​
  ​​
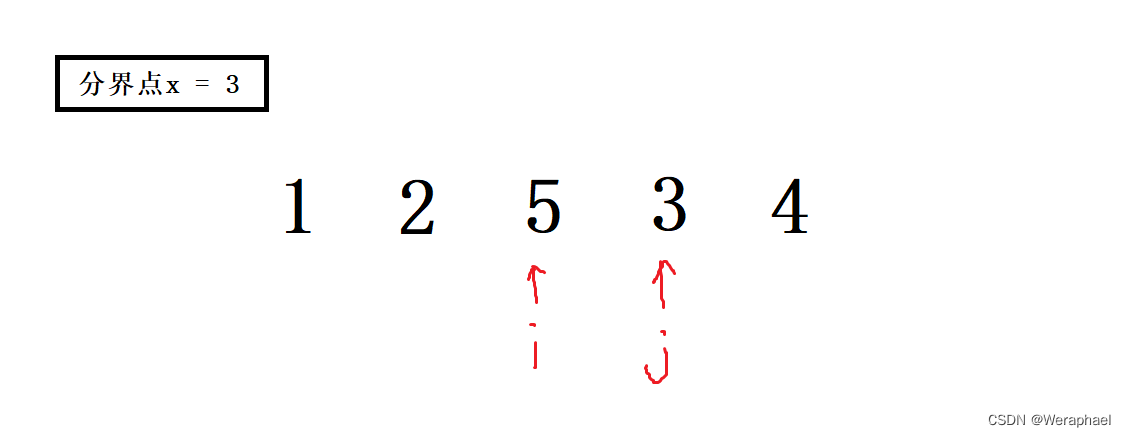
• 当条件满足i < j，则交换
  
• 接着继续移动i，直到i指向的元素≥3停下
  
• 再移动j ，直到j 指向的元素≤3停下
  
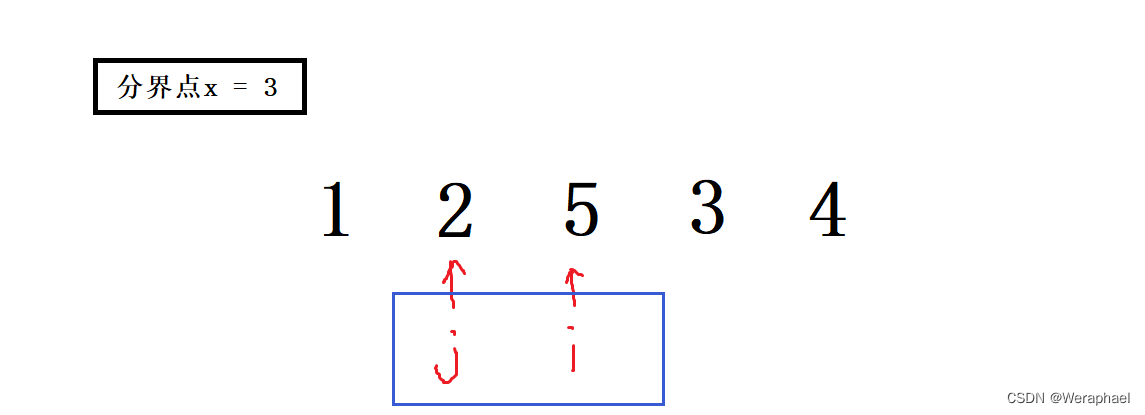
  最后，我们会发现，j最终停在了i的前面

二、代码模板

void quick_sort(int a[],int l,int r)
{// //如果数组中就一个数或者没有数，就没必要再排序(递归出口) if(l >= r) return; // 1. 确定分界点xint x = a[(l + r) / 2]; // 2. 调整区间// 将指针指向边界（边界问题）int i = l - 1, j = r + 1;while (i < j){do i++; while(a[i] < x);do j--; while(a[j] > x);if (i < j) swap(a[i],a[j]);}// 3. 递归处理左右两部分//递归处理左部分，也就是<x的部分quick_sort(a, l, j);//递归处理右部分，>x的部分quick_sort(a, j + 1, r);
}

三、边界问题

3.1 为什么要指针要指向边界，然后使用do while而不直接使用 while?

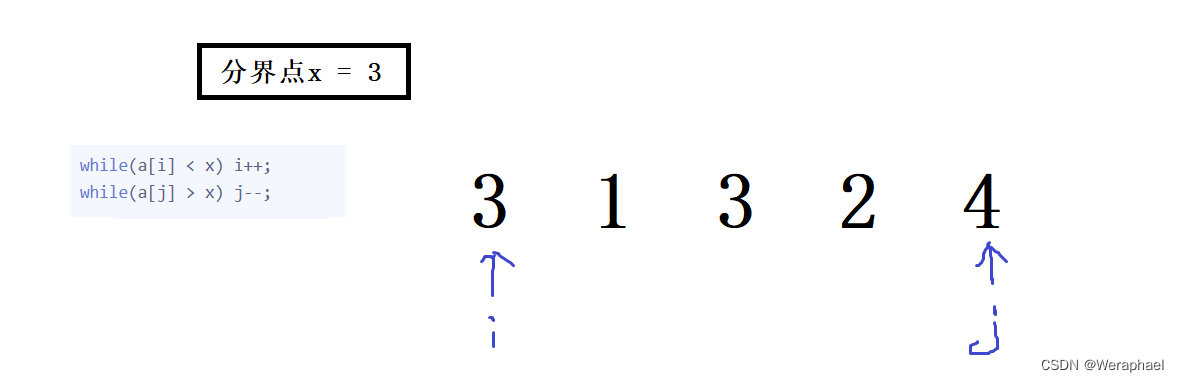
原因是：以while为例，假设数组中有 相同的元素，会发生死循环

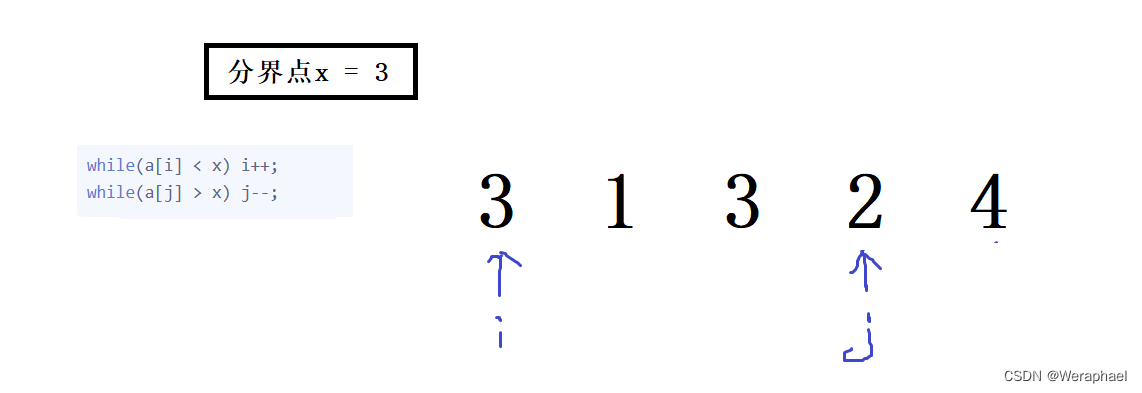
举个例子，假设排序 3 1 3 2 4，并设分界点x = 3

1. 先判断i
   
2. 再判断j
   
3. 当条件 i < j ，交换元素
   
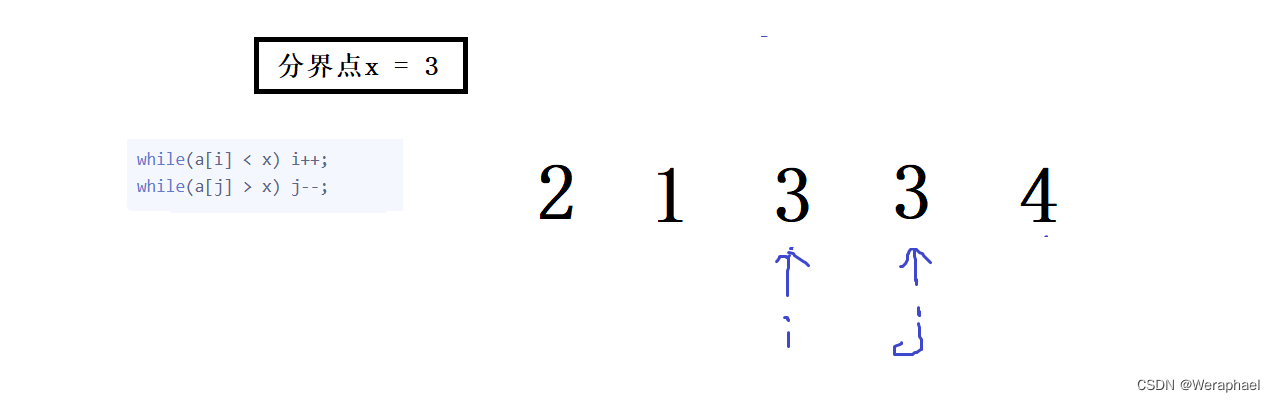
4. 接着再判断i ，而j不满足条件会继续指向3
   
   最后你会发现，就会一直死循环交换3

​

3.2 为什么移动移动i和j的条件分别是 < x 和 > x，而不是一开始所说的<= x和>= x

如果分界点x，恰好是数组中最大值，会导致越界。
同理，如果分界点又恰好是数组中最小值，也会导致越界。

3.3 当分界点为左端点x = a[0]

递归部分就不能使用quick_sort(a, l, i - 1)、quick_sort(a,i,r)，会导致 死递归
举个例子
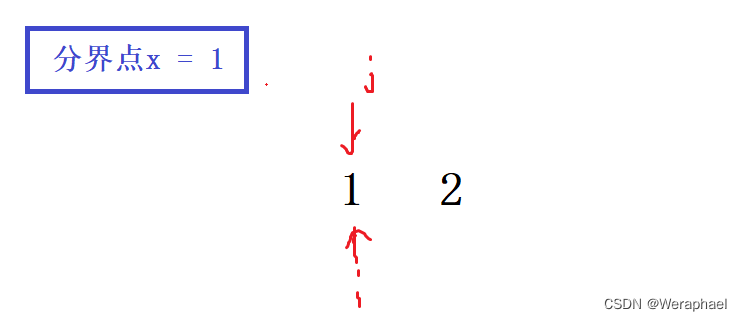
当数组只有1和2在排序时，左端点分界点x = 1

因此，到时候i和j会同时指向1
此时i = 0，j = 0，l = 0，r = 1
对于第一个递归：quick_sort(a,0,- 1)，相当于数组内没有值可以交换。
对于第二个递归：quick_sort(a, 0, 1)，这时，就一直就这两个数交换，导致死递归。

3.4 当分界点为右端点a[n - 1]

递归部分就不能使用quick_sort(a,l,j)、quick_sort(a,j + 1,r)，会导致 死递归
和例子3.3是一样的
当数组内部还是只有1和2两个元素，这时右端点x = 2

因此，到时候i和j会同时指向2
此时i = 1，j = 1，l = 0，r = 1
第一个递归quick_sort(a,0,1)，这时，就一直就这两个数交换，导致死递归

3.5 当x = a[(l + r) / 2]

递归部分不能使用quick_sort(a,l,i - 1)、quick_sort(a,i,r)
还是同样的例子，假设还是只有1和2在排序，这时分界点x = a[(0 + 1)/2] = a[0] = 1，这种情况就和3.3是一样的了。

3.6 当x = a[(l + r + 1) / 2]

递归部分就不能使用quick_sort(a,l,j)、quick_sort(a,j + 1,r)
还是同样的例子，数组还是只有1,2两个元素，这时分界点x = a[(0 + 1 + 1)/2] = a[1] = 2，这中情况就和3.4是一样的

四、算法分析

1. 时间复杂度
   快速排序最坏时间复杂度是O(n^2)，最好的时间复杂度为O(nlogn)

2. 空间复杂度
   空间复杂度是O(1)，因为没有用到额外开辟的集合空间。

3. 算法稳定性
   快速排序是不稳定的排序算法。因为我们无法保证相等的数据按顺序被扫描到和按顺序存放。

五、总结

1. 当x=a[l]或者x=a[(l + r) /2]，只能用

//左半部分递归
quick_sort(a, l, j); 
//右半部分递归
quick_sort(a,j + 1, r);

2. 当x=q[r] or x=q[l+r + 1>>1]，只能用

//左半部分递归
quick_sort(a,l,i - 1);
//右半部分递归
quick_sort(a, i, r);