生成对抗网络(Generative Adversarial Network, GAN)的原理
学习李宏毅机器学习课程总结。
前面学习了GAN的直观的介绍,现在学习GAN的基本理论。现在我们来学习GAN背后的理论。
引言
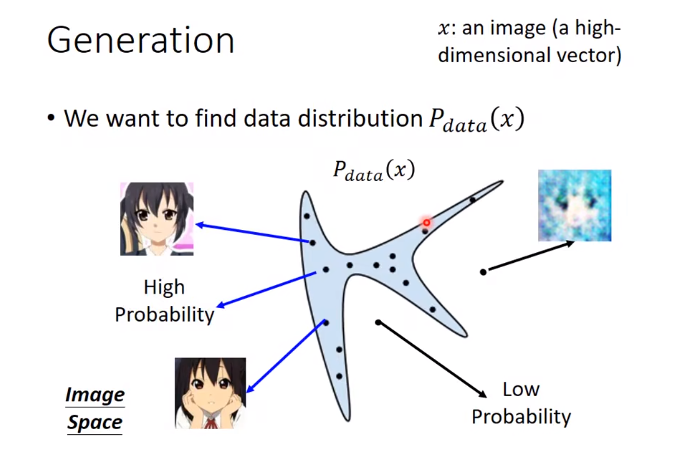
假设x是一张图片(一个高维向量),如64 * 64 * 3的图片,每个图片都是高维空间中的一个点。为了画图方便,我们就画成二维上的点。在高维空间中,只有一小部分采样出来的点符合我们的数据分布(如:整个图中只有蓝色区域采样的点的才是人脸,其他地方的就不是)。
我们想要产生的图片,其数据分布为Pdata。
目的: 让机器找出这个分布。
原始做法
在有GAN之前,人们怎么做生成任务呢?
最大似然估计 (Maximum likelihood estimate)。
- 假设数据集的数据分布为Pdata(x)
比如数据集为二次元人物,我们也不知道Pdata长什么样 - 假设生成数据分布为PG(x; θ)
希望找到θ,使得PG(x; θ)和原始未知分布Pdata(x)越接近越好
如:服从高斯分布,θ就是均值和方差 - 从Pdata(x)里采样一组样本{x1, x2, …, xm}
- 对每个样本,计算其似然:PG(xi; θ)
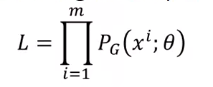
找到一个θ*,使得该似然值最大
下面有个很重要的概念:
最大似然估计 = 最小KL散度
下面证明:
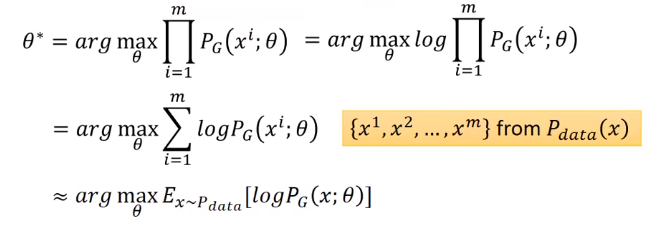
注:求最大值的θ,多个log不影响,为了乘积变加和
我们可以先回顾一下KL散度的定义:
设P(x)和Q(x) 是随机变量X 上的两个概率分布,则在离散随机变量的情形下,KL散度的定义为:
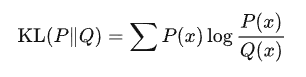
在连续随机变量的情形下,KL散度的定义为:
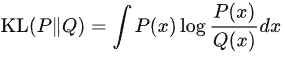
接着上面的,所以:
下面多加了一项(红框),对结果不影响对吧,是为了和KL散度有关。

所以,生成模型目的等价为:最小化分布PG和分布Pdata的散度。
如何定义一个广义的PG?
如果分布为简单的高斯分布,我们可以计算PG(x; θ),但实际数据都是更复杂的数据,有更复杂的分布,所以无法计算出PG的似然。怎么办?有人提出Generator。
GAN的做法
Generator
图像生成任务在80年代就有人做,那个时候人们就是用高斯模型做,但生成的图片非常非常模糊,不管怎么调整均值和方差,都出不来想要的结果。所以需要更广义的方法做生成任务,即生成对抗网络。
G怎么做生成呢?
从高斯分布中采样的数据z(也可以是其他分布,,如均匀分布等,那到底哪种分布输入好呢?其实都可以,对输出的影响不是很大,因为G都能给它变成更复杂的分布),输入网络G,得到输出x。
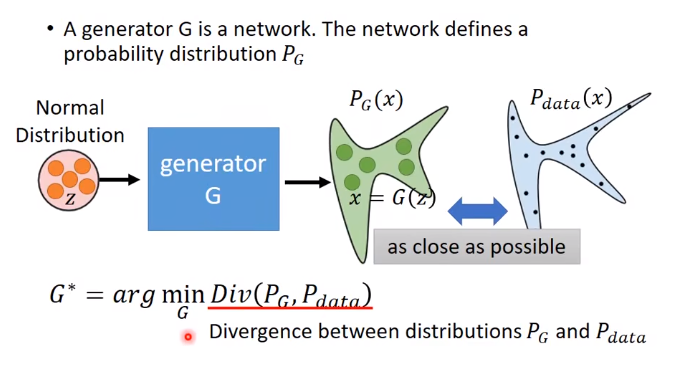
我们希望概率分布PG和Pdata越接近越好,也就是最小化它们的某种散度Divergency(有很多散度,不一定是KL散度)。
那怎么计算这个散度呢?
Pdata和PG的概率分布公式我们不知道,所以不知道怎么算。所以人们想到了判别器Discriminator。
Discriminator
虽然我们不知道Pdata和PG的概率分布公式,但我们可以从这两堆数据里分别采样一些出来。
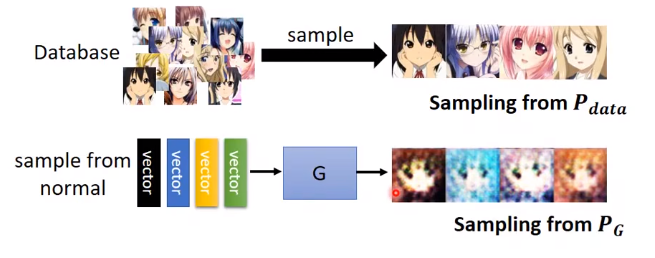
GAN的神奇之处就在于,可以通过D来量这两堆数据之间的散度。
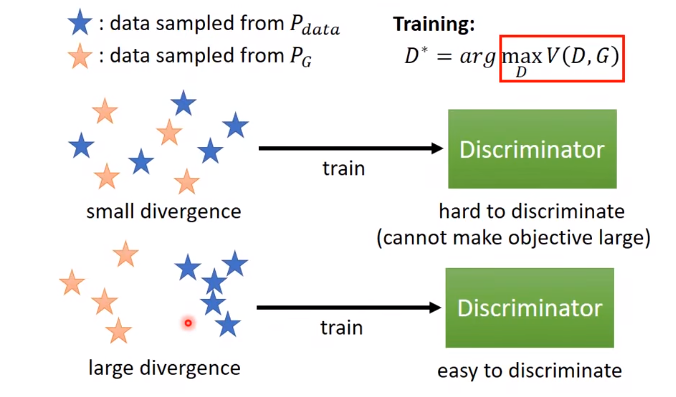
把从Pdata和PG分布里取出的样本数据输入D,训练:
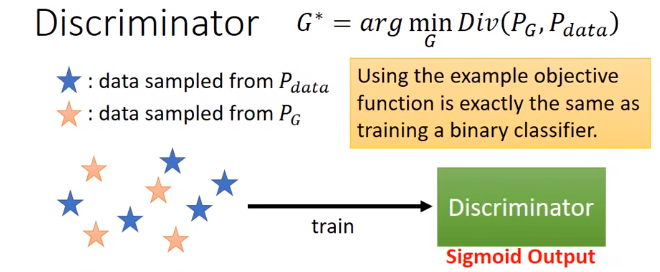
D相当于二分类器,希望对真数据Pdata,输出分数越大越好;对生成数据PG,输出分数越小越好。训练的D的结果,就会告诉我们PG和Pdata他们之间的散度有多大。
训D的时候,G的参数是固定住的。

如果你机器学习基础很好的话,就可以看出这个D的优化函数和二分类器的式子一模一样。
神奇的地方是,当你训完D,你可以得到一个最小的loss或最大的V(D, G ),而这个值和某个JS散度有一些关系,甚至可以说它就是JS散度。
如果D很难区别两类数据的不同,loss就下不去,目标函数就不会得到最大,意味着这两堆数据很相似很接近,他们之间的散度就是很小的。反之亦然。
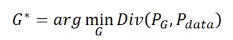
数学证明
为什么训练目标函数和散度有关呢?
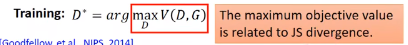
下面证明:
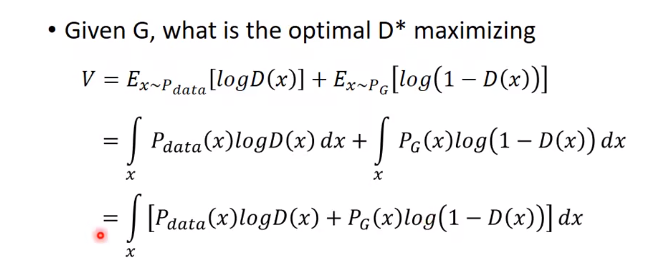
假设:D(x)可以是任何函数
上式相当于,找到一个D,让积分里面的部分最大:
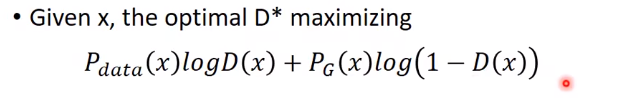
为了看起来方便,让Pdata = a, PG = b, D(x) = D。
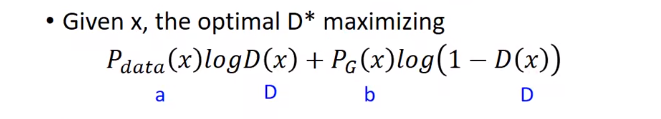
可得到如下,求导,让导数为0。就可得到D*
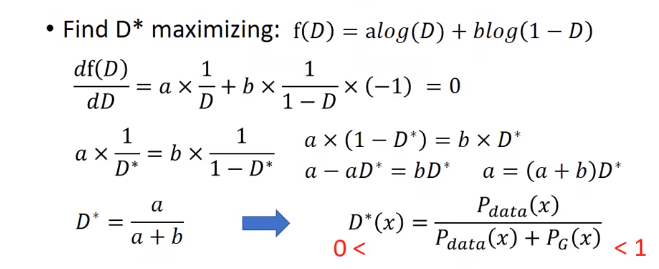
此时得到局部最大。
接下来,把刚才求得的D*代入目标函数:
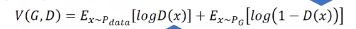
得到下式:

为了把它整理成像JS散度,就作一些变换,分子分母同除以2:
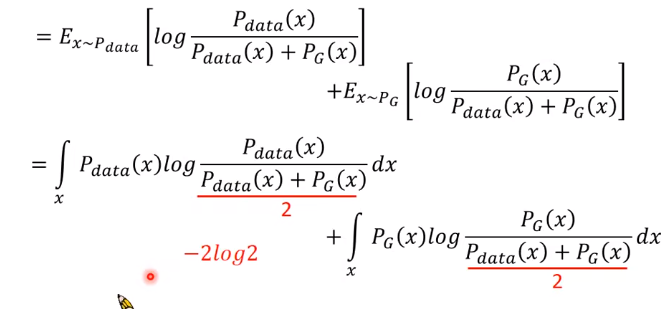
把分子的1/2都提出来,放到前面,就是2log(1/2),或 -2log2。
最后式子可以写成如下:

回顾一下JS散度的公式:
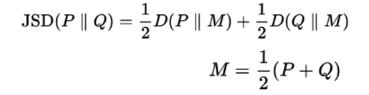
所以可以看到,最后最大化目标函数就是在最大化它们的JS散度。