目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
5.算法完整程序工程
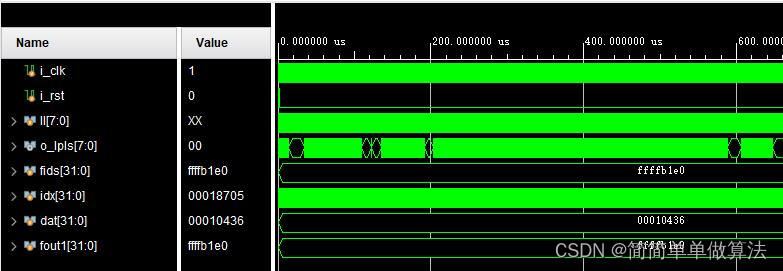
1.算法运行效果图预览

2.算法运行软件版本
matlab2022a
vivado2019.2
3.部分核心程序
`timescale 1ns / 1ps
//
// Company:
// Engineer:
//
// Create Date: 2022/07/28 01:51:45
// Design Name:
// Module Name: test_image
// Project Name:
// Target Devices:
// Tool Versions:
// Description:
//
// Dependencies:
//
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
//
//module test_image;reg i_clk;
reg i_rst;
reg [7:0] Buffer [0:100000];
reg [7:0] II;
wire [7:0] o_lpls;
integer fids,idx=0,dat;//D:\FPGA_Proj\FPGAtest\codepz\project_1\project_1.srcs\sources_1
initial
beginfids = $fopen("D:\\FPGA_Proj\\FPGAtest\\codepz\\test0.bmp","rb");dat = $fread(Buffer,fids);$fclose(fids);
endinitial
begin
i_clk=1;
i_rst=1;
#1000;
i_rst=0;
end always #5 i_clk=~i_clk;always@(posedge i_clk)
beginII<=Buffer[idx];idx<=idx+1;
endtops tops_u(
.i_clk (i_clk),
.i_rst (i_rst),
.i_I (II),
.o_lpls (o_lpls)
);integer fout1;
initial beginfout1 = $fopen("SAVEDATA.txt","w");
endalways @ (posedge i_clk)begin$fwrite(fout1,"%d\n",o_lpls);endendmodule
0X_018m4.算法理论概述
拉普拉斯变换是一种二阶微分算子,用于图像增强和边缘检测。它通过计算图像中每个像素点周围像素的灰度差值,突出图像中的高频成分,从而增强边缘和细节。
对于二维图像f(x,y),拉普拉斯变换定义为:
∇²f = ∂²f/∂x² + ∂²f/∂y²
在实际应用中,常用离散化的拉普拉斯算子来计算图像的拉普拉斯变换。常见的离散化拉普拉斯算子有4邻域和8邻域两种,分别对应以下模板:
4邻域模板:
0 -1 0
-1 4 -1
0 -1 0
8邻域模板:
-1 -1 -1
-1 8 -1
-1 -1 -1
基于FPGA的图像拉普拉斯变换实现需要将上述数学公式转化为硬件电路,通过编程实现对图像的实时处理。具体步骤如下:
- 图像输入:将待处理的图像数据输入到FPGA中,可以通过摄像头、图像传感器等设备获取。
- 缓存图像:在FPGA中缓存输入的图像数据,以便后续处理。
- 拉普拉斯变换:根据选择的离散化拉普拉斯算子,设计相应的硬件电路,对每个像素点进行拉普拉斯变换计算。
- 输出结果:将计算得到的拉普拉斯变换结果输出到显示器或其他输出设备中,完成图像处理。
在实现过程中,需要注意以下几点:
- 硬件资源:根据处理速度和图像大小的要求,选择合适的FPGA型号和硬件配置,确保资源足够且性能满足需求。
- 算法优化:针对具体的应用场景和硬件资源,对拉普拉斯变换算法进行优化,提高处理速度和精度。
- 编程语言:选择适合的硬件描述语言(如Verilog、VHDL等)进行编程,实现硬件电路的功能。
基于FPGA的图像拉普拉斯变换实现需要结合数字图像处理、硬件设计和编程等多个领域的知识,通过合理的算法设计和硬件优化,实现对图像的实时处理和增强。