P7473 重力球

Solution

考虑 Brute Force：对于每一次询问，通过 BFS 处理出最近的交汇点，输出答案。

很显然，会 $TLE$。

故，考虑 优化：

观察发现障碍物数量非常少，故设状态 $(\mathrm{x},\mathrm{y},\mathrm{d})$ 表示第 $1$ 个小球被第 $x$ 个障碍物卡住，第 $2$ 个小球被第 $y$ 个小球卡住，在障碍物的 $d$ 方向（如图）。此时，发现总共的状态数量不多。

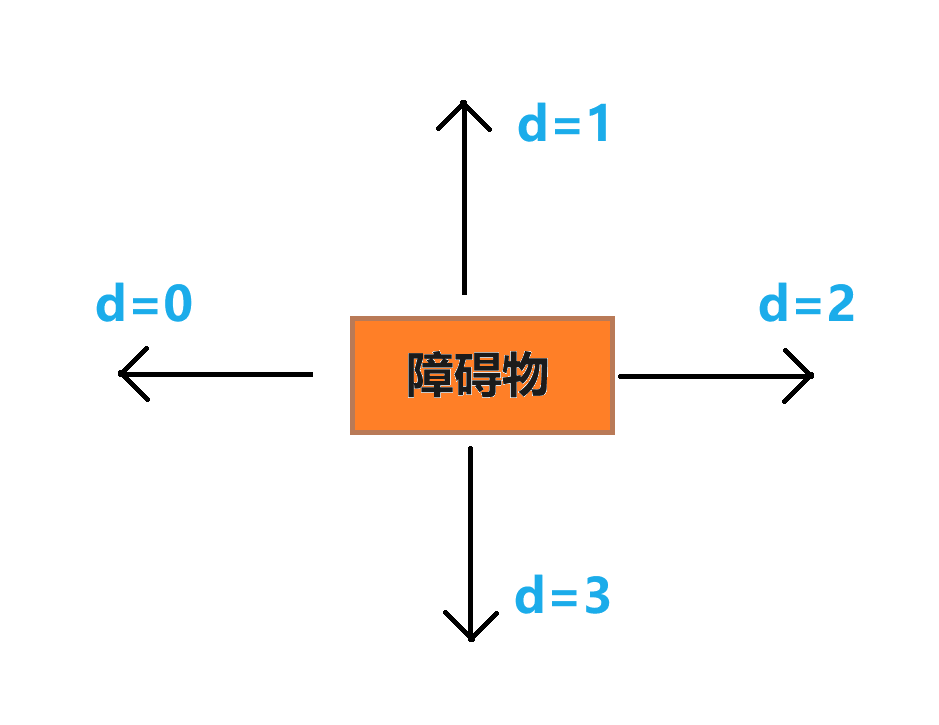
这样我们就可以用着 $3$ 个数来确定出每个小球的位置。

之后，考虑每一次走一定是走到一个 障碍物四周 的点，所以可以提前预处理，记作 $\mathrm{T}{\mathrm{o}}_{\mathrm{i},\mathrm{j},\mathrm{k}}$ 表示 $(i,j)$ 向 $k$ 方向会走到的点。

对于任意两个起点，需要向四周可到达的点连边：

假设当前是 ${\mathrm{x}}_1,{\mathrm{y}}_1,\mathrm{d}$，方向是 $2$，那么运动之后，$\mathrm{d}=\mathrm{d}\oplus 2$（即原来在上面，变成下面；原来在左边，变成右边…… 通过上图观察发现异或 $2$ 可以解决）；点会变为 $\mathrm{T}{\mathrm{o}}_{{\mathrm{x}}_1,{\mathrm{y}}_1,2}$

依此建边即可。

---

预处理操作结束之后，对于每一个询问：

1. 直接 BFS 算出终点为哪个点最近（易 $\mathrm{TLE}$）
2. 正难则反，考虑对于所有可能终点中到这两个点的最短距离，这其实就是一个 多源BFS！注意：使用该方法需建反边！

建议采取第 $2$ 种操作，当然这样并不需要每一次都进行 BFS，只需提前做 $1$ 次即可。

由于，每一次询问的时候，不一定是在一个 障碍物四周，所以需要上、下、左、右四个方向，跑到障碍物四周，然后取最小值即可。

---

Code

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>using namespace std;typedef pair<int, int> PII;
typedef long long LL;const int SIZE = 255;int N, M, Q;
vector<PII> Obstackle;
int Is[SIZE][SIZE], Id[SIZE][SIZE], cnt;
int dx[4] = {0, -1, 0, 1}, dy[4] = {-1, 0, 1, 0};
int To[SIZE][SIZE][4], Dist[SIZE * 5][SIZE * 5][4];
struct P
{int x, y, d;
};
std::vector<P> G[SIZE * 5][SIZE * 5][4];
int Vis[SIZE * 5][SIZE * 5][4];bool check(int x, int y)
{return x >= 1 && y >= 1 && x <= N && y <= N && !Is[x][y];
}void Init()
{for (int i = 1; i <= N; i ++)for (int j = 1; j <= N; j ++)for (int k = 0; k < 4; k ++){int x = i, y = j;while (!Is[x][y])x += dx[k], y += dy[k];To[i][j][k] = Id[x][y];}for (auto i : Obstackle)for (auto j : Obstackle)for (int sd = 0; sd < 4; sd ++)for (int k = 0; k < 4; k ++){int x1 = i.first + dx[k], y1 = i.second + dy[k], x2 = j.first + dx[k], y2 = j.second + dy[k];if (check(x1, y1) && check(x2, y2)){int To1 = To[x1][y1][sd], To2 = To[x2][y2][sd];G[To1][To2][sd ^ 2].push_back({Id[i.first][i.second], Id[j.first][j.second], k});}}
}void BFS()
{memset(Dist, 0x3f, sizeof Dist);queue<P> Q;for (auto c : Obstackle)for (int i = 0; i < 4; i ++){int id = Id[c.first][c.second];int x = c.first + dx[i], y = c.second + dy[i];if (check(x, y))Dist[id][id][i] = 0, Q.push({id, id, i});}while (Q.size()){auto Tmp = Q.front();Q.pop();if (Vis[Tmp.x][Tmp.y][Tmp.d]) continue;Vis[Tmp.x][Tmp.y][Tmp.d] = 1;for (auto c : G[Tmp.x][Tmp.y][Tmp.d])if (Dist[c.x][c.y][c.d] > Dist[Tmp.x][Tmp.y][Tmp.d] + 1){Q.push(c);Dist[c.x][c.y][c.d] = min(Dist[c.x][c.y][c.d], Dist[Tmp.x][Tmp.y][Tmp.d] + 1);}}
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> N >> M >> Q;for (int i = 1; i <= M; i ++){int x, y;cin >> x >> y;Id[x][y] = ++ cnt;Is[x][y] = 1;Obstackle.push_back({x, y});}for (int i = 0; i <= N + 1; i ++)for (int j = 0; j <= N + 1; j ++)if (!i || !j || i > N || j > N){Id[i][j] = ++ cnt;Is[i][j] = 1;Obstackle.push_back({i, j});}Init();BFS();while (Q --){int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;int Result = 2e9;for (int i = 0; i < 4; i ++)Result = min(Result, Dist[To[x1][y1][i]][To[x2][y2][i]][i ^ 2] + 1);if (x1 == x2 && y1 == y2) Result = 0;if (Result >= 1e9) Result = -1;cout << Result << endl;}return 0;
}