一文通透位置编码：从标准位置编码到旋转位置编码RoPE-编程知识

前言

关于位置编码和RoPE

我之前在本博客中的另外两篇文章中有阐述过(一篇是关于LLaMA解读的，一篇是关于transformer从零实现的)，但自觉写的不是特别透彻好懂
再后来在我参与主讲的类ChatGPT微调实战课中也有讲过，但有些学员依然反馈RoPE不是特别好理解

为彻底解决这个位置编码/RoPE的问题，我把另外两篇文章中关于这部分的内容抽取出来，并不断深入、扩展、深入，最终成为本文

第一部分 transformer原始论文中的标准位置编码

如此篇文章《Transformer通俗笔记：从Word2Vec、Seq2Seq逐步理解到GPT、BERT》所述，RNN的结构包含了序列的时序信息，而Transformer却完全把时序信息给丢掉了，比如“他欠我100万”，和“我欠他100万”，两者的意思千差万别，故为了解决时序的问题，Transformer的作者用了一个绝妙的办法：位置编码(Positional Encoding)

1.1 标准位置编码的起源

即将每个位置编号，从而每个编号对应一个向量，最终通过结合位置向量和词向量，作为输入embedding，就给每个词都引入了一定的位置信息，这样Attention就可以分辨出不同位置的词了，具体怎么做呢？

如果简单粗暴的话，直接给每个向量分配一个数字，比如1到1000之间
也可以用one-hot编码表示位置
transformer论文中作者通过sin函数和cos函数交替来创建 positional encoding，其计算positional encoding的公式如下
$PE_{(pos,2i+1)} = cos\left ( \frac{pos}{10000^{\frac{2i}{d_{model}}}} \right )$

$PE_{(pos,2i)} = sin\left ( \frac{pos}{10000^{\frac{2i}{d_{model}}}} \right )$
其中，pos相当于是每个token在整个序列中的位置，相当于是0, 1, 2, 3...(看序列长度是多大，比如10，比如100)， $d_{model}$ 代表位置向量的维度(也是词embedding的维度，transformer论文中设置的512维)
至于 $i$ 是embedding向量的位置下标对2求商并取整(可用双斜杠 $//$ 表示整数除法，即求商并取整)，它的取值范围是 $[0,...,\frac{d_{model}}{2}]$ ，比如
$i = 0 // 2 = 0$ ， $2i = 0$
$i = 1 //2 =0$ ， $2i = 0,2i+1 = 1$
$i = 2 // 2 = 1$ ， $2i = 2$
$i = 3 // 2 = 1$ ， $2i = 2,2i+1 = 3$
$i = 4 // 2 = 2$ ， $2i = 4$
$i = 5//2 = 2$ ， $2i = 4, 2i + 1 =5$
...
$i = 510 // 2 = 255$ ， $2i = 510$
$i = 511 // 2 = 255$ ， $2i = 510,2i + 1 = 511$
相当于
$2i$ 是指向量维度中的偶数维，即第0维、第2维、第4维...，第510维，用sin函数计算
$2i+1$ 是向量维度中的奇数维，即第1维、第3维、第5维..，第511维，用cos函数计算

不要小看transformer的这个位置编码，不少做NLP多年的人也不一定对其中的细节有多深入，而网上大部分文章谈到这个位置编码时基本都是千篇一律、泛泛而谈，很少有深入，故本文还是细致探讨下

1.2 标准位置编码的示例：多图多举例

考虑到一图胜千言一例胜万语，举个例子，当我们要编码「我爱你」的位置向量，假定每个token都具备512维，如果位置下标从0开始时，则根据位置编码的计算公式可得『且为让每个读者阅读本文时一目了然，我计算了每个单词对应的位置编码示例(在此之前，这些示例在其他地方基本没有)』

当对 $pos = 0$ 上的单词「我」进行位置编码时，它本身的维度有512维
$PE_0 = [sin(\frac{0}{10000^{\frac{0}{512}}}),cos(\frac{0}{10000^{\frac{0}{512}}}), sin(\frac{0}{10000^{\frac{2}{512}}}),cos(\frac{0}{10000^{\frac{2}{512}}}), sin(\frac{0}{10000^{\frac{4}{512}}}), cos(\frac{0}{10000^{\frac{4}{512}}}),..., sin(\frac{0}{10000^{\frac{510}{512}}}),cos(\frac{0}{10000^{\frac{510}{512}}})]$
当对 $pos = 1$ 上的单词「爱」进行位置编码时，它本身的维度有512维
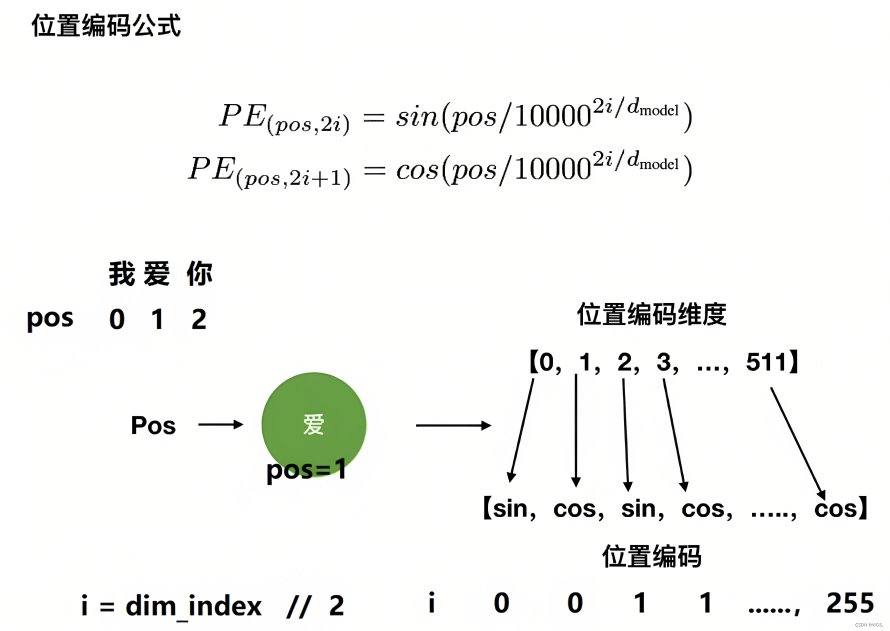
$PE_1 = [sin(\frac{1}{10000^{\frac{0}{512}}}),cos(\frac{1}{10000^{\frac{0}{512}}}), sin(\frac{1}{10000^{\frac{2}{512}}}),cos(\frac{1}{10000^{\frac{2}{512}}}), sin(\frac{1}{10000^{\frac{4}{512}}}), cos(\frac{1}{10000^{\frac{4}{512}}}),..., sin(\frac{1}{10000^{\frac{510}{512}}}),cos(\frac{1}{10000^{\frac{510}{512}}})]$
然后再叠加上embedding向量，可得
当对 $pos = 2$ 上的单词「你」进行位置编码时，它本身的维度有512维
$PE_2 = [sin(\frac{2}{10000^{\frac{0}{512}}}),cos(\frac{2}{10000^{\frac{0}{512}}}), sin(\frac{2}{10000^{\frac{2}{512}}}),cos(\frac{2}{10000^{\frac{2}{512}}}), sin(\frac{2}{10000^{\frac{4}{512}}}), cos(\frac{2}{10000^{\frac{4}{512}}}),..., sin(\frac{2}{10000^{\frac{510}{512}}}),cos(\frac{2}{10000^{\frac{510}{512}}})]$
....

最终得到的可视化效果如下图所示

1.3 标准位置编码的coding实现

代码实现如下

“”“位置编码的实现，调用父类nn.Module的构造函数”“”
class PositionalEncoding(nn.Module):def __init__(self, d_model, dropout, max_len=5000):super(PositionalEncoding, self).__init__()  self.dropout = nn.Dropout(p=dropout)  # 初始化dropout层# 计算位置编码并将其存储在pe张量中pe = torch.zeros(max_len, d_model)                # 创建一个max_len x d_model的全零张量position = torch.arange(0, max_len).unsqueeze(1)  # 生成0到max_len-1的整数序列，并添加一个维度# 计算div_term，用于缩放不同位置的正弦和余弦函数div_term = torch.exp(torch.arange(0, d_model, 2) *-(math.log(10000.0) / d_model))# 使用正弦和余弦函数生成位置编码，对于d_model的偶数索引，使用正弦函数；对于奇数索引，使用余弦函数。pe[:, 0::2] = torch.sin(position * div_term)pe[:, 1::2] = torch.cos(position * div_term)pe = pe.unsqueeze(0)                  # 在第一个维度添加一个维度，以便进行批处理self.register_buffer('pe', pe)        # 将位置编码张量注册为缓冲区，以便在不同设备之间传输模型时保持其状态# 定义前向传播函数def forward(self, x):# 将输入x与对应的位置编码相加x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)# 应用dropout层并返回结果return self.dropout(x)

本文发布之后，有同学留言问，上面中的第11行、12行代码

div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))

为什么先转换为了等价的指数+对数运算，而不是直接幂运算？是效率、精度方面有差异吗？

这里使用指数和对数运算的原因是为了确保数值稳定性和计算效率。

一方面，直接使用幂运算可能会导致数值上溢或下溢。当d_model较大时，10000.0 ** (-i / d_model)中的幂可能会变得非常小，以至于在数值计算中产生下溢。通过将其转换为指数和对数运算，可以避免这种情况，因为这样可以在计算过程中保持更好的数值范围
二方面，在许多计算设备和库中，指数和对数运算的实现通常比幂运算更快。这主要是因为指数和对数运算在底层硬件和软件中有特定的优化实现，而幂运算通常需要计算更多的中间值

所以，使用指数和对数运算可以在保持数值稳定性的同时提高计算效率。

既然提到了这行代码，我们干脆就再讲更细致些，上面那行代码对应的公式为

其中的中括号对应的是一个从 0 到 $d_{\text{model}} - 1$ 的等差数列(步长为 2)，设为 $i$

且上述公式与这个公式是等价的

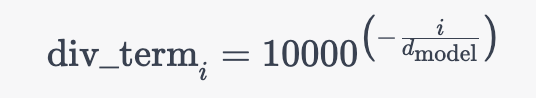
为何，原因在于 $a^x=e^{(x\cdot ln(a))}$ ，从而有 $10000^{-\frac{i}{d_{model}}}=e^{(-\frac{i}{d_{model}}\cdot log(10000))}$

最终，再通过下面这两行代码完美实现位置编码

        # 使用正弦和余弦函数生成位置编码，对于d_model的偶数索引，使用正弦函数；对于奇数索引，使用余弦函数。pe[:, 0::2] = torch.sin(position * div_term)pe[:, 1::2] = torch.cos(position * div_term)

第二部分如何彻底理解旋转位置嵌入(RoPE)

在位置编码上，删除了绝对位置嵌入，而在网络的每一层增加了苏剑林等人(2021)提出的旋转位置嵌入(RoPE)，其思想是采用绝对位置编码的形式实现相对位置编码，且RoPE主要借助了复数的思想

先复习下复数的一些关键概念

我们一般用 $a + bi$ 表示复数，实数a叫做复数的实部，实数b叫做复数的虚部
复数的辐角是指复数在复平面上对应的向量和正向实数轴所成的有向角

$z = a + ib$ 的共轭复数定义为： $z^* = a - ib$ ，也可记作 $\bar{z}$ ，复数与其共轭的乘积等于它的模的平方，即 $z \times z^* = a^2 + b^2 = |z|^2$ ，这是一个实数
当 $x$ 表示任意实数， $e$ 是自然对数的底数， $i$ 是复数中的虚数单位，则根据欧拉公式有
$e^{i x}=\cos x+i \sin x$
表达的含义在于该指数函数可以表示为实部为 $cos x$ ，虚部为 $sinx$ 的一个复数
该欧拉公式相当于建立了指数函数、三角函数和复数之间的桥梁

2.1 旋转位置编码的原理与推导

当咱们给self-attention中的 $q,k,v$ 向量都加入了位置信息后，便可以表示为

$\begin{aligned} \boldsymbol{q}_{m} & =f_{q}\left(\boldsymbol{x}_{m}, m\right) \\ \boldsymbol{k}_{n} & =f_{k}\left(\boldsymbol{x}_{n}, n\right) \\ \boldsymbol{v}_{n} & =f_{v}\left(\boldsymbol{x}_{n}, n\right) \end{aligned}$

其中

$\boldsymbol{q}_{m}$ 表示第 $m$ 个 token 对应的词向量 $x_m$ 集成位置信息 $m$ 之后的 query 向量
而 $k_n$ 和 $v_n$ 则表示第 $n$ 个 token 对应的词向量 $x_n$ 集成位置信息 $n$ 之后的 key 和 value 向量

2.1.1 第一种形式的推导(通俗易懂版)

接着论文中提出为了能利用上 token 之间的相对位置信息，假定 query 向量 $q_m$ 和 key 向量 $k_n$ 之间的内积操作可以被一个函数 $g$ 表示，该函数 $g$ 的输入是词嵌入向量 $x_m$ 、 $x_n$ ，它们之间的相对位置 $m - n$ ：

$<f_{q}\left(x_{m}, m\right), f_{k}\left(x_{n}, n\right)>=g\left(x_{m}, x_{n}, m-n\right)$

假定现在词嵌入向量的维度是两维 $d = 2$ ，这样就可以利用上2维度平面上的向量的几何性质，然后论文中提出了一个满足上述关系的 $f$ 和 $g$ 的形式如下：

$\begin{array}{l} f_{q}\left(\boldsymbol{x}_{m}, m\right)=\left(\boldsymbol{W}_{q} \boldsymbol{x}_{m}\right) e^{i m \theta} \\ f_{k}\left(\boldsymbol{x}_{n}, n\right)=\left(\boldsymbol{W}_{k} \boldsymbol{x}_{n}\right) e^{i n \theta} \\ g\left(\boldsymbol{x}_{m}, \boldsymbol{x}_{n}, m-n\right)=\operatorname{Re}\left[\left(\boldsymbol{W}_{q} \boldsymbol{x}_{m}\right)\left(\boldsymbol{W}_{k} \boldsymbol{x}_{n}\right)^{*} e^{i(m-n) \theta}\right] \end{array}$

这里面 Re 表示复数的实部

进一步地， $f_q$ 可以表示成下面的式子：

$\begin{aligned} f_{q}\left(\boldsymbol{x}_{m}, m\right) & =\left(\begin{array}{cc} \cos m \theta & -\sin m \theta) \\ \sin m \theta & \cos m \theta \end{array}\right)\left(\begin{array}{ll} W_{q}^{(1,1)} & W_{q}^{(1,2)} \\ W_{q}^{(2,1)} & W_{q}^{(2,2)} \end{array}\right)\left(\begin{array}{c} x_{m}^{(1)} \\ x_{m}^{(2)} \end{array}\right) \\ & =\left(\begin{array}{cc} \cos m \theta & -\sin m \theta) \\ \sin m \theta & \cos m \theta \end{array}\right)\left(\begin{array}{c} q_{m}^{(1)} \\ q_{m}^{(2)} \end{array}\right) \end{aligned}$

看到这里会发现，这不就是 query 向量乘以了一个旋转矩阵吗？这就是为什么叫做旋转位置编码的原因

同理， $f_k$ 可以表示成下面的式子：

$\begin{aligned} f_{k}\left(\boldsymbol{x}_{m}, m\right) & =\left(\begin{array}{cc} \cos m \theta & -\sin m \theta) \\ \sin m \theta & \cos m \theta \end{array}\right)\left(\begin{array}{ll} W_{k}^{(1,1)} & W_{k}^{(1,2)} \\ W_{k}^{(2,1)} & W_{k}^{(2,2)} \end{array}\right)\left(\begin{array}{c} x_{m}^{(1)} \\ x_{m}^{(2)} \end{array}\right) \\ & =\left(\begin{array}{cc} \cos m \theta & -\sin m \theta) \\ \sin m \theta & \cos m \theta \end{array}\right)\left(\begin{array}{l} k_{m}^{(1)} \\ k_{m}^{(2)} \end{array}\right) \end{aligned}$

最终 $g\left(\boldsymbol{x}_{m}, \boldsymbol{x}_{n}, m-n\right)$ 可以表示如下：

$g\left(\boldsymbol{x}_{m}, \boldsymbol{x}_{n}, m-n\right)=\left(\begin{array}{ll} \boldsymbol{q}_{m}^{(1)} & \boldsymbol{q}_{m}^{(2)} \end{array}\right)\left(\begin{array}{cc} \cos ((m-n) \theta) & -\sin ((m-n) \theta) \\ \sin ((m-n) \theta) & \cos ((m-n) \theta) \end{array}\right)\left(\begin{array}{c} k_{n}^{(1)} \\ k_{n}^{(2)} \end{array}\right)$

然上述分别关于 $f_q$ 、 $f_k$ 、 $g\left(\boldsymbol{x}_{m}, \boldsymbol{x}_{n}, m-n\right)$ 的三个式子，咋一步一步推导来的？为做细致说明，特参考此文一步一步解释下

根据欧拉公式 $e^{i x}=\cos x+i \sin x$ ，可得
$\begin{array}{c} e^{i m \theta}=\cos (m \theta)+i \sin (m \theta) \\ e^{i n \theta}=\cos (n \theta)+i \sin (n \theta) \\ e^{i(m-n) \theta}=\cos ((m-n) \theta)+i \sin ((m-n) \theta) \end{array}$
对于 $f_{q}\left(x_{m}, m\right)=\left(W_{q} x_{m}\right) e^{i m \theta}$
可知其中的 $W_q$ 是个二维矩阵， $x_m$ 是个二维向量，自然相乘的结果也必然是一个二维向量，用 $q_m$ 表示
$q_{m}=\left(\begin{array}{c} q_{m}^{(1)} \\ q_{m}^{(2)} \end{array}\right)=W_{q} x_{m}=\left(\begin{array}{ll} W_{q}^{(11)} & W_{q}^{(12)} \\ W_{q}^{(21)} & W_{q}^{(22)} \end{array}\right)\left(\begin{array}{c} x_{m}^{(1)} \\ x_{m}^{(2)} \end{array}\right)$
然后将 $q_m$ 表示成复数形式，可得
$q_{m}=\left[q_{m}^{(1)}, q_{m}^{(2)}\right]=\left[q_{m}^{(1)}+i q_{m}^{(2)}\right]$
所以对于 $f_{q}\left(x_{m}, m\right)=\left(W_{q} x_{m}\right) e^{i m \theta}=q_{m} e^{i m \theta}$
即是两个复数相乘
$q_{m} e^{i m \theta}=\left(q_{m}^{(1)}+i q_{m}^{(2)}\right) *(\cos (m \theta)+i \sin (m \theta))$
考虑到以下两个关于复数的背景知识
$(a+i b) \cdot(c+i d)=a c+i b c+i a d+i^{2} b d=(a c-b d)+i(b c+a d)$
$i^{2}=-1$

可得
$\begin{aligned} q_{m} e^{i m \theta} & =\left(q_{m}^{(1)}+i q_{m}^{(2)}\right) *(\cos (m \theta)+i \sin (m \theta)) \\ =\left(q_{m}^{(1)} \cos (m \theta)\right. & \left.-q_{m}^{(2)} \sin (m \theta)\right)+i\left(q_{m}^{(2)} \cos (m \theta)+q_{m}^{(1)} \sin (m \theta)\right) \end{aligned}$

将这个结果表达成实数向量形式，即是
$q_{m} e^{i m \theta}=\left[q_{m}^{(1)} \cos (m \theta)-q_{m}^{(2)} \sin (m \theta), q_{m}^{(2)} \cos (m \theta)+q_{m}^{(1)} \sin (m \theta)\right]$

至此，你也就不难发现，这不就是query向量乘以了一个旋转矩阵么
$\begin{array}{c} f_{q}\left(x_{m}, m\right)=\left(W_{q} x_{m}\right) e^{i m \theta}=q_{m} e^{i m \theta} \\ =\left[q_{m}^{(1)} \cos (m \theta)-q_{m}^{(2)} \sin (m \theta), q_{m}^{(2)} \cos (m \theta)+q_{m}^{(1)} \sin (m \theta)\right] \\ =\left(\begin{array}{cc} \cos (m \theta) & -\sin (m \theta) \\ \sin (m \theta) & \cos (m \theta) \end{array}\right)\left(\begin{array}{c} q_{m}^{(1)} \\ q_{m}^{(2)} \end{array}\right) \end{array}$
同理，可得key向量 $k_n$
$\begin{array}{c} f_{k}\left(x_{n}, n\right)=\left(W_{k} x_{n}\right) e^{i n \theta}=k_{n} e^{i n \theta} \\ =\left[k_{n}^{(1)} \cos (n \theta)-k_{n}^{(2)} \sin (n \theta), k_{n}^{(2)} \cos (n \theta)+k_{n}^{(1)} \sin (n \theta)\right] \\ =\left(\begin{array}{cc} \cos (n \theta) & -\sin (n \theta) \\ \sin (n \theta) & \cos (n \theta) \end{array}\right)\left(\begin{array}{c} k_{n}^{(1)} \\ k_{n}^{(2)} \end{array}\right) \end{array}$
至于函数g，则可得
$g\left(x_{m}, x_{n}, m-n\right)=\operatorname{Re}\left[\left(W_{q} x_{m}\right)\left(W_{k} x_{n}\right)^{*} e^{i(m-n) \theta}\right]$
其中， $Re[x]$ 表示一个复数 $x$ 的实数部分，而 $\left(W_{k} x_{n}\right)^{*}$ 则表示复数 $W_{k} x_{n}$ 的共轭

考虑到
$\begin{array}{c} z=a+i b \\ z^{*}=a-i b \end{array}$
所以可得
$\begin{array}{c} W_{q} x_{m}=q_{m}=q_{m}^{(1)}+i q_{m}^{(2)} \\ W_{k} x_{n}=k_{n}=k_{n}^{(1)}+i k_{n}^{(2)} \\ \left(W_{k} x_{n}\right)^{*}=k_{n}^{*}=k_{n}^{(1)}-i k_{n}^{(2)} \\ e^{i(m-n) \theta}=\cos ((m-n) \theta)+i \sin ((m-n) \theta) \end{array}$

继续可得
$\begin{array}{c} g\left(x_{m}, x_{n}, m-n\right)=\operatorname{Re}\left[\left(W_{q} x_{m}\right)\left(W_{k} x_{n}\right)^{*} e^{i(m-n) \theta}\right] \\ =\operatorname{Re}\left[\left(q_{m}^{(1)}+i q_{m}^{(2)}\right)\left(k_{n}^{(1)}-i k_{n}^{(2)}\right)(\cos ((m-n) \theta)+i \sin ((m-n) \theta))\right] \\ =\operatorname{Re}\left[\left(\left(q_{m}^{(1)} k_{n}^{(1)}+q_{m}^{(2)} k_{n}^{(2)}\right)+i\left(q_{m}^{(2)} k_{n}^{(1)}-q_{m}^{(1)} k_{n}^{(2)}\right)\right)(\cos ((m-n) \theta)+i \sin ((m-n) \theta))\right] \\ =\left(q_{m}^{(1)} k_{n}^{(1)}+q_{m}^{(2)} k_{n}^{(2)}\right) \cos ((m-n) \theta)-\left(q_{m}^{(2)} k_{n}^{(1)}-q_{m}^{(1)} k_{n}^{(2)}\right) \sin ((m-n) \theta) \end{array}$
接下来我们就要证明函数 g 的计算公式是成立的
首先，回顾一下attention操作，位置m的query和位置n的key会做一个内积操作
即由
$\begin{array}{c} f_{q}\left(x_{m}, m\right)=\left[q_{m}^{(1)} \cos (m \theta)-q_{m}^{(2)} \sin (m \theta), q_{m}^{(2)} \cos (m \theta)+q_{m}^{(1)} \sin (m \theta)\right] \\ f_{k}\left(x_{n}, n\right)=\left[k_{n}^{(1)} \cos (n \theta)-k_{n}^{(2)} \sin (n \theta), k_{n}^{(2)} \cos (n \theta)+k_{n}^{(1)} \sin (n \theta)\right] \end{array}$
可得
$\begin{array}{c} <f_{q}\left(x_{m}, m\right), f_{k}\left(x_{n}, n\right)> \\ = \left(q_{m}^{(1)} \cos (m \theta)-q_{m}^{(2)} \sin (m \theta)\right)\left(k_{n}^{(1)} \cos (n \theta)-k_{n}^{(2)} \sin (n \theta)\right) \\ +\left(q_{m}^{(2)} \cos (m \theta)+q_{m}^{(1)} \sin (m \theta)\right)\left(k_{n}^{(2)} \cos (n \theta)+k_{n}^{(1)} \sin (n \theta)\right) \\ =q_{m}^{(1)} \cos (m \theta) k_{n}^{(1)} \cos (n \theta)-q_{m}^{(1)} \cos (m \theta) k_{n}^{(2)} \sin (n \theta) \\ -q_{m}^{(2)} \sin (m \theta) k_{n}^{(1)} \cos (n \theta)+q_{m}^{(2)} \sin (m \theta) k_{n}^{(2)} \sin (n \theta) \\ +q_{m}^{(2)} \cos (m \theta) k_{n}^{(2)} \cos (n \theta)+q_{m}^{(2)} \cos (m \theta) k_{n}^{(1)} \sin (n \theta) \\ +q_{m}^{(1)} \sin (m \theta) k_{n}^{(2)} \cos (n \theta)+q_{m}^{(1)} \sin (m \theta) k_{n}^{(1)} \sin (n \theta) \end{array}$
从而有
$\begin{array}{c} <f_{q}\left(x_{m}, m\right), f_{k}\left(x_{n}, n\right)>\\ = q_{m}^{(1)} k_{n}^{(1)}(\cos (m \theta) \cos (n \theta)+\sin (m \theta) \sin (n \theta)) \\ +q_{m}^{(1)} k_{n}^{(2)}(-\cos (m \theta) \sin (n \theta)+\sin (m \theta) \cos (n \theta)) \\ +q_{m}^{(2)} k_{n}^{(1)}(-\sin (m \theta) \cos (n \theta)+\cos (m \theta) \sin (n \theta)) \\ +q_{m}^{(2)} k_{n}^{(2)}(\sin (m \theta) \sin (n \theta)+\cos (m \theta) \cos (n \theta)) \\ =q_{m}^{(1)} k_{n}^{(1)} \cos ((m-n) \theta) \\ +q_{m}^{(1)} k_{n}^{(2)} \sin ((m-n) \theta) \\ -q_{m}^{(2)} k_{n}^{(1)} \sin ((m-n) \theta) \\ +q_{m}^{(2)} k_{n}^{(2)} \cos ((m-n) \theta) \\ =\left(q_{m}^{(1)} k_{n}^{(1)}+q_{m}^{(2)} k_{n}^{(2)}\right) \cos ((m-n) \theta)+\left(q_{m}^{(1)} k_{n}^{(2)}-q_{m}^{(2)} k_{n}^{(1)}\right) \sin ((m-n) \theta) \\ =\left(q_{m}^{(1)} k_{n}^{(1)}+q_{m}^{(2)} k_{n}^{(2)}\right) \cos ((m-n) \theta)-\left(q_{m}^{(2)} k_{n}^{(1)}-q_{m}^{(1)} k_{n}^{(2)}\right) \sin ((m-n) \theta) \\ =g\left(x_{m}, x_{n}, m-n\right) \end{array}$

咋来的？4个等式分4步
首先，把上述式子整理一下(把 $qk$ 相关的项提取出来)
其次，考虑到
$\begin{array}{l} \sin (a+b)=\sin a \cos b+\cos a \sin b \\ \sin (a-b)=\sin a \cos b-\cos a \sin b \\ \cos (a+b)=\cos a \cos b-\sin a \sin b \\ \cos (a-b)=\cos a \cos b+\sin a \sin b \end{array}$
最后两步，再把相关项调整下顺序即可

从而也就证明了，位置 m 的 query 和位置 n 的 key 的内积就是函数 g
把上面的式子用矩阵向量乘的形式来表达就是：
$\begin{array}{c} <f_{q}\left(x_{m}, m\right), f_{k}\left(x_{n}, n\right)> \\ =\left(\left(\begin{array}{cc} \cos (m \theta) & -\sin (m \theta) \\ \sin (m \theta) & \cos (m \theta) \end{array}\right)\left(\begin{array}{c} q_{m}^{(1)} \\ q_{m}^{(2)} \end{array}\right)\right)^{T}\left(\left(\begin{array}{cc} \cos (n \theta) & -\sin (n \theta) \\ \sin (n \theta) & \cos (n \theta) \end{array}\right)\left(\begin{array}{c} k_{n}^{(1)} \\ k_{n}^{(2)} \end{array}\right)\right) \\ =\left(\begin{array}{ll} q_{m}^{(1)} & q_{m}^{(2)} \end{array}\right)\left(\begin{array}{cc} \cos (m \theta) & \sin (m \theta) \\ -\sin (m \theta) & \cos (m \theta) \end{array}\right)\left(\begin{array}{cc} \cos (n \theta) & -\sin (n \theta) \\ \sin (n \theta) & \cos (n \theta) \end{array}\right)\left(\begin{array}{l} k_{n}^{(1)} \\ k_{n}^{(2)} \end{array}\right) \end{array}$

接下来，我们要计算两个旋转矩阵的乘积，即中间部分的这个式子
$\left(\begin{array}{cc} \cos (m \theta) & \sin (m \theta) \\ -\sin (m \theta) & \cos (m \theta) \end{array}\right)\left(\begin{array}{cc} \cos (n \theta) & -\sin (n \theta) \\ \sin (n \theta) & \cos (n \theta) \end{array}\right)$
展开之后，可得
$\left(\begin{array}{cc} \cos (m \theta) \cos (n \theta)+\sin (m \theta) \sin (n \theta) & -\cos (m \theta) \sin (n \theta)+\sin (m \theta) \cos (n \theta) \\ -\sin (m \theta) \cos (n \theta)+\cos (m \theta) \sin (n \theta) & \sin (m \theta) \sin (n \theta)+\cos (m \theta) \cos (n \theta) \end{array}\right)$

从而有
$\begin{array}{l} <f_{q}\left(x_{m}, m\right), {f_{k}\left(x_{n}, n\right)>} \\ =\left(\begin{array}{ll} q_{m}^{(1)} & q_{m}^{(2)} \end{array}\right)\left(\begin{array}{cc} \cos ((m-n) \theta) & -\sin ((m-n) \theta) \\ \sin ((m-n) \theta) & \cos ((m-n) \theta) \end{array}\right)\left(\begin{array}{c} k_{n}^{(1)} \\ k_{n}^{(2)} \end{array}\right) \end{array}$

上面都还只是针对词嵌入维度为2的情况，那对于 $d>=2$ 的通用情况呢，将2维推广到任意维度，可以表示如下：

$f_{\{q, k\}}\left(\boldsymbol{x}_{m}, m\right)=\boldsymbol{R}_{\Theta, m}^{d} \boldsymbol{W}_{\{q, k\}} \boldsymbol{x}_{m}$

内积满足线性叠加性，因此任意偶数维的RoPE，我们都可以表示为二维情形的拼接，即将词嵌入向量元素按照两两一组分组

$\boldsymbol{R}_{\Theta, m}^{d}=\underbrace{\left(\begin{array}{ccccccc} \cos m \theta_{0} & -\sin m \theta_{0} & 0 & 0 & \cdots & 0 & 0 \\ \sin m \theta_{0} & \cos m \theta_{0} & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m \theta_{1} & -\sin m \theta_{1} & \cdots & 0 & 0 \\ 0 & 0 & \sin m \theta_{1} & \cos m \theta_{1} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m \theta_{d / 2-1} & -\sin m \theta_{d / 2-1} \\ 0 & 0 & 0 & 0 & \cdots & \sin m \theta_{d / 2-1} & \cos m \theta_{d / 2-1} \end{array}\right)}_{\boldsymbol{W}_{m}}$

每组应用同样的旋转操作且每组的旋转角度计算方式如下：

$\Theta=\left\{\theta_{i}=10000^{-2(i-1) / d}, i \in[1,2, \ldots, d / 2]\right\}$

所以简单来说 RoPE 的 self-attention 操作的流程是

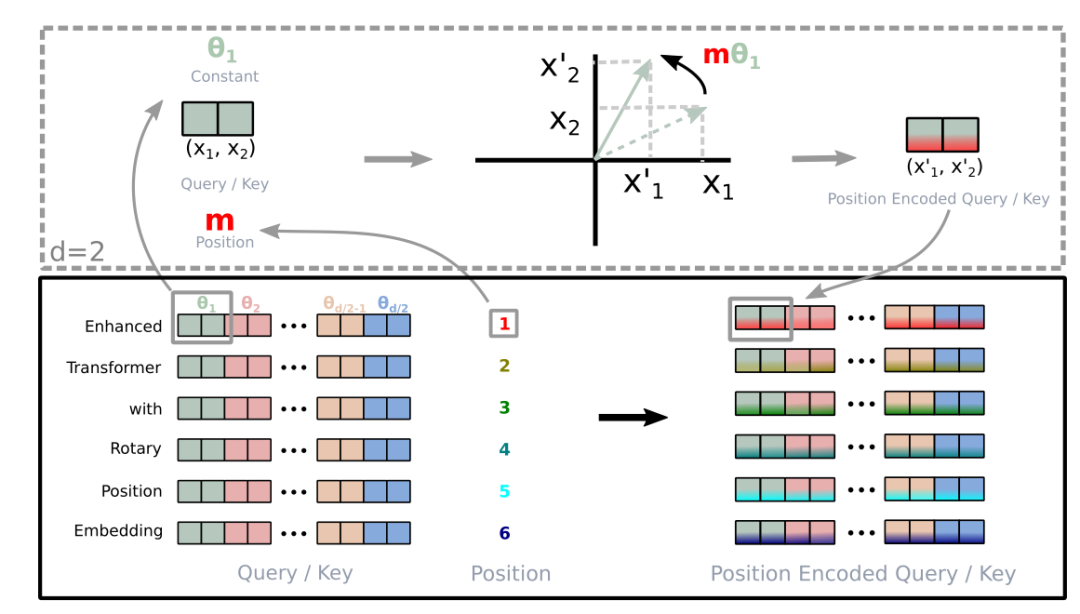
对于 token 序列中的每个词嵌入向量，首先计算其对应的 query 和 key 向量
然后对每个 token 位置都计算对应的旋转位置编码
接着对每个 token 位置的 query 和 key 向量的元素按照两两一组应用旋转变换
最后再计算 query 和 key 之间的内积得到 self-attention 的计算结果

2.1.2 第二种形式的推导(苏剑林版)

与上面第一种形式的推导类似，为了引入复数，首先假设了在加入位置信息之前，原有的编码向量是二维行向量 $q_m$ 和 $k_n$ ，其中 $m$ 和 $n$ 是绝对位置，现在需要构造一个变换，将 $m$ 和 $n$ 引入到 $q_m$ 和 $k_n$ 中，即寻找变换：

$\tilde {q_m} = f(q, m), \tilde{k_n} = f(k, n)$

也就是说，我们分别为 $q$ 、 $k$ 设计操作 $f(\cdot ,m)$ 、 $f(\cdot ,n)$ ，使得经过该操作后， $\tilde {q_m}$ 、 $\tilde{k_n}$ 就带有了位置 $m$ 、 $n$ 的绝对位置信息
考虑到Attention的核心计算是内积：

$Attention(Q, K,V) = softmax(\frac {QK^T} {\sqrt{d_k}})V$

故我们希望的内积的结果带有相对位置信息，即寻求的这个 $f(*)$ 变换，应该具有特性：

$\langle f(q, m), f(k, n) \rangle = g(q, k, m-n)$

「怎么理解？很简单，当m和n表示了绝对位置之后，m与n在句子中的距离即位置差m-n，就可以表示为相对位置了，且对于复数，内积通常定义为一个复数与另一个复数的共轭的乘积」

为合理的求出该恒等式的一个尽可能简单的解，可以设定一些初始条件，比如 $f(q,0)=q$ 、 $f(k,0)=k$ ，然后可以先考虑二维情形，然后借助复数来求解
在复数中有 $\langle\boldsymbol{q}, \boldsymbol{k}\rangle=\operatorname{Re}\left[\boldsymbol{q} \boldsymbol{k}^{*}\right]$ ， $Re[]$ 表示取实部的操作(复数 $q$ 和“ 复数 $k$ 的共轭即 $k^*$ ”之积仍是一个复数)，总之，我们需要寻找一种 $f(*)$ 变换，使得
$Re[f(q,m)f^{*}(k,n)] = g(q,k,m-n)$
简单起见，我们假设存在复数 $g(q,k,m-n)$ ，使得 $f(q,m)f^*(k,n)=g(q,k,m-n)$ ，然后我们用复数的指数形式，设
$\begin{aligned} \boldsymbol{f}(\boldsymbol{q}, m) & =R_{f}(\boldsymbol{q}, m) e^{\mathrm{i} \Theta_{f}(\boldsymbol{q}, m)} \\ \boldsymbol{f}(\boldsymbol{k}, n) & =R_{f}(\boldsymbol{k}, n) e^{\mathrm{i} \Theta_{f}(\boldsymbol{k}, n)} \\ \boldsymbol{g}(\boldsymbol{q}, \boldsymbol{k}, m-n) & =R_{g}(\boldsymbol{q}, \boldsymbol{k}, m-n) e^{\mathrm{i} \Theta_{g}(\boldsymbol{q}, \boldsymbol{k}, m-n)} \end{aligned}$
那么代入方程后就得到两个方程
方程1： $Rf(q,m)Rf(k,n) = Rg(q,k,m-n)$
方程2：Θf(q,m)−Θf(k,n) = Θg(q,k,m−n)

$\rightarrow$ 对于方程1，代入 $m=n$ 得到(接着，再把 $m$ 和 $n$ 都设为0)
$R_{f}(\boldsymbol{q}, m) R_{f}(\boldsymbol{k}, m)=R_{g}(\boldsymbol{q}, \boldsymbol{k}, 0)=R_{f}(\boldsymbol{q}, 0) R_{f}(\boldsymbol{k}, 0)=\|\boldsymbol{q}\|\|\boldsymbol{k}\|$
最后一个等号源于初始条件 $f(q,0) = q$ 和 $f(k,0) = k$ ，所以现在我们可以很简单地设 $Rf(q,m) = \left \| q \right \|$ ， $Rf(k,m)= \left \| k \right \|$ ，即它不依赖于 $m$

$\rightarrow$ 至于方程2，同样代入 $m=n$ 得到
Θf(q,m)−Θf(k,m) = Θg(q,k,0) = Θf(q,0)−Θf(k,0) = Θ(q)−Θ(k)

这里的 $\Theta(q)$ 、 $\Theta(k)$ 是 $q$ 、 $k$ 本身的幅角，而最后一个等号同样源于初始条件
根据上式Θf(q,m)−Θf(k,m) = Θ(q)−Θ(k)，可得Θf(q,m)−Θ(q)=Θf(k,m)−Θ(k)，所以Θf(q,m)−Θ(q)的结果是一个只与m相关、跟q无关的函数，记为φ(m)，即Θf(q,m)=Θ(q)+φ(m)
接着令n=m−1代入Θf(q,m)−Θf(k,n) = Θg(q,k,m−n)，可以得到 Θf(q,m)−Θf(k,m-1) = Θg(q,k,1)
然后将 Θf(q,m) 和 Θf(k,m-1) 的等式代入Θf(q,m)=Θ(q)+φ(m)，我们可以得到 Θ(q) + φ(m) - (Θ(k) + φ(m-1)) = Θg(q,k,1)，整理一下就得到
$\varphi(m)-\varphi(m-1)=\Theta g(q, k, 1)+\Theta(k)-\Theta(q)$
即{φ(m)}是等差数列，设右端为θ，那么就解得φ(m)=mθ

综上，我们得到二维情况下用复数表示的RoPE：
$\boldsymbol{f}(\boldsymbol{q}, m)=R_{f}(\boldsymbol{q}, m) e^{\mathrm{i} \Theta f(\boldsymbol{q}, m)}=\|q\| e^{\mathrm{i}(\Theta(\boldsymbol{q})+m \theta)}=\boldsymbol{q} e^{\mathrm{i} m \theta}$
所以说，寻求的变换就是 $q_me^{im\theta}$ ，也就是给 $q_m$ 乘以 $e^{im\theta}$ ，相应地， $k_n$ 乘以 $e^{in\theta}$
做了这样一个变换之后，根据复数的特性，有：
$\langle q_m, k_n \rangle = Re[q_mk^*_n]$
也就是，如果把二维向量看做复数，那么它们的内积，等于一个复数乘以另一个复数的共轭，得到的结果再取实部，代入上面的变换，也就有：
$\langle q_me^{im\theta}, k_ne^{in\theta} \rangle = Re[(q_me^{im\theta}) (k_ne^{in\theta})^*] =Re[q_mk_n^*e^{i(m-n)\theta}]$
这样一来，内积的结果就只依赖于 $(m-n)$ ，也就是相对位置了
换言之，经过这样一番操作，通过给Embedding添加绝对位置信息，可以使得两个token的编码，经过内积变换（self-attn）之后，得到结果是受它们位置的差值，即相对位置影响的

于是，对于任意的位置为 $m$ 的二维向量 $[x, y]$ ，把它看做复数，乘以 $e^{im\theta}$ ，而根据欧拉公式，有：

$e^{im\theta}=\cos{m\theta}+i\sin{m\theta}$

从而上述的相乘变换也就变成了(过程中注意： $i^2=-1$ )：

$(x+iy)e^{im\theta} \\= (x+ i y) (\cos{m\theta}+i\sin{m\theta}) \\= x\cos{m\theta} + ix\sin{m\theta} + iy\cos{m\theta} - y\sin{m\theta} \\ = (x\cos{m\theta}-y\sin{m\theta})+i(x\sin{m\theta}+y\cos{m\theta})$

把上述式子写成矩阵形式：

而这个变换的几何意义，就是在二维坐标系下，对向量 $(q_0, q_1)$ 进行了旋转，因而这种位置编码方法，被称为旋转位置编码

根据刚才的结论，结合内积的线性叠加性，可以将结论推广到高维的情形。可以理解为，每两个维度一组，进行了上述的“旋转”操作，然后再拼接在一起：

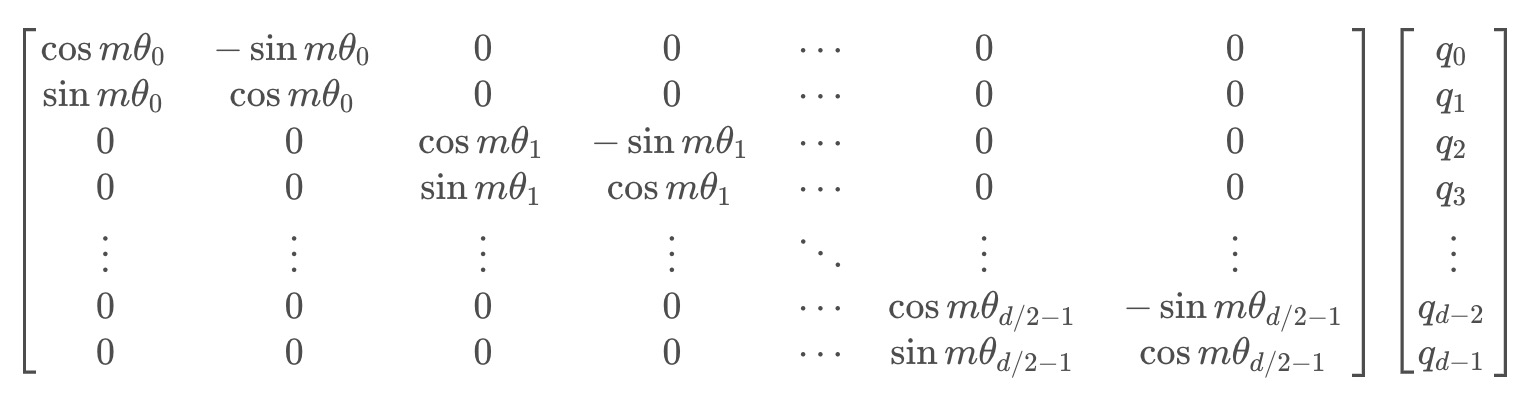
由于矩阵的稀疏性，会造成计算上的浪费，所以在计算时采用逐位相乘再相加的方式进行：

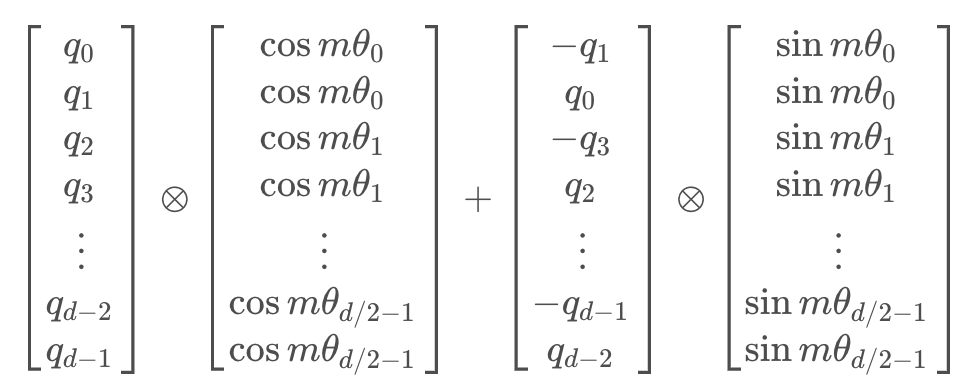
其中 $\otimes$ 为矩阵逐位相乘操作

更多可以参看此文：十分钟读懂旋转编码

2.2 旋转位置编码的coding实现(分非LLaMA版和LLaMA版两种)

原理理解了，接下来可以代码实现旋转位置编码，考虑到LLaMA本身的实现不是特别好理解，所以我们先通过一份非LLaMA实现的版本，最后再看下LLaMA实现的版本

对于，非LLaMA版的实现，其核心就是实现下面这三个函数 (再次强调，本份关于RoPE的非LLaMA版的实现与上面和之后的代码并非一体的，仅为方便理解RoPE的实现)

2.2.1 非LLaMA版的实现

2.2.1.1 sinusoidal_position_embedding的编码实现

sinusoidal_position_embedding：这个函数用来生成正弦形状的位置编码。这种编码用来在序列中的令牌中添加关于相对或绝对位置的信息

def sinusoidal_position_embedding(batch_size, nums_head, max_len, output_dim, device):# (max_len, 1)position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(-1)# (output_dim//2)# 即公式里的i, i的范围是 [0,d/2]ids = torch.arange(0, output_dim // 2, dtype=torch.float)  theta = torch.pow(10000, -2 * ids / output_dim)# (max_len, output_dim//2)# 即公式里的：pos / (10000^(2i/d))embeddings = position * theta # (max_len, output_dim//2, 2)embeddings = torch.stack([torch.sin(embeddings), torch.cos(embeddings)], dim=-1)# (bs, head, max_len, output_dim//2, 2)# 在bs维度重复，其他维度都是1不重复embeddings = embeddings.repeat((batch_size, nums_head, *([1] * len(embeddings.shape))))  # (bs, head, max_len, output_dim)# reshape后就是：偶数sin, 奇数cos了embeddings = torch.reshape(embeddings, (batch_size, nums_head, max_len, output_dim))embeddings = embeddings.to(device)return embeddings

一般的文章可能解释道这个程度基本就over了，但为了让初学者一目了然计，我还是再通过一个完整的示例，来一步步说明上述各个步骤都是怎么逐一结算的，整个过程和之前此文里介绍过的transformer的位置编码本质上是一回事..

为方便和transformer的位置编码做对比，故这里也假定output_dim = 512

首先，我们有 ids 张量，当 output_dim 为 512 时，则
$i = 0 // 2 = 0$ ， $2i = 0$
$i = 1 //2 =0$ ， $2i = 0,2i+1 = 1$
$i = 2 // 2 = 1$ ， $2i = 2$
$i = 3 // 2 = 1$ ， $2i = 2,2i+1 = 3$
$i = 4 // 2 = 2$ ， $2i = 4$
$i = 5//2 = 2$ ， $2i = 4, 2i + 1 =5$
...
$i = 510 // 2 = 255$ ， $2i = 510$
$i = 511 // 2 = 255$ ， $2i = 510,2i + 1 = 511$
ids = [0,0, 1,1, 2,2, ..., 254,254, 255,255]
然后我们有一个基数为10000的指数运算，使用了公式 torch.pow(10000, -2 * ids / output_dim)
$[\frac{1}{10000^{\frac{0}{512}}},\frac{1}{10000^{\frac{0}{512}}}, \frac{1}{10000^{\frac{2}{512}}},\frac{1}{10000^{\frac{2}{512}}}, \frac{1}{10000^{\frac{4}{512}}}, \frac{1}{10000^{\frac{4}{512}}},..., \frac{1}{10000^{\frac{510}{512}}},\frac{1}{10000^{\frac{510}{512}}}]$
执行 embeddings = position * theta 这行代码，它会将 position 的每个元素与 theta 的相应元素相乘，前三个元素为 $[\frac{0}{10000^{\frac{0}{512}}},\frac{0}{10000^{\frac{0}{512}}}, \frac{0}{10000^{\frac{2}{512}}},\frac{0}{10000^{\frac{2}{512}}}, \frac{0}{10000^{\frac{4}{512}}}, \frac{0}{10000^{\frac{4}{512}}},..., \frac{0}{10000^{\frac{510}{512}}},\frac{0}{10000^{\frac{510}{512}}}]$
$[\frac{1}{10000^{\frac{0}{512}}},\frac{1}{10000^{\frac{0}{512}}}, \frac{1}{10000^{\frac{2}{512}}},\frac{1}{10000^{\frac{2}{512}}}, \frac{1}{10000^{\frac{4}{512}}}, \frac{1}{10000^{\frac{4}{512}}},..., \frac{1}{10000^{\frac{510}{512}}},\frac{1}{10000^{\frac{510}{512}}}]$
$[\frac{2}{10000^{\frac{0}{512}}},\frac{2}{10000^{\frac{0}{512}}}, \frac{2}{10000^{\frac{2}{512}}},\frac{2}{10000^{\frac{2}{512}}}, \frac{2}{10000^{\frac{4}{512}}}, \frac{2}{10000^{\frac{4}{512}}},..., \frac{2}{10000^{\frac{510}{512}}},\frac{2}{10000^{\frac{510}{512}}}]$
接下来我们将对 embeddings 的每个元素应用 torch.sin 和 torch.cos 函数
对于 torch.sin(embeddings)，我们将取 embeddings 中的每个元素的正弦值：
$[sin(\frac{0}{10000^{\frac{0}{512}}}), sin(\frac{0}{10000^{\frac{2}{512}}}), sin(\frac{0}{10000^{\frac{4}{512}}}),..., sin(\frac{0}{10000^{\frac{510}{512}}})]$
$[sin(\frac{1}{10000^{\frac{0}{512}}}), sin(\frac{1}{10000^{\frac{2}{512}}}), sin(\frac{1}{10000^{\frac{4}{512}}}),..., sin(\frac{1}{10000^{\frac{510}{512}}})]$
$[sin(\frac{2}{10000^{\frac{0}{512}}}), sin(\frac{2}{10000^{\frac{2}{512}}}), sin(\frac{2}{10000^{\frac{4}{512}}}),..., sin(\frac{2}{10000^{\frac{510}{512}}})]$
对于 torch.cos(embeddings)，我们将取 embeddings 中的每个元素的余弦值：
$[cos(\frac{0}{10000^{\frac{0}{512}}}),cos(\frac{0}{10000^{\frac{2}{512}}}), cos(\frac{0}{10000^{\frac{4}{512}}}),..., ,cos(\frac{0}{10000^{\frac{510}{512}}})]$
$[cos(\frac{1}{10000^{\frac{0}{512}}}),cos(\frac{1}{10000^{\frac{2}{512}}}), cos(\frac{1}{10000^{\frac{4}{512}}}),..., ,cos(\frac{1}{10000^{\frac{510}{512}}})]$
$[cos(\frac{2}{10000^{\frac{0}{512}}}),cos(\frac{2}{10000^{\frac{2}{512}}}), cos(\frac{2}{10000^{\frac{4}{512}}}),..., ,cos(\frac{2}{10000^{\frac{510}{512}}})]$
最后，torch.stack([torch.sin(embeddings), torch.cos(embeddings)], dim=-1) 将这两个新的张量沿着一个新的维度堆叠起来，得到的 embeddings如下
$PE_0 = [sin(\frac{0}{10000^{\frac{0}{512}}}),cos(\frac{0}{10000^{\frac{0}{512}}}), sin(\frac{0}{10000^{\frac{2}{512}}}),cos(\frac{0}{10000^{\frac{2}{512}}}), sin(\frac{0}{10000^{\frac{4}{512}}}), cos(\frac{0}{10000^{\frac{4}{512}}}),..., sin(\frac{0}{10000^{\frac{510}{512}}}),cos(\frac{0}{10000^{\frac{510}{512}}})]$

$PE_1 = [sin(\frac{1}{10000^{\frac{0}{512}}}),cos(\frac{1}{10000^{\frac{0}{512}}}), sin(\frac{1}{10000^{\frac{2}{512}}}),cos(\frac{1}{10000^{\frac{2}{512}}}), sin(\frac{1}{10000^{\frac{4}{512}}}), cos(\frac{1}{10000^{\frac{4}{512}}}),..., sin(\frac{1}{10000^{\frac{510}{512}}}),cos(\frac{1}{10000^{\frac{510}{512}}})]$

$PE_2 = [sin(\frac{2}{10000^{\frac{0}{512}}}),cos(\frac{2}{10000^{\frac{0}{512}}}), sin(\frac{2}{10000^{\frac{2}{512}}}),cos(\frac{2}{10000^{\frac{2}{512}}}), sin(\frac{2}{10000^{\frac{4}{512}}}), cos(\frac{2}{10000^{\frac{4}{512}}}),..., sin(\frac{2}{10000^{\frac{510}{512}}}),cos(\frac{2}{10000^{\frac{510}{512}}})]$

最终，得到如下结果

[[[[sin(\frac{0}{10000^{\frac{0}{512}}}), cos(\frac{0}{10000^{\frac{0}{512}}}), sin(\frac{0}{10000^{\frac{2}{512}}}), cos(\frac{0}{10000^{\frac{2}{512}}}), ..., cos(\frac{0}{10000^{\frac{510}{512}}})],[sin(\frac{1}{10000^{\frac{0}{512}}}), cos(\frac{1}{10000^{\frac{0}{512}}}), sin(\frac{1}{10000^{\frac{2}{512}}}), cos(\frac{1}{10000^{\frac{2}{512}}}), ..., cos(\frac{1}{10000^{\frac{510}{512}}})],[sin(\frac{2}{10000^{\frac{0}{512}}}), cos(\frac{2}{10000^{\frac{0}{512}}}), sin(\frac{2}{10000^{\frac{2}{512}}}), cos(\frac{2}{10000^{\frac{2}{512}}}), ..., cos(\frac{2}{10000^{\frac{510}{512}}})]]]
]

2.2.2.2 RoPE的编码实现

RoPE：这个函数将相对位置编码（RoPE）应用到注意力机制中的查询和键上。这样，模型就可以根据相对位置关注不同的位置

import torch
import torch.nn as nn
import torch.nn.functional as F
import mathdef RoPE(q, k):# q,k: (bs, head, max_len, output_dim)batch_size = q.shape[0]nums_head = q.shape[1]max_len = q.shape[2]output_dim = q.shape[-1]# (bs, head, max_len, output_dim)pos_emb = sinusoidal_position_embedding(batch_size, nums_head, max_len, output_dim, q.device)# cos_pos,sin_pos: (bs, head, max_len, output_dim)# 看rope公式可知，相邻cos，sin之间是相同的，所以复制一遍。如(1,2,3)变成(1,1,2,2,3,3)cos_pos = pos_emb[...,  1::2].repeat_interleave(2, dim=-1)  # 将奇数列信息抽取出来也就是cos 拿出来并复制sin_pos = pos_emb[..., ::2].repeat_interleave(2, dim=-1)  # 将偶数列信息抽取出来也就是sin 拿出来并复制# q,k: (bs, head, max_len, output_dim)q2 = torch.stack([-q[..., 1::2], q[..., ::2]], dim=-1)q2 = q2.reshape(q.shape)  # reshape后就是正负交替了# 更新qw, *对应位置相乘q = q * cos_pos + q2 * sin_posk2 = torch.stack([-k[..., 1::2], k[..., ::2]], dim=-1)k2 = k2.reshape(k.shape)# 更新kw, *对应位置相乘k = k * cos_pos + k2 * sin_posreturn q, k

老规矩，为一目了然起见，还是一步一步通过一个示例来加深理解

sinusoidal_position_embedding函数生成位置嵌入。在output_dim=512的情况下，每个位置的嵌入会有512个维度，但为了简单起见，我们只考虑前8个维度，前4个维度为sin编码，后4个维度为cos编码。所以，我们可能得到类似以下的位置嵌入

# 注意，这只是一个简化的例子，真实的位置嵌入的值会有所不同。
pos_emb = torch.tensor([[[[0.0000, 0.8415, 0.9093, 0.1411, 1.0000, 0.5403, -0.4161, -0.9900],[0.8415, 0.5403, 0.1411, -0.7568, 0.5403, -0.8415, -0.9900, -0.6536],[0.9093, -0.4161, -0.8415, -0.9589, -0.4161, -0.9093, -0.6536, 0.2836]]]])

然后，我们提取出所有的sin位置编码和cos位置编码，并在最后一个维度上每个位置编码进行复制

sin_pos = pos_emb[..., ::2].repeat_interleave(2, dim=-1)  # 提取出所有sin编码，并在最后一个维度上复制
cos_pos = pos_emb[..., 1::2].repeat_interleave(2, dim=-1)  # 提取出所有cos编码，并在最后一个维度上复制

更新query向量
我们首先构建一个新的q2向量，这个向量是由原来向量的负的cos部分和sin部分交替拼接而成的
我们用cos_pos对q进行元素级乘法，用sin_pos对q2进行元素级乘法，并将两者相加得到新的query向量

q2 = torch.stack([-q[..., 1::2], q[..., ::2]], dim=-1).flatten(start_dim=-2)
# q2: tensor([[[[-0.2,  0.1, -0.4,  0.3, -0.6,  0.5, -0.8,  0.7],
#               [-1.0,  0.9, -1.2,  1.1, -1.4,  1.3, -1.6,  1.5],
#               [-1.8,  1.7, -2.0,  1.9, -2.2,  2.1, -2.4,  2.3]]]])q = q * cos_pos + q2 * sin_pos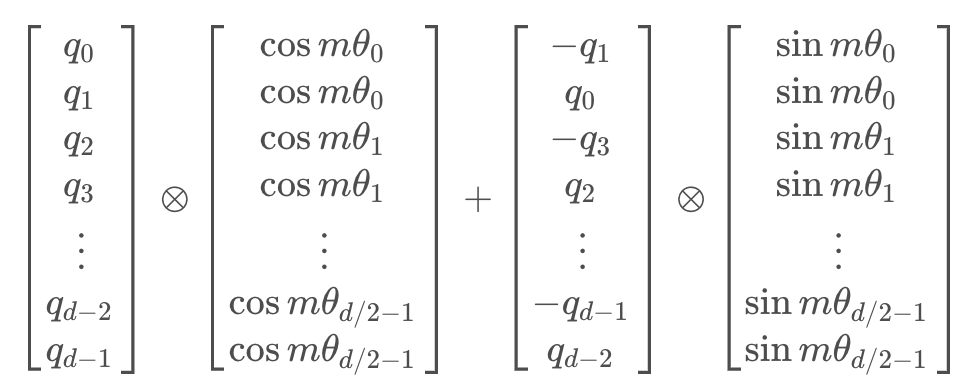

公式表示如下

更新key向量
对于key向量，我们的处理方法与query向量类似

k2 = torch.stack([-k[..., 1::2], k[..., ::2]], dim=-1).flatten(start_dim=-2)
# k2: tensor([[[[-0.15,  0.05, -0.35,  0.25, -0.55,  0.45, -0.75,  0.65

2.2.2.3 attention的编码实现

attention：这是注意力机制的主要功能

首先，如果use_RoPE被设置为True，它会应用RoPE，通过取查询和键的点积（并进行缩放）
然后，进行softmax操作来计算注意力分数，以得到概率，输出是值的加权和，权重是计算出的概率
最后，旋转后的q和k计算点积注意力后，自然就具备了相对位置信息

def attention(q, k, v, mask=None, dropout=None, use_RoPE=True):# q.shape: (bs, head, seq_len, dk)# k.shape: (bs, head, seq_len, dk)# v.shape: (bs, head, seq_len, dk)if use_RoPE:# 使用RoPE进行位置编码q, k = RoPE(q, k)d_k = k.size()[-1]# 计算注意力权重# (bs, head, seq_len, seq_len)att_logits = torch.matmul(q, k.transpose(-2, -1))  att_logits /= math.sqrt(d_k)if mask is not None:# 对权重进行mask，将为0的部分设为负无穷大att_scores = att_logits.masked_fill(mask == 0, -1e-9)  # 对权重进行softmax归一化# (bs, head, seq_len, seq_len)att_scores = F.softmax(att_logits, dim=-1)  if dropout is not None:# 对权重进行dropoutatt_scores = dropout(att_scores)# 注意力权重与值的加权求和# (bs, head, seq_len, seq_len) * (bs, head, seq_len, dk) = (bs, head, seq_len, dk)return torch.matmul(att_scores, v), att_scoresif __name__ == '__main__':# (bs, head, seq_len, dk)q = torch.randn((8, 12, 10, 32))k = torch.randn((8, 12, 10, 32))v = torch.randn((8, 12, 10, 32))# 进行注意力计算res, att_scores = attention(q, k, v, mask=None, dropout=None, use_RoPE=True)# 输出结果的形状# (bs, head, seq_len, dk),  (bs, head, seq_len, seq_len)print(res.shape, att_scores.shape)

2.2.2 LLaMA版的实现

接下来，我们再来看下LLaMA里是怎么实现这个旋转位置编码的，具体而言，LLaMA 的model.py文件里面实现了旋转位置编码(为方便大家理解，我给相关代码加了下注释)
首先，逐一实现这三个函数
precompute_freqs_cis
reshape_for_broadcast
apply_rotary_emb

# 预计算频率和复数的函数
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))    # 计算频率t = torch.arange(end, device=freqs.device)    # 根据结束位置生成序列freqs = torch.outer(t, freqs).float()    # 计算外积得到新的频率freqs_cis = torch.polar(torch.ones_like(freqs), freqs)    # 计算复数return freqs_cis    # 返回复数

# 重塑的函数
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):ndim = x.ndim    # 获取输入张量的维度assert 0 <= 1 < ndim    # 检查维度的合理性assert freqs_cis.shape == (x.shape[1], x.shape[-1])    # 检查复数的形状shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]    # 计算新的形状return freqs_cis.view(*shape)    # 重塑复数的形状并返回

# 应用旋转嵌入的函数
def apply_rotary_emb(xq: torch.Tensor,xk: torch.Tensor,freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))    # 将xq视为复数xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))    # 将xk视为复数freqs_cis = reshape_for_broadcast(freqs_cis, xq_)    # 重塑复数的形状xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)    # 计算xq的输出xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)    # 计算xk的输出return xq_out.type_as(xq), xk_out.type_as(xk)    # 返回xq和xk的输出

之后，在注意力机制的前向传播函数中调用上面实现的第三个函数 apply_rotary_emb，赋上位置信息

        # 对Query和Key应用旋转嵌入xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)