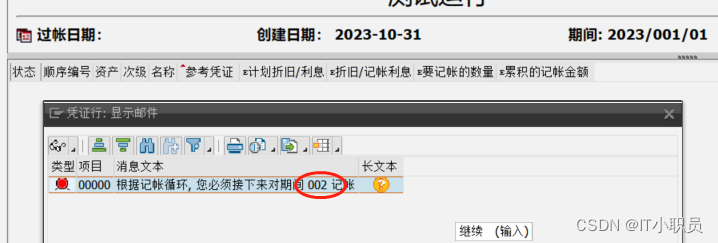
会计在运用进行固定资产折旧时,发现有个报错“根据记帐循环, 您必须接下来对期间 001记帐”,
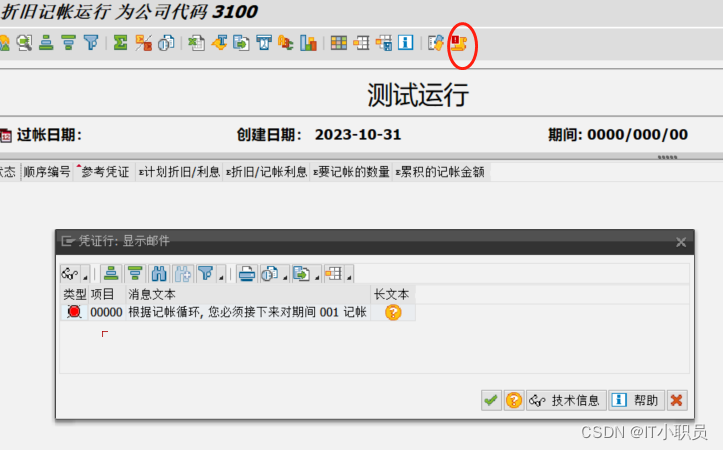
根据记帐循环, 您必须接下来对期间 001记帐
消息编号 AA683
诊断
不可以在指定的期间过帐折旧,因为此操作会遗漏过帐期间。
系统响应
该期间不能进行过帐。
步骤
根据过帐周期,应该下一个过帐期间002。或者输入对应过帐周期的期间002,或申请一个能明确为该参数运行的计划外过帐。
原因就公司地帐套是新配置(9月)的,但一直没有跑过资产折旧,而资产折旧要从本年年初开始。所以从一月份开始跑一下资产折旧就好了。
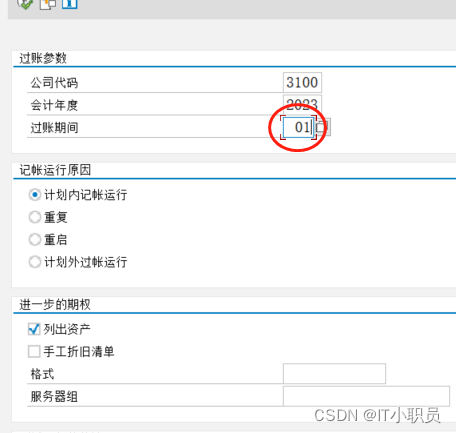
跑完之后期间变到2月了,
接下来来跑 2-10月就好了
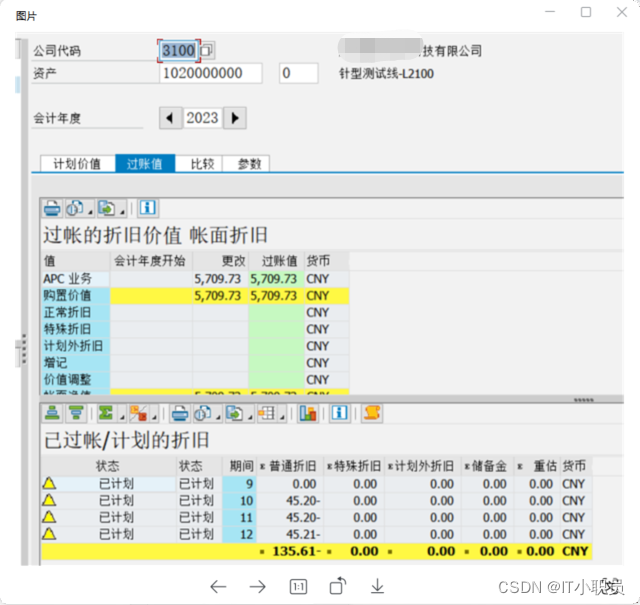
问题解决。