•  392.判断子序列 

•  115.不同的子序列  

第一题：判断子序列

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

示例 1：

• 输入：s = "abc", t = "ahbgdc"
• 输出：true

1、动态规划五部曲

（1）确定dp数组以及下标的含义

dp[i][j]表示以下标i-1为结尾的字符串s，和下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]

（2）确定递推公式

if(s[i-1]==t[j-1]) 

t中找到了一个字符在s中也出现了

if(s[i-1]!=t[j-1])

相当于当前对应元素不相同，t需要删除元素，跳到下一个元素进行匹配

if(s[i-1]==t[j-1]) 那么dp[i][j]=dp[i-1][j-1] +1;  在上一次满足条件的长度情况下加1

if(s[i-1]!=t[j-1])  此时t要删除元素，t如果把当前元素t[j-1]删除，那么dp[i][j]的数值就是看s[i-1]和t[j-2]的比较结果，即dp[i][j]=dp[i][j-1]

（3）dp数组如何初始化

 dp[i][0]肯定是没有匹配成功的值，所以为0

同理，dp[0][j]也为0

（4）确定遍历顺序

dp[i][j]依赖于dp[i-1][j-1]和dp[i][j-1]，所以从前到后遍历，先遍历s数组，然后遍历t数组

（5）举例推导

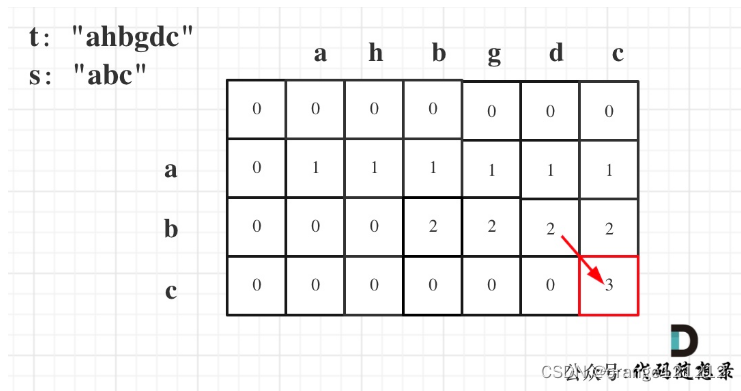
第二题：不同的子序列

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

题目数据保证答案符合 32 位带符号整数范围。

0、问题是问在字符串s中有多少种取出字符串t的方法

动态规划五部曲：

（1）确定dp数组以及下标的含义

dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]

（2）确定递推公式

s[i-1]与t[j-1]相等

s[i-1]与t[j-1]不相等

情况一：dp[i][j]=dp[i-1][j-1]+dp[i-1][j]

情况二：dp[i][j]=dp[i-1][j]  ,也就是等于以i-2为结尾的s子序列中出现j-1为结尾的t序列的个数

（3）dp数组初始化

dp[i][0]和dp[0][j]需要进行初始化

dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。

那么dp[i][0]一定都是1，因为也就是把以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1。

再来看dp[0][j]，dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数。

那么dp[0][j]一定都是0，s如论如何也变成不了t。

最后就要看一个特殊位置了，即：dp[0][0] 应该是多少。

dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t。

（4）确定遍历顺序

dp[i][j]=dp[i-1][j-1]+dp[i-1][j]或者dp[i][j]=dp[i-1][j]都是根据左上方和右上方推导出来

外层遍历s数组，内层遍历t数组

（5）举例推导

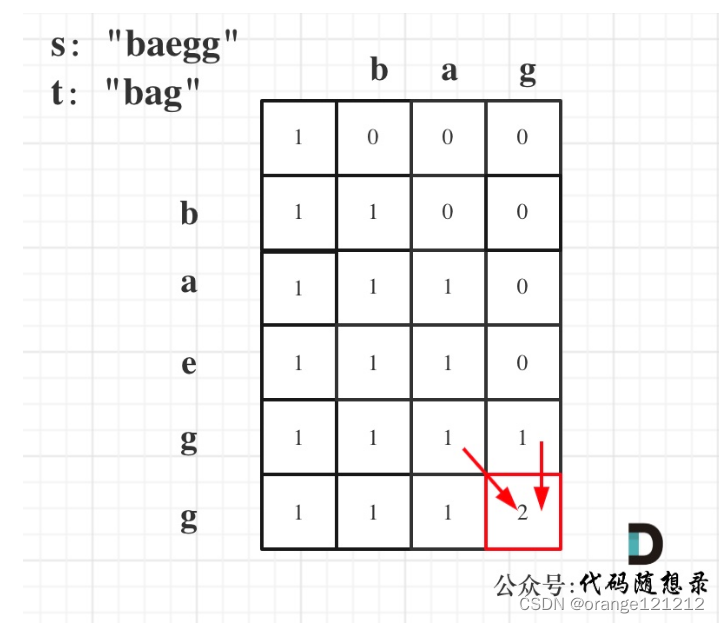
int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(s.size()+1,vector<uint64_t> (t.size()+1));for(int i=0;i<s.size();i++) dp[i][0]=1;for(int j=1;j<t.size();j++) dp[0][j]=0;for(int i=1;i<=s.size();i++){for(int j=1;j<=t.size();j++){if(s[i-1]==t[j-1]){dp[i][j]=dp[i-1][j-1]+dp[i-1][j];}else {dp[i][j]=dp[i-1][j];}}}return dp[s.size()][t.size()];}