常用数据回归建模算法总结记录-编程知识

本文的主要目的是总结记录日常学习工作中常用到的一些数据回归拟合算法，对其原理简单总结记录，同时分析对应的优缺点，以后需要的时候可以直接翻看，避免每次都要查询浪费时间，欢迎补充。

(1)线性回归 (Linear Regression)
算法构建原理：
线性回归是一种基本的回归模型，它建立了自变量与因变量之间的线性关系。算法通过拟合一个最小二乘法损失函数来找到最佳的线性拟合直线或平面。
线性回归的目标是最小化预测值与实际值之间的残差平方和。可以使用梯度下降等优化方法来求解线性回归模型的参数。
优点：
计算简单且速度快。
可解释性强，能够为结果提供可解释的权重。
对于线性关系较为明显的数据集表现良好。
缺点：
对于非线性关系的数据拟合效果较差。
对异常值和离群点敏感。
对特征之间存在共线性（多重共线性）的数据处理效果不佳。

(2)多项式回归 (Polynomial Regression)
算法构建原理：
多项式回归是在线性回归模型的基础上引入了多项式特征，以适应非线性关系的数据。通过将特征进行幂次转换，可以将问题转化为线性回归问题。
多项式回归的目标是通过增加多项式特征的维度，使模型能够更好地拟合非线性关系。
优点：
能够拟合复杂的非线性关系。
灵活性较高，在选择合适的特征次数后，能够更好地适应数据。
缺点：
高次项的引入会导致参数数量增加，容易出现过拟合。
特征转换的选择需要经验或者试验，对于高阶多项式，可能会出现维度爆炸的问题。

(3)支持向量回归 (Support Vector Regression, SVR)
算法构建原理：
支持向量回归是在支持向量机算法的框架下进行回归任务的方法。它使用支持向量机的核函数和间隔最大化的原则来拟合曲线或超平面。
SVR的目标是找到一个边界（超平面），使得真实值尽可能地落在超平面内，并且最小化预测误差。
优点：
可以处理非线性关系的数据。
通过核函数的选择，可以扩展到高维空间。
对于异常值和离群点具有一定的鲁棒性。
缺点：
对于数据量较大的情况，训练时间较长。
参数选择相对较多，需要进行调优。
对于特征缩放和参数调节比较敏感。

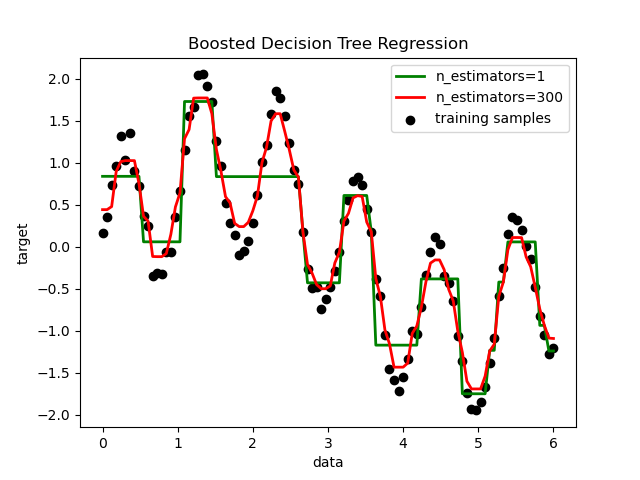
(4)决策树回归 (Decision Tree Regression)
算法构建原理：
决策树回归使用决策树模型进行回归预测。它通过递归地选择最佳的特征进行划分，构建一个树结构来完成回归任务。
决策树通过将样本根据特征值划分为不同的叶节点，并以叶节点中样本的均值作为预测值。
优点：
非常直观且易于解释，能够提供可解释的决策规则。
能够处理非线性关系和复杂模式的数据。
对于离散型和连续型特征都能有效处理。
缺点：
容易产生过拟合，特别是在处理高维数据时。
对于噪声较大的数据，容易产生不稳定的预测结果。
对于数据集中类别不平衡的情况，可能会生成有偏的树结构。

(5)MLP回归 (Multi-Layer Perceptron Regression)
算法构建原理：
MLP回归是一种基于人工神经网络的回归算法。它由多个神经元组成的多层网络，每个神经元都与前一层的每个神经元相连。
MLP回归通过前向传播将输入数据通过各个层级进行加权、变换和激活，最后输出预测结果。
优点：
能够处理非线性关系和复杂模式的数据。
具有较强的表达能力，可以处理高度复杂的问题。
在大规模数据集上表现良好，可以通过深度学习方法进行端到端的训练。
缺点：
对于小型数据集和少量样本，容易过拟合。
训练复杂的神经网络可能需要大量的计算资源和时间。
参数调整相对较多，需要进行调优。

(6)高斯回归 (Gaussian Regression)
算法构建原理：
高斯回归是一种回归模型，假设目标变量服从高斯分布。它通过最大似然估计来拟合数据，并使用高斯分布来预测连续型目标变量的值。
高斯回归模型假设输入特征与目标变量之间的关系是线性的，但目标变量的噪声项是符合高斯分布的。
优点：
在处理连续型目标变量时表现良好。
可以提供可解释的权重和置信区间。
对于噪声较小的数据，可以获得较好的预测结果。
缺点：
对于非线性关系的数据拟合效果较差。
对异常值和离群点比较敏感。
对特征之间存在共线性（多重共线性）的数据处理效果不佳。

(7)K近邻回归 (K-Nearest Neighbors Regression)
算法构建原理：
K近邻回归是一种基于实例的回归算法，它通过找到与待预测样本最接近的K个训练样本，然后根据这K个样本的平均值或加权平均值来进行回归预测。
计算距离：计算待预测样本与每个训练样本之间的距离（通常使用欧氏距离或曼哈顿距离）。
选择K个近邻：从所有训练样本中选择与待预测样本最近的K个样本。
回归预测：对于回归问题，通过K个近邻的输出值（目标变量）的平均值或加权平均值作为待预测样本的预测结果。
优点：
简单直观，易于实现和理解。
能够处理非线性关系和复杂模式的数据。
对于离群值不敏感，能够在数据中捕捉到局部的模式。
缺点：
对于大规模数据集，计算开销较大。
预测速度相对较慢，特别是当特征维度较高时。
对于特征的缩放敏感，需要进行特征归一化处理。
K近邻回归的性能受到超参数K的影响。较小的K值会使模型更加敏感，容易受到噪声的影响，而较大的K值会使模型变得平滑，但可能损失了局部模式的捕捉能力。因此，在使用K近邻回归时需要仔细选择合适的K值以获得良好的预测性能。

(8)随机梯度下降回归 (Stochastic Gradient Descent Regression)
算法构建原理：
随机梯度下降回归是一种基于优化算法的回归方法。它通过不断迭代更新模型参数，最小化损失函数来拟合数据。
随机梯度下降回归每次只使用一个样本或一个小批量样本来计算梯度，并根据学习率和梯度方向来更新模型参数。
优点：
训练速度快，尤其适用于大规模数据集。
相对简单易懂，不涉及复杂的矩阵运算。
对于在线学习和增量学习有较好的适应性。
缺点：
对于非凸损失函数，可能会陷入局部最优解。
参数调整较多，需要进行学习率和正则化项的调优。
对于特征的缩放敏感，需要进行特征归一化处理。

(9)朴素贝叶斯回归 (Naive Bayes Regression)
算法构建原理：
朴素贝叶斯回归是一种基于贝叶斯定理的回归方法。它假设输入特征之间相互独立，并利用贝叶斯定理计算后验概率来进行回归预测。
朴素贝叶斯回归通过估计先验概率和条件概率来计算后验概率，进而得到预测结果。
优点：
计算简单高效，适用于大规模数据集。
在输入特征之间存在强独立性假设时，表现良好。
对于分类问题，具有较好的鲁棒性和稳定性。
缺点：
对于输入特征之间的依赖关系无法建模。
假设特征之间相互独立，不适用于特征相关性较强的数据。
对于输入特征中存在缺失值时，处理相对复杂。

(10)随机森林回归 (Random Forest Regression)
算法构建原理：
随机森林回归是在随机森林算法的基础上进行回归任务的方法。它通过构建多个决策树来预测结果，并将它们的平均值作为最终的预测值。
随机森林使用自助采样和特征随机选择的方法来构建每个决策树，并通过投票或平均结果来得出最终的回归结果。
优点：
能够处理高维数据和大规模数据集。
对于缺失数据和离群点具有一定的鲁棒性。
在处理非线性关系和复杂模式时表现良好。
缺点：
对于噪声较大的数据，可能会导致过拟合。
参数调整较多，需要进行调优。
随机森林的训练时间较长。

(11)梯度提升回归 (Gradient Boosting Regression)
算法构建原理：
梯度提升回归也是一种集成学习方法，通过逐步迭代训练弱回归模型来提升整体性能。它通过减小残差的梯度方向来拟合数据。
梯度提升回归通过构建一个序列的弱回归模型（通常是决策树），并使用梯度下降法迭代地优化损失函数。
优点：
在处理复杂非线性关系和大规模数据时表现出色。
对于异常值和噪声具有一定的鲁棒性。
可以处理各种类型的特征，包括离散和连续特征。
缺点：
参数调整相对较多，需要进行调优。
对于高维稀疏数据集可能不够高效。

(12)XGBoost回归
算法构建原理：
XGBoost (eXtreme Gradient Boosting) 回归是一种基于梯度提升算法的集成学习方法。它通过优化损失函数的梯度来逐步训练弱回归模型，并通过加权求和得到最终的预测结果。
XGBoost采用了一些特殊的技术（如正则化、剪枝等）来增加模型的泛化能力和鲁棒性。
优点：
在大规模数据集上表现出色，具有高效性能。
对于非线性关系和复杂模式的数据具有很好的拟合能力。
可以处理各种类型的特征，包括离散和连续特征。
缺点：
对于异常值和噪声敏感。
参数调整较多，需要进行调优。

(13)LightGBM回归
算法构建原理：
LightGBM 是一种基于梯度提升算法的集成学习方法，用于回归任务。它采用了基于叶子分割（Leaf-wise）的决策树生长方式，在保证准确性的同时提高了效率。
LightGBM引入了直方图算法和互斥特征捆绑等技术来加速训练过程，并通过引入最大叶节点数和层级限制等参数
优点：
在大规模数据集上表现出色，具有高效性能。
对于非线性关系和复杂模式的数据具有很好的拟合能力。
可以处理各种类型的特征，包括离散和连续特征。
在处理高维稀疏数据时能够更好地处理。
缺点：
对于异常值和噪声敏感。
参数调整较多，需要进行调优。

(14)神经网络回归
算法构建原理：
神经网络回归使用神经网络模型进行回归预测。神经网络可以通过堆叠多个层次、非线性激活函数和优化算法来拟合复杂的非线性关系。
神经网络回归通过前向传播将输入数据通过各个层级进行加权、变换和激活，最后输出预测结果。
优点：
能够适应各种非线性关系和复杂模式的数据。
具有较强的表达能力，可以处理高度复杂的问题。
在大规模数据集上表现良好，可以通过深度学习方法进行端到端的训练。
缺点：
训练复杂的神经网络可能需要大量的计算资源和时间。
需要大量的数据进行训练，容易出现过拟合。
参数调整相对较多，需要进行调优。

下面是Demo代码实现，可以参考使用即可：

【机器学习模型】

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.svm import SVR
from sklearn.tree import DecisionTreeRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import SGDRegressor
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor# 生成分类数据集
X, y = make_classification(n_samples=1000, n_features=10, random_state=42)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 线性回归
linear_reg = LinearRegression()
linear_reg.fit(X_train, y_train)# 多项式回归
poly_features = PolynomialFeatures(degree=2)
X_train_poly = poly_features.fit_transform(X_train)
poly_reg = LinearRegression()
poly_reg.fit(X_train_poly, y_train)# 支持向量回归
svr = SVR()
svr.fit(X_train, y_train)# 决策树回归
dt_reg = DecisionTreeRegressor()
dt_reg.fit(X_train, y_train)# MLP回归
mlp_reg = MLPRegressor()
mlp_reg.fit(X_train, y_train)# 高斯回归
gaussian_reg = GaussianProcessRegressor()
gaussian_reg.fit(X_train, y_train)# K近邻回归
knn_reg = KNeighborsRegressor()
knn_reg.fit(X_train, y_train)# 随机梯度下降回归
sgd_reg = SGDRegressor()
sgd_reg.fit(X_train, y_train)# 朴素贝叶斯回归
nb_reg = GaussianNB()
nb_reg.fit(X_train, y_train)# 随机森林回归
rf_reg = RandomForestRegressor()
rf_reg.fit(X_train, y_train)# 梯度提升回归
gb_reg = GradientBoostingRegressor()
gb_reg.fit(X_train, y_train)# XGBoost回归
xgb_reg = XGBRegressor()
xgb_reg.fit(X_train, y_train)# LightGBM回归
lgb_reg = LGBMRegressor()
lgb_reg.fit(X_train, y_train)

【深度学习模型】

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense# 生成分类数据集
X, y = make_classification(n_samples=1000, n_features=10, random_state=42)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 特征缩放
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 构建深度学习模型
model = Sequential()
model.add(Dense(64, activation='relu', input_shape=(X_train.shape[1],)))
model.add(Dense(32, activation='relu'))
model.add(Dense(1, activation='sigmoid'))# 编译模型
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])# 训练模型
model.fit(X_train_scaled, y_train, epochs=10, batch_size=32, validation_data=(X_test_scaled, y_test))