详细认识二叉树【图片+代码】

目录

一、树的概念及结构

1.1树的概念

1.2树的相关概念

1.3树的表示

1.4树在实际中的应用（目录树） 

二、二叉树概念及结构

2.1概念

2.2特殊的二叉树

2.3二叉树的性质 

2.4二叉树存储结构

三、二叉树的顺序结构及实现

3.1二叉树的顺序结构

3.2堆的结构及概念

四、二叉树的链式结构及实现

五、二叉树的遍历（前序、中序、后序、层序遍历）

5.1前序遍历

5.2中序遍历

5.3后序遍历

5.4层序遍历

六、求二叉树的节点个数、叶子节点个数、高度、查找节点等功能

6.1二叉树节点的个数

6.2二叉树叶子节点的个数

6.3二叉树的高度

6.4二叉树第K层节点的个数

6.5查找节点

6.6二叉树度为1的节点个数

七、创建二叉树、销毁二叉树

7.1创建二叉树

7.2销毁二叉树

八、判断二叉树是否为完全二叉树

九、OJ练习——二叉树部分

9.1检查两颗树是否相同

9.2单值二叉树

9.3翻转二叉树

9.4对称二叉树

9.5另一颗数的子树

9.6判断一颗二叉树是否是平衡二叉树

一、树的概念及结构

1.1树的概念

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因 为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
  • 有一个特殊的结点，称为根结点，根节点没有前驱结点。
  • 除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继。
  • 因此，树是递归定义的。

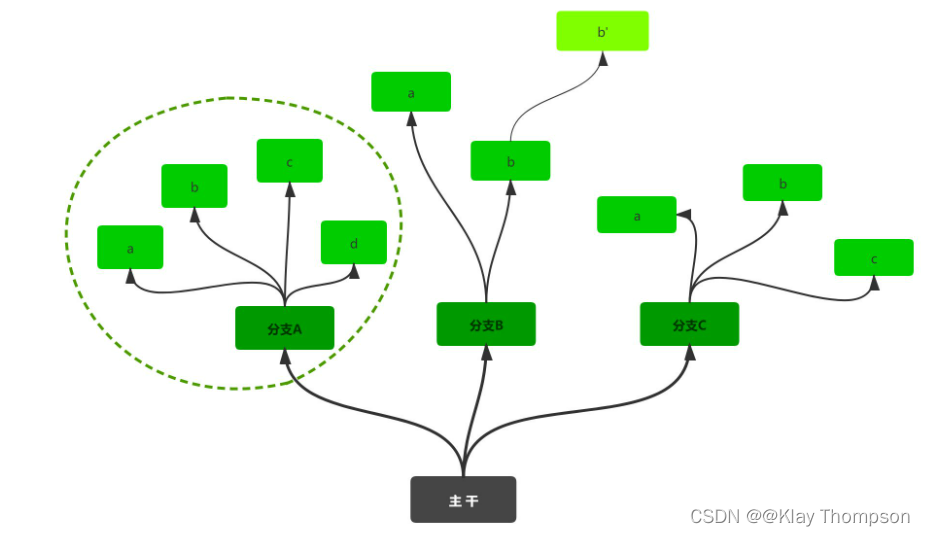
1.2树的相关概念

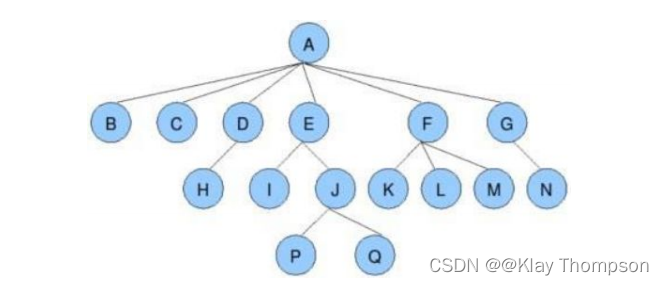
  1. 节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为6
  2. 叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I...等节点为叶节点
  3. 非终端节点或分支节点：度不为0的节点； 如上图：D、E、F、G...等节点为分支节点
  4. 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点
  5. 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点
  6.  兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点 
  7. 树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为6
  8. 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
  9. 树的高度或深度：树中节点的最大层次； 如上图：树的高度为4
  10. 堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
  11. 节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先
  12. 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
  13. 森林：由m（m>0）棵互不相交的树的集合称为森林；

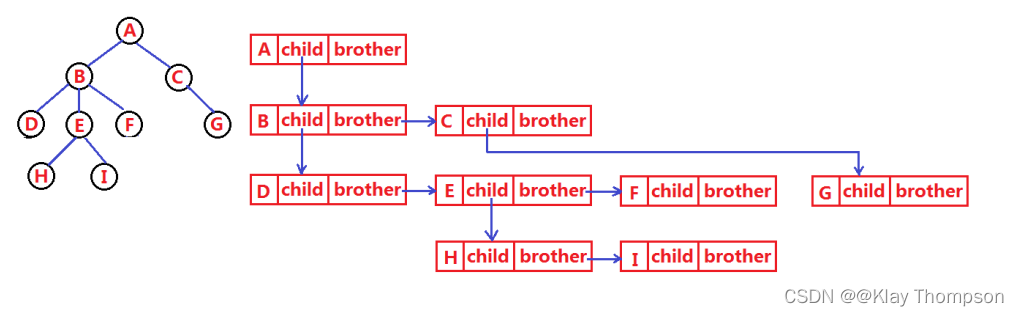
1.3树的表示

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，既然保存值域，也要保存结点和结点之间 的关系，实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。
typedef int DataType;
struct Node
{
struct Node* _firstChild1;                 // 第一个孩子结点
struct Node* _pNextBrother;            // 指向其下一个兄弟结点
DataType _data;                               // 结点中的数据域
};

1.4树在实际中的应用（目录树） 

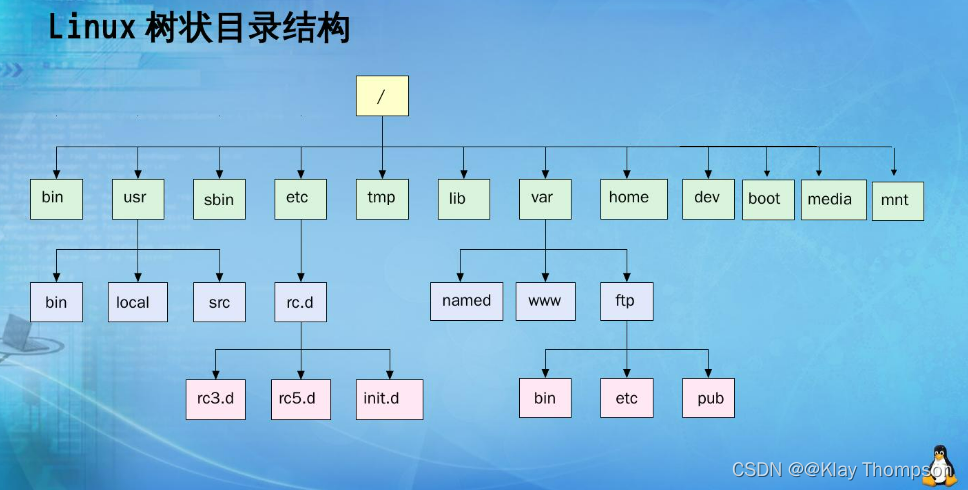
二、二叉树概念及结构

2.1概念

一棵二叉树是结点的一个有限集合，该集合:
  1. 或者为空
  2. 由一个根节点加上两颗别称为左子树和右子树的二叉树组成

注意： 

  1. 二叉树不存在度大于2的节点
  2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树
  3. 对于任意的二叉树都是由以下几种情况复合而成的：

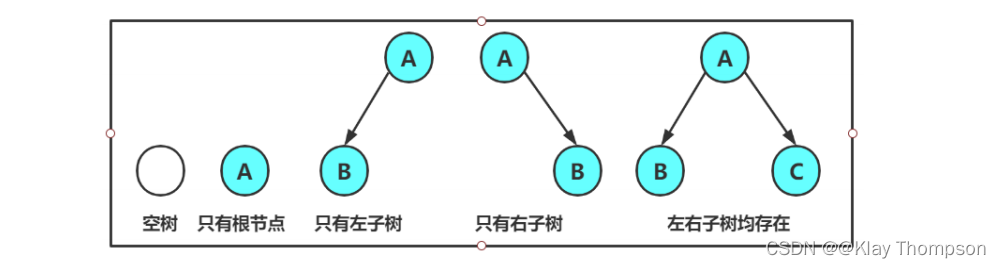
2.2特殊的二叉树

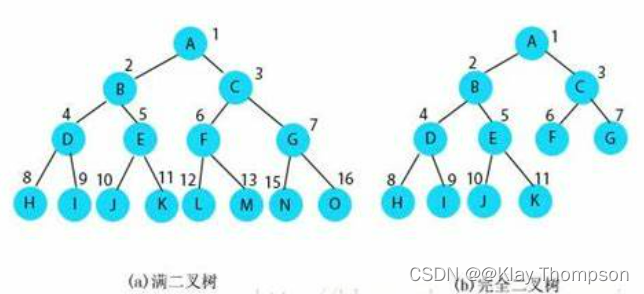
  1. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是2^k - 1，则它就是满二叉树。
  2. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

2.3二叉树的性质 

2.4二叉树存储结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。
        1.顺序存储：顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为
                             不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储关
                             于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组，在逻辑
                              上是一颗二叉树。

         2.链式存储：二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的                               逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域                               左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。

                             链式结构又分为二叉链和三叉链，当前我们学习中一般都是二叉链。

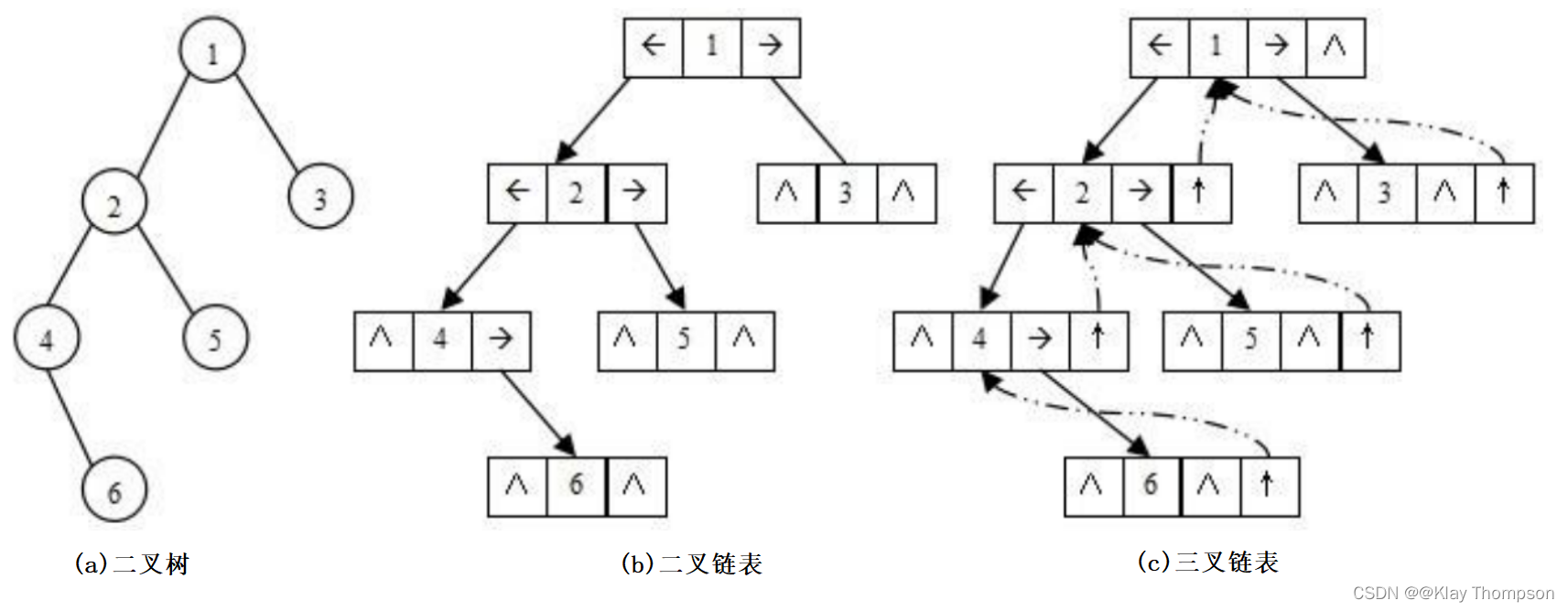
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
        struct BinTreeNode* _pLeft;         // 指向当前节点左孩子
        struct BinTreeNode* _pRight;       // 指向当前节点右孩子
        BTDataType _data;                       // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{
        struct BinTreeNode* _pParent;         // 指向当前节点的双亲
        struct BinTreeNode* _pLeft;              // 指向当前节点左孩子
        struct BinTreeNode* _pRight;            // 指向当前节点右孩子
        BTDataType _data;                            // 当前节点值域
}；

三、二叉树的顺序结构及实现

3.1二叉树的顺序结构

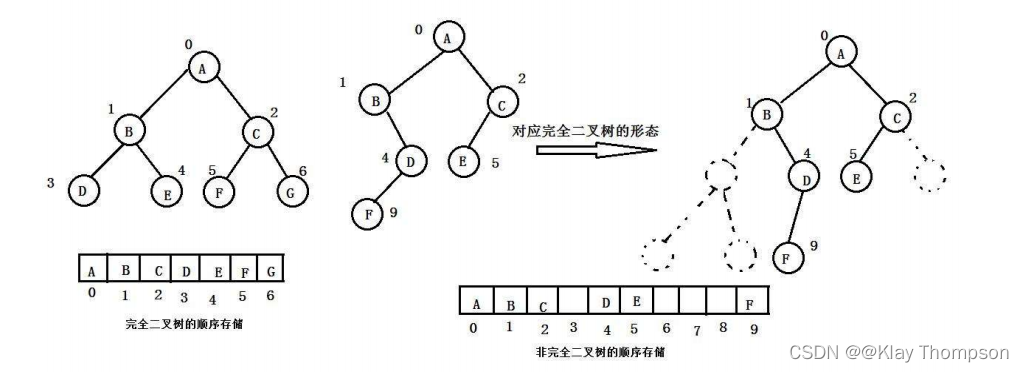
普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

3.2堆的结构及概念

有关堆的结构及概念，堆的实现和应用，请看上一篇：http://t.csdn.cn/Dbj44

四、二叉树的链式结构及实现

树的简单的创建：

typedef int BTDataType;
typedef struct BinaryTreeNode
{
        BTDataType _data;
        struct BinaryTreeNode* _left;
        struct BinaryTreeNode* _right;
}BTNode;
BTNode* CreatBinaryTree()
{
        BTNode* node1 = BuyNode(1);
        BTNode* node2 = BuyNode(2);
        BTNode* node3 = BuyNode(3);
        BTNode* node4 = BuyNode(4);
        BTNode* node5 = BuyNode(5);
        BTNode* node6 = BuyNode(6);
        node1->_left = node2;
        node1->_right = node4;
        node2->_left = node3;
        node4->_left = node5;
        node4->_right = node6;
        return node1;
}

五、二叉树的遍历（前序、中序、后序、层序遍历）

5.1前序遍历

前序遍历——访问根结点的操作发生在遍历其左右子树之前。

代码：

void PrevOrder(TNode* root)
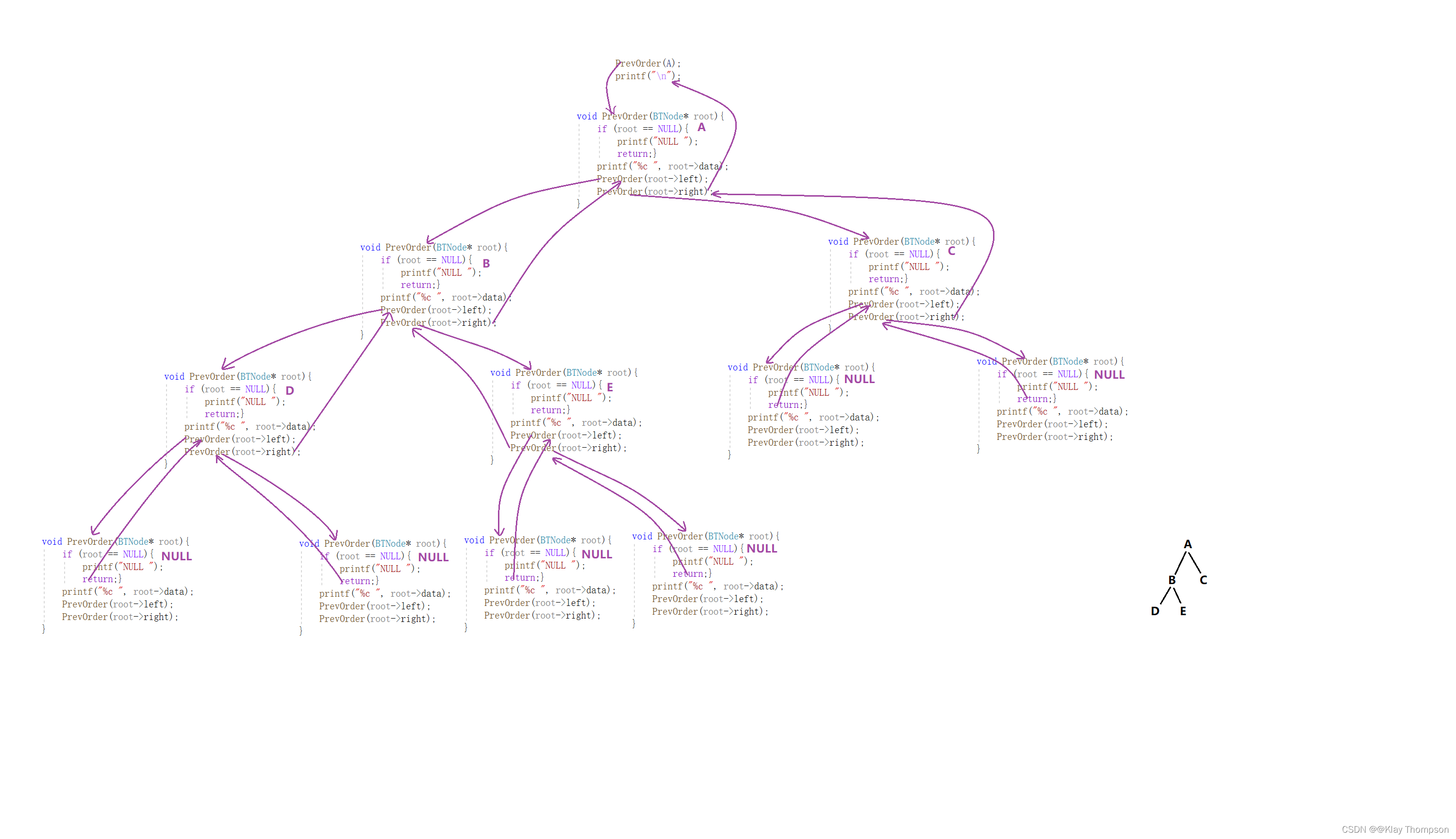
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->lchild);PrevOrder(root->rchild);
}

递归展开图：

5.2中序遍历

中序遍历——访问根结点的操作发生在遍历其左右子树之中（间）。

代码：

void InOrder(TNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->lchild);printf("%d ", root->data);InOrder(root->rchild);
}

递归展开图：

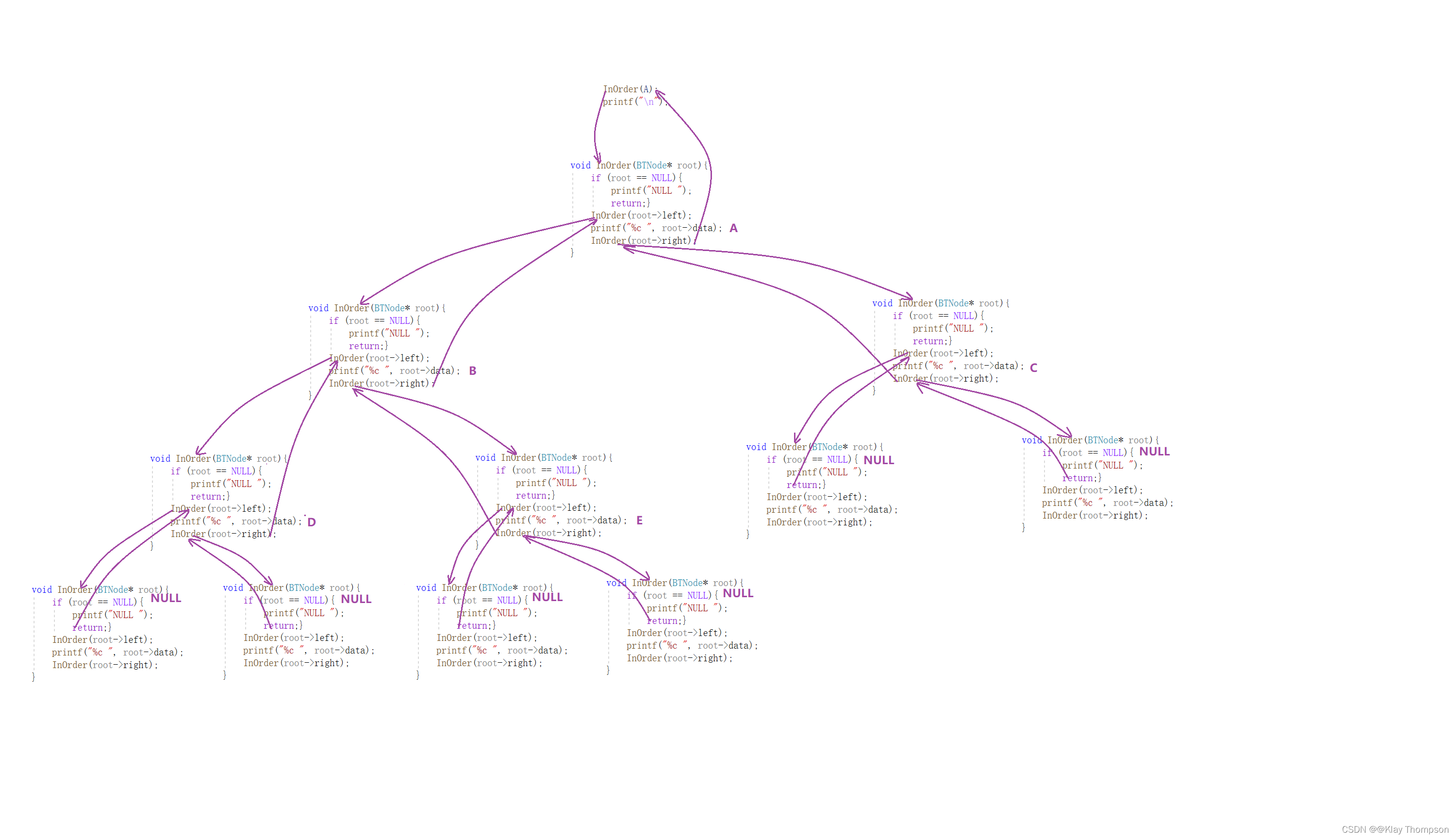
5.3后序遍历

后序遍历——访问根结点的操作发生在遍历其左右子树之后。

代码：

void PostOrder(TNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->lchild);PostOrder(root->rchild);printf("%d ", root->data);
}

递归展开图：

5.4层序遍历

层序遍历——设二叉树的根节点所在 层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层 上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

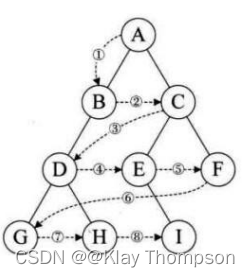
 层序遍历思想：要借助队列来完成，将根节点入队列，然后开始循环，若队列为空就循环结束，每次出来队头的数据，在队头的数据出去之后要立即将出去的那个节点的孩子入队列（孩子为空就不入队列）

代码：

void LevelOrder(TNode* root)
{if (root == NULL){return;}Queue q;QueueInit(&q);//进队列QueuePush(&q, root);while (!QueueEmpty(&q)){TNode* node = QueueFront(&q);QueuePop(&q);printf("%d ", node->data);if (node->lchild)QueuePush(&q, node->lchild);if (node->rchild)QueuePush(&q, node->rchild);}printf("\n");
}

六、求二叉树的节点个数、叶子节点个数、高度、查找节点等功能

6.1二叉树节点的个数

int BTreeSize(TNode* root)
{if (root == NULL){return 0;}return BTreeSize(root->lchild) + BTreeSize(root->rchild) + 1;
}

6.2二叉树叶子节点的个数

int BTreeLeafSize(TNode* root)
{if (root == NULL){return 0;}if (root->lchild == NULL && root->rchild == NULL){return 1;}return BTreeLeafSize(root->lchild) + BTreeLeafSize(root->rchild);
}

6.3二叉树的高度

int BTreeHeight(TNode* root)
{if (root == NULL){return 0;}int leftHeight = BTreeHeight(root->lchild);int rightHeight = BTreeHeight(root->rchild);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

6.4二叉树第K层节点的个数

int BTreeLevelKSize(TNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BTreeLevelKSize(root->lchild, k - 1) + BTreeLevelKSize(root->rchild, k - 1);}

6.5查找节点

TNode* BTreeFind(TNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}TNode* left = BTreeFind(root->lchild, x);if (left)return left;TNode* right = BTreeFind(root->rchild, x);if (right)return right;return NULL;
}

6.6二叉树度为1的节点个数

int BTreeDeg1Size(TNode* root)
{if (root == NULL){return 0;}int left = BTreeDeg1Size(root->lchild);int right = BTreeDeg1Size(root->rchild);if ((root->lchild == NULL && root->rchild != NULL)|| (root->lchild != NULL && root->rchild == NULL)){return left + right + 1;}else{return left + right;}
}

七、创建二叉树、销毁二叉树

7.1创建二叉树

 

TNode* TCreateTree(char* tree, int* pi)
{if (tree[*pi] == '#'){(*pi)++;return NULL;}TNode* root = (TNode*)malloc(sizeof(TNode));root->data = tree[*pi];(*pi)++;root->lchild = TCreateTree(tree, pi);root->rchild = TCreateTree(tree, pi);return root;
}

7.2销毁二叉树

void DestoryTree(TNode* root)
{if (root == NULL){return;}DestoryTree(root->lchild);DestoryTree(root->rchild);free(root);
}

八、判断二叉树是否为完全二叉树

借助队列，将一个二叉树层序遍历进入队列，遇到NULL也进入队列，直到出队列时遇到NULL停止，判断此时队列中是否存在非NULL元素，如果存在，不是完全二叉树，如果全为NULL，是完全二叉树。

bool BTreeComplete(TNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){TNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueuePush(&q, front->lchild);QueuePush(&q, front->rchild);}else{break;}}while (!QueueEmpty(&q)){TNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestory(&q);return false;}}QueueDestory(&q);return true;
}

九、OJ练习——二叉树部分

9.1检查两颗树是否相同

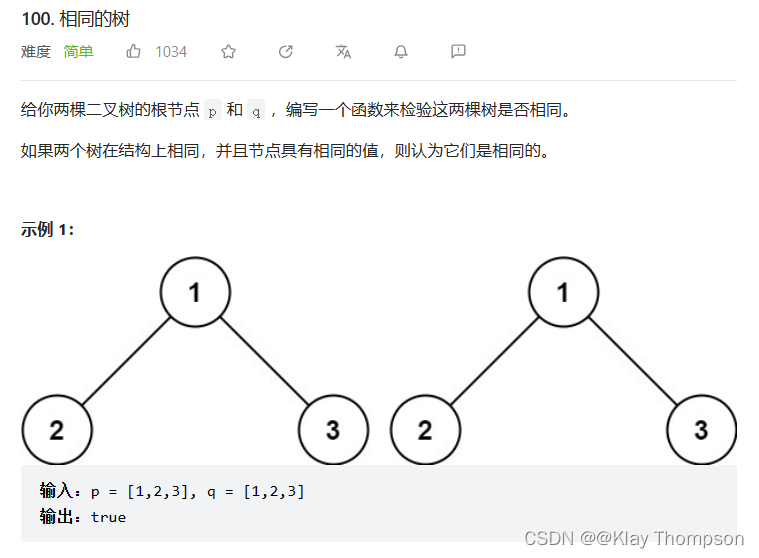
bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p == NULL && q == NULL){return true;}if(p == NULL || q == NULL){return false;}if(p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

 

9.2单值二叉树

bool isUnivalTree(struct TreeNode* root){if(root == NULL){return true;}if(root->left!= NULL && root->val != root->left->val){return false;}if(root->right!= NULL && root->val != root->right->val){return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);
}

9.3翻转二叉树

struct TreeNode* invertTree(struct TreeNode* root){if(root == NULL){return NULL;}//保存一下原来的左孩子struct TreeNode* left = root->left;root->left = invertTree(root->right);root->right = invertTree(left);return root;
}

9.4对称二叉树

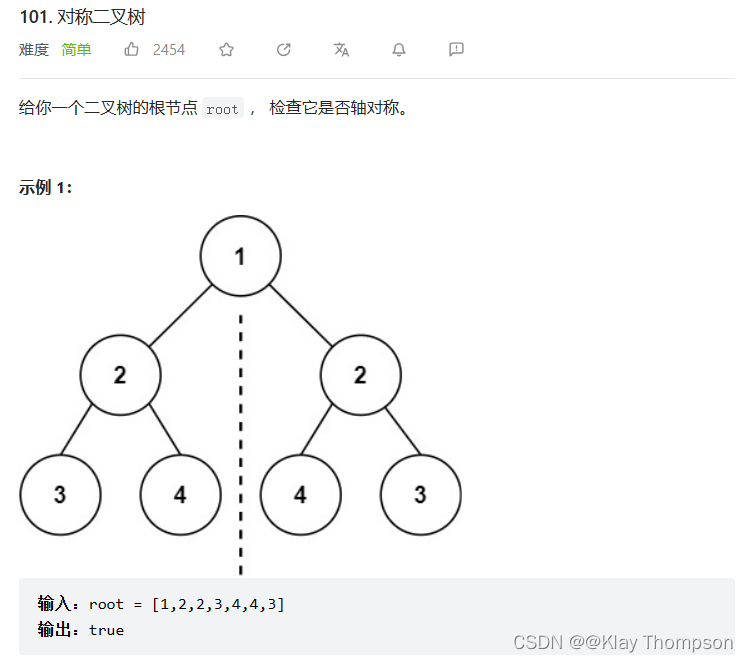
bool _isSymmetric(struct TreeNode* r1, struct TreeNode* r2)
{if(r1 == NULL && r2 == NULL){return true;}if(r1 == NULL || r2 == NULL){return false;}if(r1->val != r2->val){return false;}return _isSymmetric(r1->left, r2->right) && _isSymmetric(r1->right, r2->left);
}bool isSymmetric(struct TreeNode* root){return _isSymmetric(root->left, root->right);
}

9.5另一颗数的子树

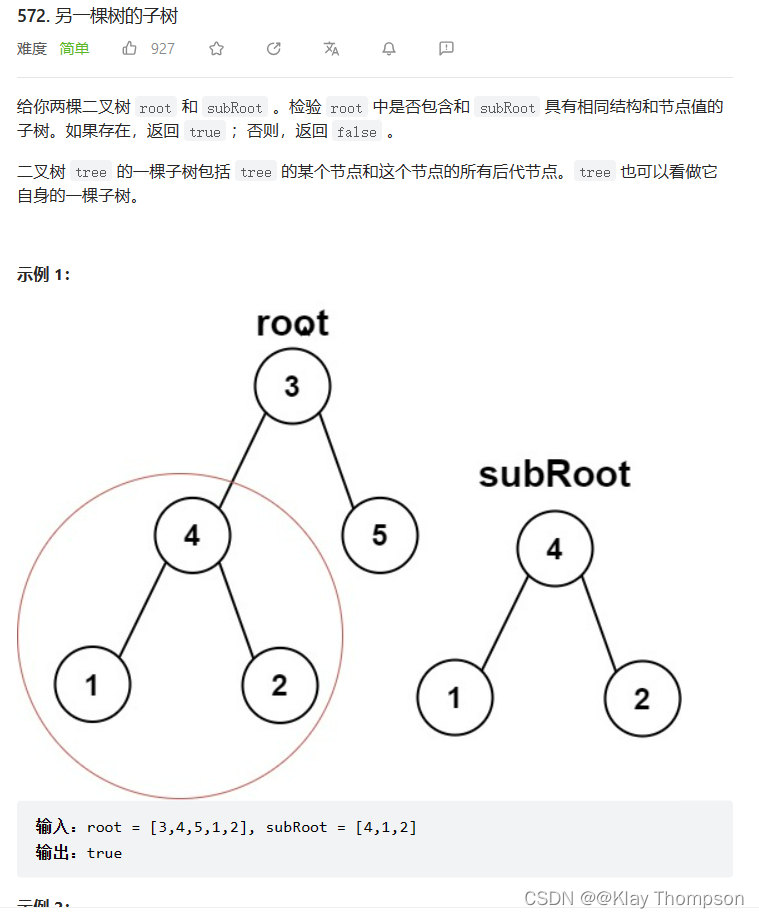
bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p == NULL && q == NULL){return true;}if(p == NULL || q == NULL){return false;}if(p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root == NULL && subRoot == NULL){return true;}if(root == NULL || subRoot == NULL){return false;}if(isSameTree(root, subRoot)){return true;}return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

9.6判断一颗二叉树是否是平衡二叉树

 

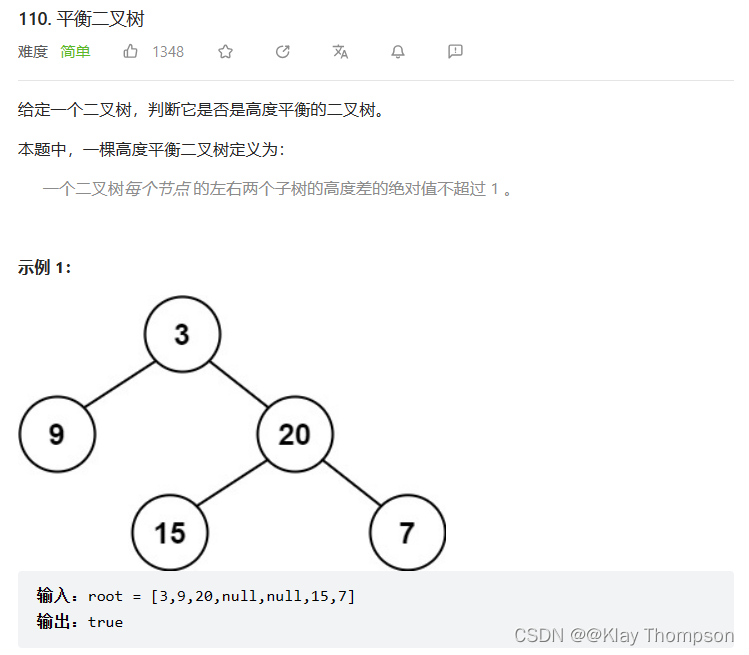
int BTreeHeight(struct TreeNode* root)
{if (root == NULL){return 0;}int leftHeight = BTreeHeight(root->left);int rightHeight = BTreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}bool isBalanced(struct TreeNode* root){if(root == NULL){return true;}int left = BTreeHeight(root->left);int right = BTreeHeight(root->right);int sub = abs(left - right);if(sub > 1){return false;}return isBalanced(root->left) && isBalanced(root->right);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/1605.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

初探 C++ 标准库

初探 C++ 标准库

有趣的重载 重载左移操作符&#xff0c;将变量或常量左移到一个对象中&#xff01; C 标准库 C 标准库并不是 C 语言的一部分 C 标准库是由类库和函数库组成的集合 C 标准库中定义的类和对象都位于 std 命名空间中 C 标准库的头文件都不带 .h 后缀 C 标准库涵盖了 C 库的功…
阅读更多...
6、多层感知机：数值稳定性和模型初始化

6、多层感知机：数值稳定性和模型初始化

1、数值稳定性 考虑一个具有 L L L层、输入 x \mathbf{x} x和输出 o \mathbf{o} o的深层网络。每一层 l l l由变换 f l f_l fl​定义&#xff0c;该变换的参数为权重 W ( l ) \mathbf{W}^{(l)} W(l)&#xff0c;其隐藏变量是 h ( l ) \mathbf{h}^{(l)} h(l)&#xff08;令 h …
阅读更多...
人工智能(pytorch)搭建模型14-pytorch搭建Siamese Network模型(孪生网络)，实现模型的训练与预测

人工智能(pytorch)搭建模型14-pytorch搭建Siamese Network模型(孪生网络)，实现模型的训练与预测

大家好&#xff0c;我是微学AI&#xff0c;今天给大家介绍一下人工智能(pytorch)搭建模型14-pytorch搭建Siamese Network模型(孪生网络)&#xff0c;实现模型的训练与预测。孪生网络是一种用于度量学习&#xff08;Metric Learning&#xff09;和比较学习&#xff08;Compariso…
阅读更多...
Windows环境本地部署Oracle11g r2实操手册

Windows环境本地部署Oracle11g r2实操手册

前言&#xff1a;一直在做其他测试&#xff0c;貌似都忘了Windows环境oracle安装&#xff0c;这是一个很早很早的安装记录了&#xff0c;放上来做个备录给到大家参考。 环境&#xff1a; &#xff08;都是常规系统及工具&#xff0c;官网度娘搜索即可下载测试学习&#xff09;…
阅读更多...
移动机器人底盘-四轮差速模型（四轮独立）

移动机器人底盘-四轮差速模型（四轮独立）

移动机器人底盘-四轮差速模型 文章目录 移动机器人底盘-四轮差速模型1. 四轮差速模型原理2. 工程实践2.1 Python实现2.2 C实现 1. 四轮差速模型原理 四轮差速模型底盘实例如下图所示。对于底盘的前轮和后轮来说&#xff0c;其速度是同步的&#xff0c;那么在理想条件下&#x…
阅读更多...
【鲁棒优化】微电网鲁棒优化定价方案研究（Matlab代码实现）

【鲁棒优化】微电网鲁棒优化定价方案研究（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…
阅读更多...
中间件漏洞解析

中间件漏洞解析

服务器解析漏洞算是历史比较悠久了&#xff0c;但如今依然广泛存在。在此记录汇总一些常见服务器&#xff08;WEB server&#xff09;的解析漏洞&#xff0c;比如IIS6.0、IIS7.5、apache、nginx等 2|0 二、IIS5.x-6.x解析漏洞&#xff08;针对asa/asp/cer&#xff09; 2|11、打…
阅读更多...
HTTP协议

HTTP协议

HTTP协议专门用于定义浏览器与服务器之间交互数据的过程以及数据本身的格式 HTTP概述 HTTP是一种客户端&#xff08;用户&#xff09;请求和服务器&#xff08;网站&#xff09;应答的标准&#xff0c;它作为一种应用层协议&#xff0c;应用于分布式、协作式和超媒体信息系统…
阅读更多...
FTP服务器

FTP服务器

文章目录 FTP服务器FTP的数据传输原理FTP的功能简介不同等级的用户身份命令记录与日志文件记录限制用户活动的目录 FTP的工作流程与使用到的端口FTP主动式连接FTP被动式连接 vsftpd服务器基础设置为什么使用vsftpd所需要的软件以及软件结构vsftpd.conf 配置值说明与服务器环境比…
阅读更多...
Spring Data JPA 报 HOUR_OF_DAY: 0 -＞ 1异常的解决过程和方案

Spring Data JPA 报 HOUR_OF_DAY: 0 -＞ 1异常的解决过程和方案

在进行数据查询时&#xff0c;控制台报了Caused by: com.mysql.cj.exceptions.WrongArgumentException: HOUR_OF_DAY: 0 -> 1异常&#xff0c;查询得知&#xff1a;这是由于查mysql库&#xff0c;转换类型为datetime类型的字段引起的。 网上的解决方案有多种&#xff0c;大…
阅读更多...
SIGGRAPH 2023｜你的AI Tony老师上线了，英伟达提出毛发模拟新基线

SIGGRAPH 2023｜你的AI Tony老师上线了，英伟达提出毛发模拟新基线

2018年&#xff0c;网易《逆水寒》与AMD合作开发出来一款名为“海飞丝”的算法&#xff0c;该算法基于AMD的TressFX毛发模拟技术&#xff0c;可以在游戏中较为清晰的模拟人类头发的运动&#xff0c;大大增强了游戏场景的真实感。一个健康的成年人大概拥有10万根头发&#xff0c…
阅读更多...
thinkphp 反序列化漏洞

thinkphp 反序列化漏洞

文章目录 配置xdebug反序列化漏洞利用链详细分析poc1&#xff08;任意文件删除&#xff09;poc2&#xff08;任意命令执行&#xff09; 补充代码 配置xdebug php.ini [Xdebug] zend_extensionD:/phpstudy_pro/Extensions/php/php7.3.4nts/ext/php_xdebug.dll xdebug.modedebu…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023