435.无重叠区间

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

示例 1:

输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:

输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

提示:

• 1 <= intervals.length <= 10^5
• intervals[i].length == 2
• -5 * 10^4 <= starti < endi <= 5 * 10^4

思路

本题和上一题的引爆气球有点像，也是重叠区间的问题。本题是判断删掉多少个区间，能够得到不重合的区间组合。如下图：

第一步仍然是按照左边界排序，让所有区间按照大小顺序排在一起。

判断相邻两个区间不重叠，也就是i区间左边界>=i-1区间的右边界。

if(i>0&&nums[i][0]>nums[i-1][1]){continue;//不重叠直接继续遍历
}

判断区间如果重叠，那么计数+1（重叠的一定要删掉），和气球题目类似，依旧取最小右边界，看看下一个区间是否重叠

else{result++;//修改右边界nums[i][1]=min(nums[i][1],nums[i-1][1]);//修改后继续遍历即可
}

完整版

class Solution {
public:static bool cmp(vector<int>&a,vector<int>&b){if(a[0]<b[0])  return true;//左边界升序排序return false;}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if(intervals.size()==0) return 0;sort(intervals.begin(),intervals.end(),cmp);int count=0;for(int i=1;i<intervals.size();i++){if(intervals[i][0]>=intervals[i-1][1])  continue;//如果重叠，更新最小右边界else{count++;intervals[i][1]=min(intervals[i][1],intervals[i-1][1]);}}return count;}
};

注意点

在我们自己画图模拟重叠区间的时候，一定要注意，更新最小右边界之后，实际上重叠的区间相当于已经被修改了！也就是说，当前重叠区间的右边界，已经成为最小右边界了。

重叠区间原有右边界需要及时在图里删掉，否则容易出现看图看错逻辑的情况。模拟图如下图所示。

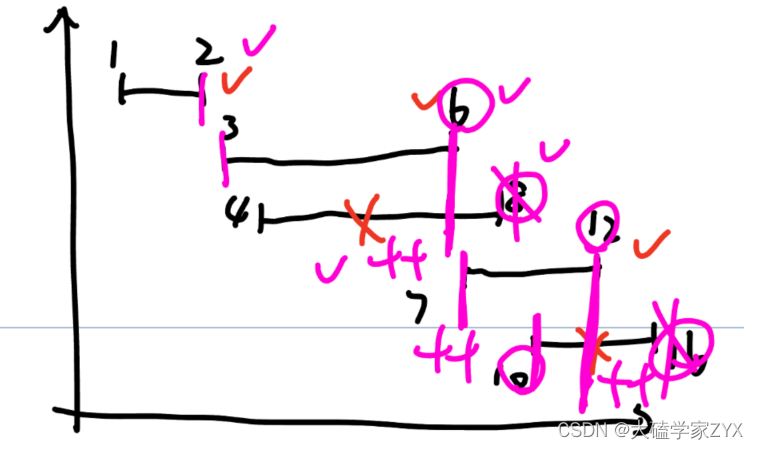
这种情况遍历到7的时候，实际上7前面和8重合的部分，8已经被删掉了，所以并不会出现i=3的重合。

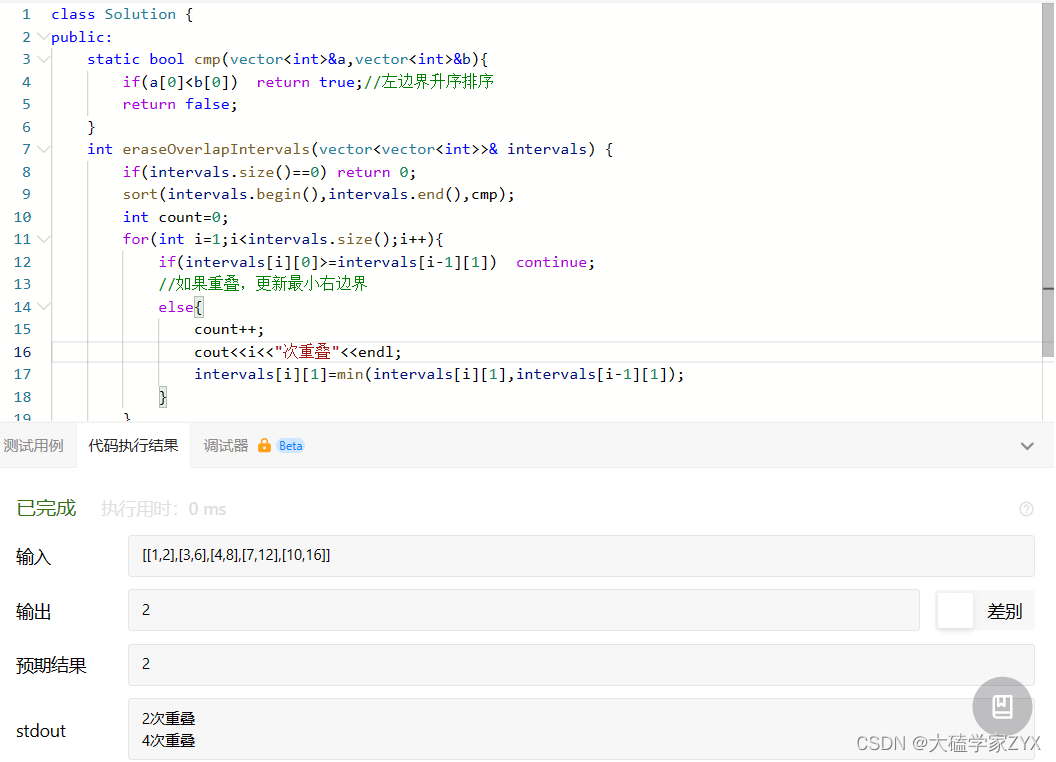
右区间排序

• 本题实际上改成右区间排序也能过，因为右区间其实找的还是重叠区间中的最小右区间，只修改cmp即可

class Solution {
public:static bool cmp(vector<int>&a,vector<int>&b){if(a[1]<b[1])  return true;//右边界升序排序return false;}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if(intervals.size()==0) return 0;sort(intervals.begin(),intervals.end(),cmp);int count=0;for(int i=1;i<intervals.size();i++){if(intervals[i][0]>=intervals[i-1][1])  continue;//如果重叠，更新最小右边界else{count++;intervals[i][1]=min(intervals[i][1],intervals[i-1][1]);}}return count;}
};

763.划分字母区间

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

示例 1：

输入：s = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的，因为划分的片段数较少。 

示例 2：

输入：s = "eccbbbbdec"
输出：[10]

提示：

• 1 <= s.length <= 500
• s 仅由小写英文字母组成

思路

本题首先要理解题意。题目中说同一字母最多出现在一个片段中，也就是说，对字母a来说，划分出来的片段应该包括所有的a。同时还要保证划分出来的片段数目是最多的。

也就是说，一旦包含a，就要包含所有的a，一旦包含b就要包含所有的b。

因此，本题的策略是找到每个元素的最远位置，然后看区间之间的包含关系。如下图所示：

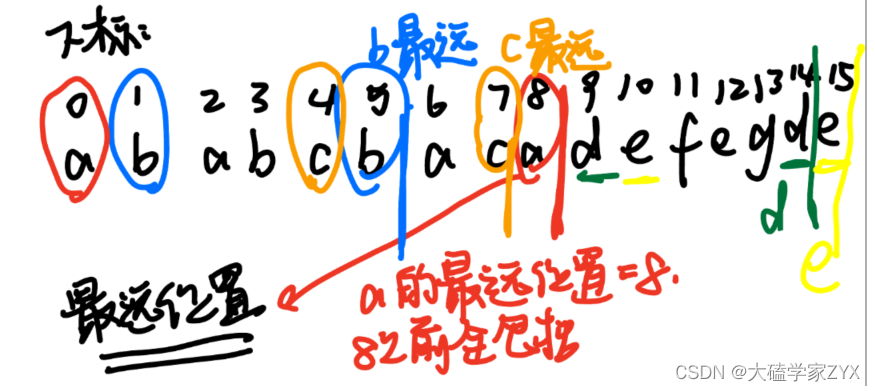
a的最远位置包含了b和c的最远位置。因此第一个区间的分界线就在a的最远位置处。d的最远位置没有包含e，因此我们最后的区间是de最远位置的最大值。

• 先确定每个元素的最远位置
• 根据最远位置确定区间分界线在哪里

完整版

• 记录最远出现位置，只需要hash[字母对应下标]=i就够了，因为出现位置就是是不断更新的i，比较近的下标都会被远处的下标覆盖。
• 我们用right=max(right,hash[s[i]-‘a’])的方式，来记录目前为止遍历到的所有元素的最远下标位置。一旦到了这个位置，说明目前为止所有元素的最远下标就是这里，可以计算长度结果了。
• 重置左区间起始点的时候注意，本题区间不能重合

class Solution {
public:vector<int> partitionLabels(string s) {vector<int>result;//次数数组int hash[27]={0};//先统计每个元素的最远位置for(int i=0;i<s.size();i++){hash[s[i]-'a']=i;//下标i不断更新，最后hash里面的i就是最远位置的i}int left=0,right=0;int length=0;//用right记录目前为止所有遍历元素的最大下标for(int i=0;i<s.size();i++){right = max(right,hash[s[i]-'a']);//如果已经到了最大下标if(i==right){cout<<right<<endl;cout<<left<<endl;length=right-left+1;result.push_back(length);left=right+1;//重置左区间起始点，注意这里一定要left+1，区间不能重合length=0;//重置长度}}return result;}
};

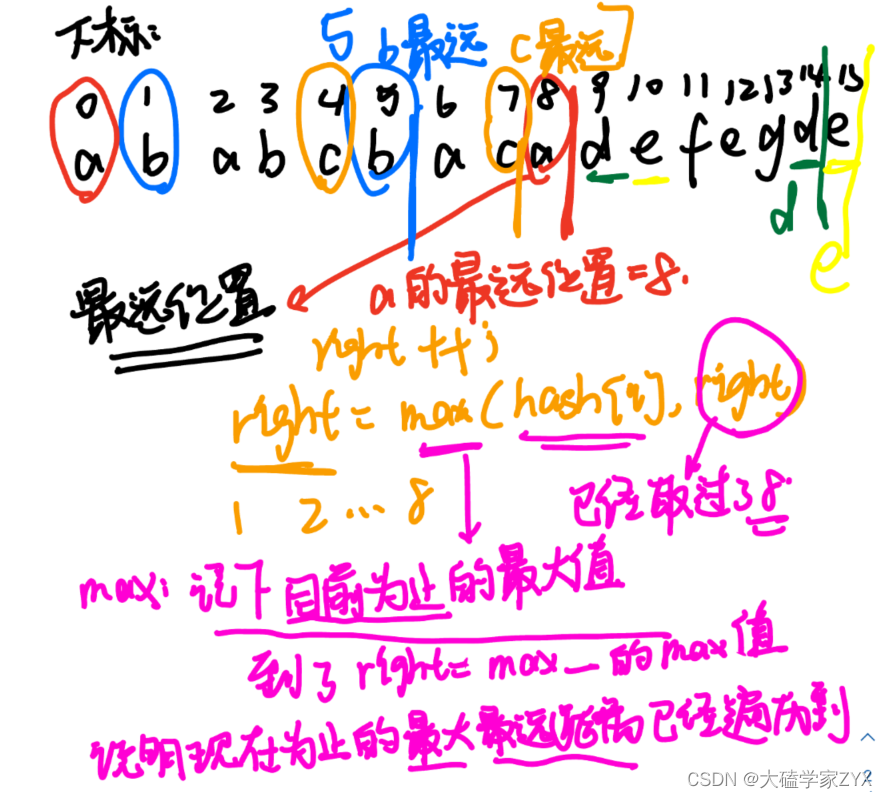
如何确定区间分界线

如下图所示，本题主要是利用max来记录目前为止遍历过的所有元素里，最远距离最大的那一个。

当right遍历到了max，也就是说，right目前在的位置，是目前遍历过的所有元素里，最远距离最大的元素！此时right的位置，就是区间的分界线！

debug测试

第一次提交出现了很奇怪的结果，因为left没赋初值，所以每一次运行，left的值都不一样。修改left=0后问题解决。

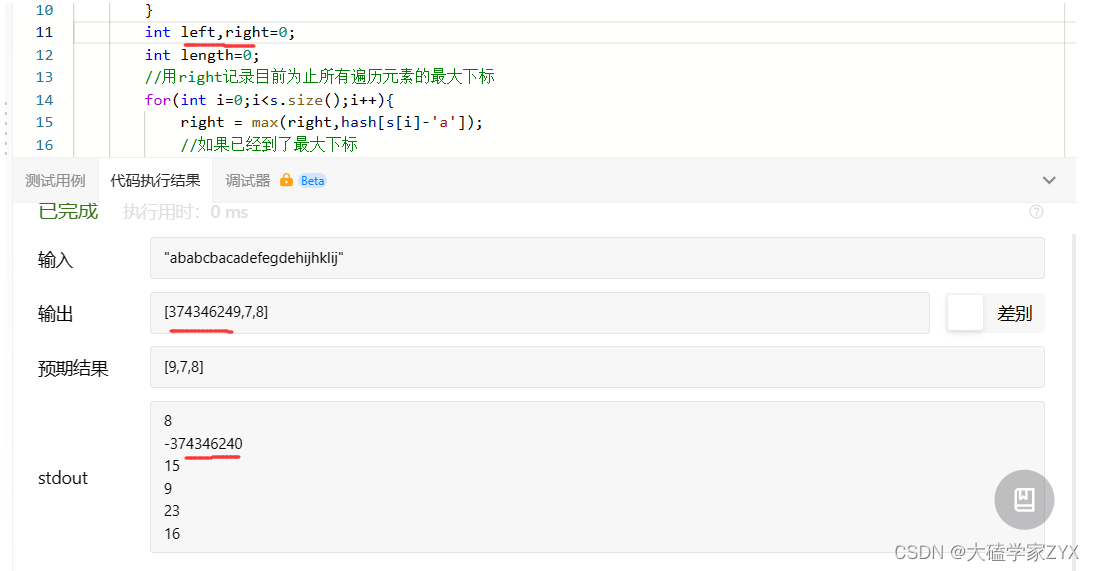
时间复杂度

• 时间复杂度：O(n)，两个并列的for是n+n，实际上结果还是O(n)
• 空间复杂度：O(1)，计数数组是固定大小

总结

这道题目leetcode标记为贪心算法，其实没有太体现贪心策略，找不出局部最优推出全局最优的过程。

本质上还是重叠区间的问题，就是用最远出现距离模拟了圈字符的行为。最远出现距离，相当于重叠区间中包含所有区间的最大区间。

56.合并区间（写法1比较考验思维，推荐写法2）

• 重叠区间题目需要注意元素初值的问题，包括计数变量的初值，以及有时候需要考虑数组i=0时候的初值（因为重叠判断大都是i=1开始的）

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

提示：

• 1 <= intervals.length <= 10^4
• intervals[i].length == 2
• 0 <= starti <= endi <= 10^4

思路

本题是重叠区间经典题目，和 452.最少弓箭引爆气球 435.无重叠区间 的思路非常类似。

但是也有不同的地方，这道题如果完全按照无重叠区间思路来做，会有逻辑问题，本题因为是result数组收集合并后的区间，因此我们需要更新的是result的最后一个元素，而不是直接在原数组上修改，遇到重叠区间取最值加入result。

写法1：直接在原数组上修改，更新i-1

• 这种写法和更新result.back()很像，但是逻辑是错误的，原因是更新i-1再把i-1加入数组的话，遍历到i+1的时候，i+1并没有接收到i-1更新的信息！

class Solution {
public://原数组上直接合并的写法static bool cmp(vector<int>&a,vector<int>&b){if(a[0]<b[0]) return true;//左边界升序排序return false;}vector<vector<int>>result;vector<vector<int>> merge(vector<vector<int>>& intervals) {sort(intervals.begin(),intervals.end(),cmp); for(int i=1;i<intervals.size();i++){//完全不重叠if(intervals[i][0]>intervals[i-1][1]){//cout<<intervals[i-1][1]<<" "<<intervals[i][0]<<endl;//把i-1放进去，而不是iresult.push_back(intervals[i-1]);continue;}//<=都算重叠if(intervals[i][0]<=intervals[i-1][1]){//左边界已经排好序了不用管了//intervals[i-1][0]=min(intervals[i-1][0],intervals[i][0]);//更新i-1右边界intervals[i-1][1]=max(intervals[i-1][1],intervals[i][1]);result.push_back(intervals[i-1]);}//最后一个单独判断，如果不重叠加入自身if(i==intervals.size()-1&&intervals[i][0]>intervals[i-1][1])result.push_back(intervals[i]);}return result;}
};

debug测试

这种写法出现了逻辑错误，因为我们从i=1开始遍历，i=1时更新了i-1为新数组，但是遍历到i=2的时候，并没有接收到新数组的信息，而是依然在和i对比！

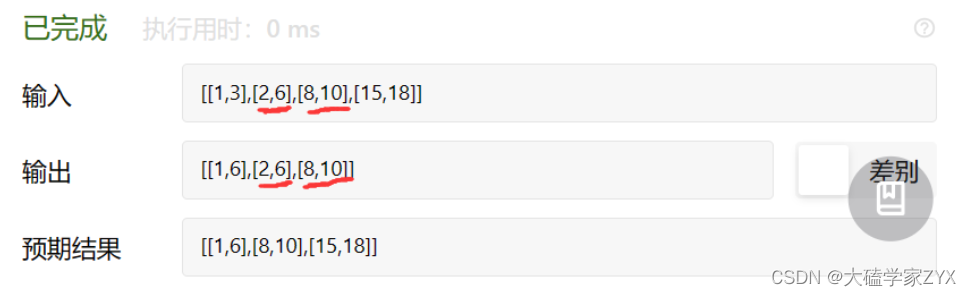
写法1修改版

• 这种写法比较考验思维，核心在于重叠的时候更新i而不是i-1从而能让下一个元素接收到更新信息。还是推荐第二种写法
• 最后一个元素，可以直接放入结果数组，是因为不重叠显然可以直接放，即使重叠也是修改完了当前的i，所以也可以直接push_back()。

class Solution {
public://原数组上直接合并的写法static bool cmp(vector<int>&a,vector<int>&b){if(a[0]<b[0]) return true;//左边界升序排序return false;}vector<vector<int>>result;vector<vector<int>> merge(vector<vector<int>>& intervals) {sort(intervals.begin(),intervals.end(),cmp); for(int i=1;i<intervals.size();i++){//完全不重叠if(intervals[i][0]>intervals[i-1][1]){//cout<<intervals[i-1][1]<<" "<<intervals[i][0]<<endl;//把i-1放进去，而不是iresult.push_back(intervals[i-1]);continue;}//<=都算重叠if(intervals[i][0]<=intervals[i-1][1]){//更新i而不是i-1intervals[i][0]=min(intervals[i-1][0],intervals[i][0]);//更新i右边界intervals[i][1]=max(intervals[i-1][1],intervals[i][1]);//更新之后直接遍历下一个即可，下一个发现不重叠会直接加入结果集}}//所有都结束之后再push_backresult.push_back(intervals[intervals.size()-1]);return result;}
};

(推荐)写法2：更新result.back()

• 由于本题是result存放结果，因此我们可以直接在结果数组中进行判断，这样就包含了第一个元素值的逻辑
• 注意result.back()[1]就是上个元素的右边界！

class Solution {
public:static bool cmp(vector<int>&a,vector<int>&b){if(a[0]<b[0]) return true;//左边界升序排序return false;}vector<vector<int>>result;vector<vector<int>> merge(vector<vector<int>>& intervals) {sort(intervals.begin(),intervals.end(),cmp);//先把第一个元素加进去result.push_back(intervals[0]);//开始遍历for(int i=1;i<intervals.size();i++){//完全不重叠,直接和.back()比较if(result.back()[1]<intervals[i][0]){result.push_back(intervals[i]);}else{//更新上个元素的右边界,左边界已经排好序了//这里需要取最大值，和他本身作比较result.back()[1]=max(intervals[i][1],result.back()[1]);}}return result;}
};

时间复杂度

• 时间复杂度: O(nlogn)
• 空间复杂度: O(n)，结果数组大小

1. 时间复杂度：代码中的排序操作是时间复杂度最高的部分。在C++中，std::sort的平均时间复杂度为O(N log N)，其中N是intervals的长度。其余的操作，包括遍历和比较，时间复杂度为O(N)。因此，总的时间复杂度是O(N log N + N)，但是在大O表示法中，我们通常只关心最高阶项，所以我们可以忽略掉O(N)部分，所以总的时间复杂度是O(N log N)。
2. 空间复杂度：代码中的空间复杂度主要取决于结果result的大小。在最坏的情况下，如果所有的区间都不重叠，那么result的大小和输入的intervals大小相同，即N。除此之外，sort操作使用的是原地排序，不需要额外的存储空间。所以总的空间复杂度是O(N)。

总结

关于重叠区间类型的题目，其实主要就是靠画图模拟。

重叠区间题目需要注意元素初值的问题，包括计数变量的初值，以及有时候需要考虑数组i=0时候的初值（因为重叠判断大都是i=1开始的）。

比如本题，是结果收集而不是记录重叠个数，此时就需要考虑数组初值也要被加入结果数组的情况！