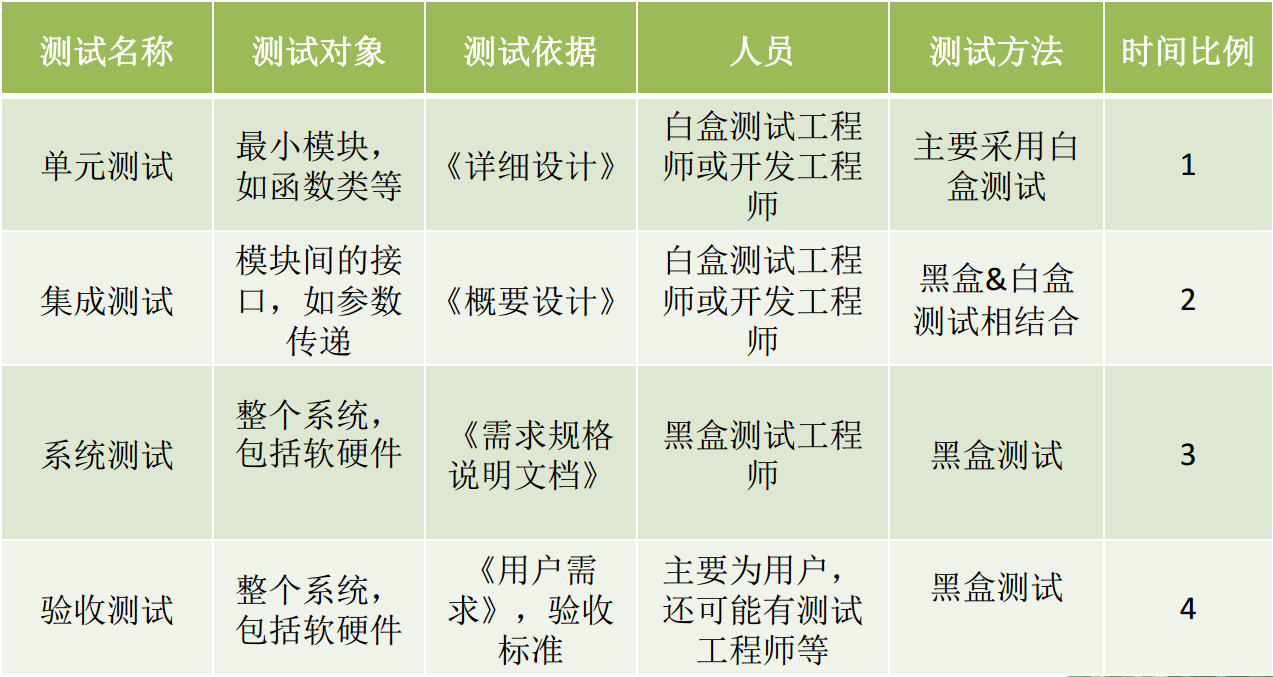
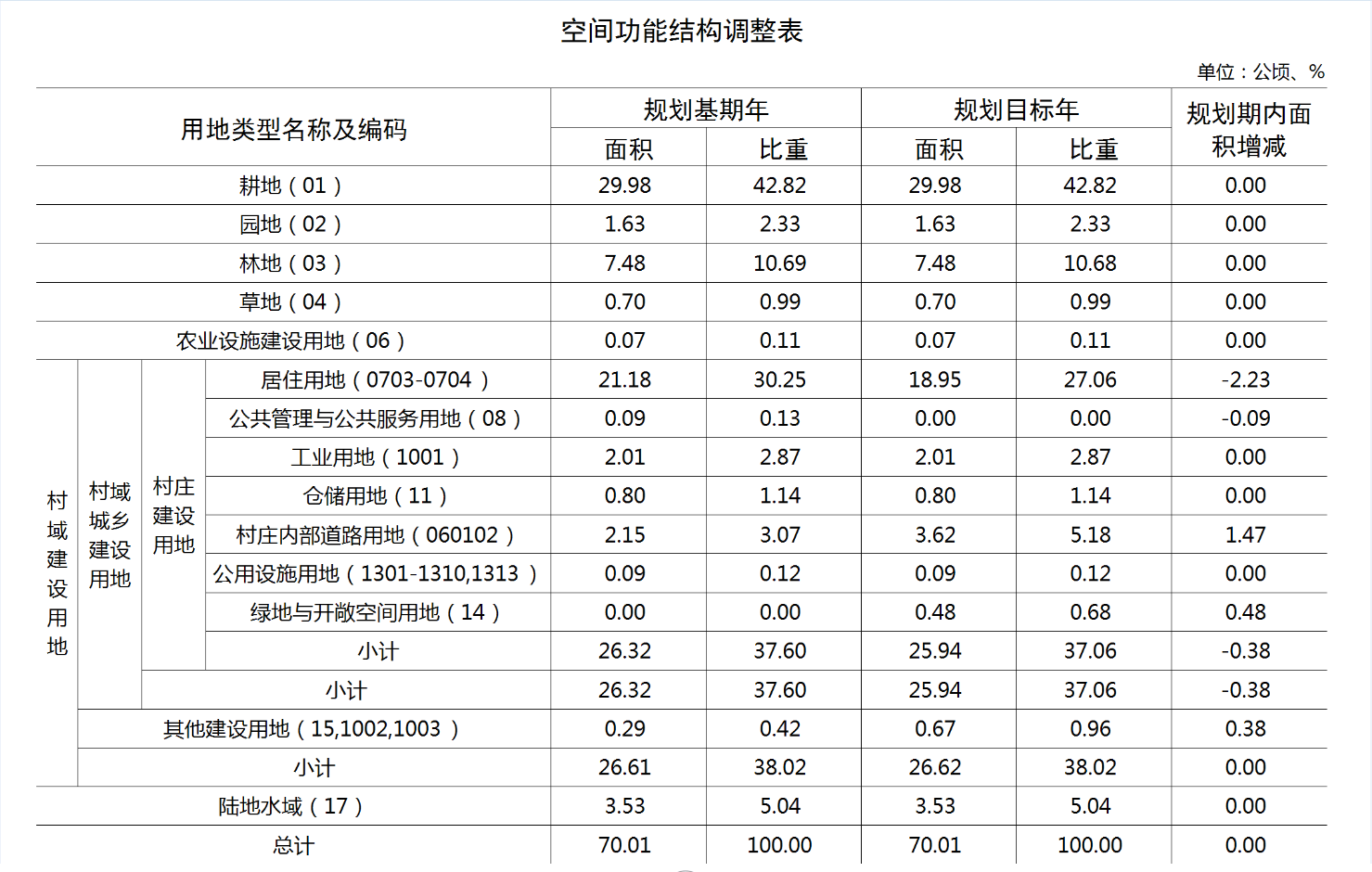
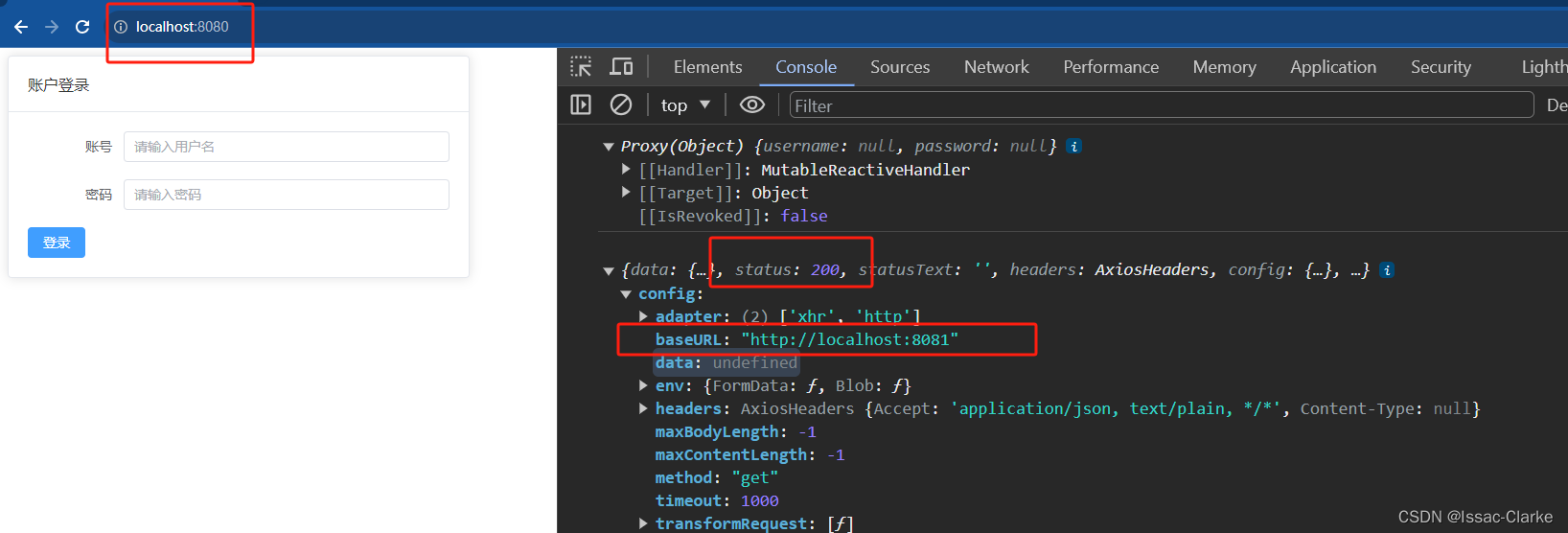
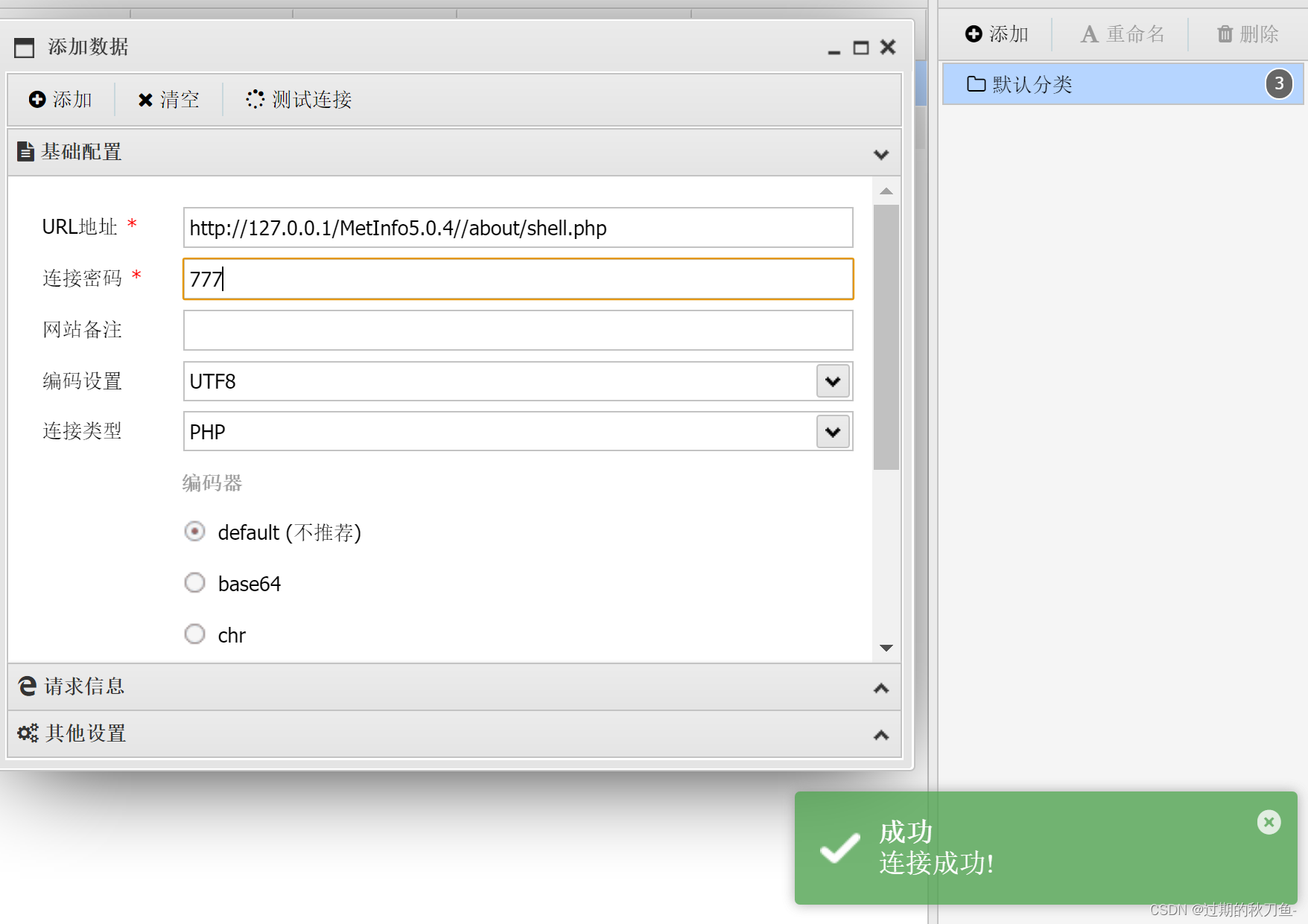
个人对IMU的漂移一直以来都很困惑,总结整理了这些材料,希望能理清楚一点思路。
总的来讲,IMU的漂移可建模为三部分,随机常值+相关漂移+白噪声,
但实际使用时,三者都出现的用法很少。严恭敏老师在博客中有相关的讨论https://zhuanlan.zhihu.com/p/556696975
博客中指出,在秦永元老师《卡尔曼滤波与组合导航原理》一书8.4.3节“惯导系统的误差源模型”也有相关论述。因其全面,现以此为主要内容讨论。
对于陀螺仪的随机漂移,可分为三种:



综合以上两种材料,总结来看,上述漂移的三个部分,白噪声不被列入卡尔曼滤波状态量,可以不用单独考虑。主要的变数是在相关漂移那一项。
1)最简单的是相关时间很短,相关漂移可视为白噪声,建模为随机常值bias+测量白噪声(积分后导致角度随机游走)。测量白噪声的方差阵可由allan方差中的角度随机游走系数给出。
2)其次是建模为一阶马尔科夫过程+测量白噪声,这种情况适用于相关时间很长,且超过了惯导工作时间,将随机常值+相关漂移等效为一个新的相关漂移(形式上还是一阶马尔科夫过程)。此时,一阶马尔科夫过程的驱动噪声的方差,由allan方差中的零偏不稳定性通过下面公式计算得到

在上图中,可将零偏不稳定性为Rx(0),将其乘上2beta(相关时间的倒数),即为(连续时间)等效激励噪声的方差阵。后面将q离散化可得到等效离散化噪声方差阵Qk。
3)还有一种情况比较多见,就是将相关分量等效为随机游走过程(bias项的一阶导为白噪声),整体漂移则为随机游走+测量白噪声,这在vslam领域多见(一些vslam的书、开源项目都是如此)。而有关INS及组合导航的文献,sola的《Quaternion kinematics for the error-state Kalman filter》中也是这么定义的。
在秦老师的分析中,这种情况属于相关时间比较长的情况。但对随机游走的驱动噪声方差如何求取的过程没有看懂。
在imu-camera标定开源工具kalibr中,imu建模就是这种情况,它是选择了allan方差中的角速率随机游走系数来表征随机游走驱动白噪声标准差连续形式)。