题目链接

NOIP2005提高组第二轮T3：传纸条

题目描述

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排坐成一个 $m$ 行 $n$ 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 $(1,1)$，小轩坐在矩阵的右下角，坐标 $(m,n)$。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 $0$ 表示），可以用一个 $[0,100]$ 内的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。现在，请你帮助小渊和小轩找到这样的两条路径。

输入格式

第一行有两个用空格隔开的整数 $m$ 和 $n$，表示班里有 $m$ 行 $n$ 列。

接下来的 $m$ 行是一个 $m\times n$ 的矩阵，矩阵中第 $i$ 行 $j$ 列的整数表示坐在第 $i$ 行 $j$ 列的学生的好心程度。每行的 $n$ 个整数之间用空格隔开。

输出格式

输出文件共一行一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

样例 #1

样例输入 #1

3 3
0 3 9
2 8 5
5 7 0

样例输出 #1

34

提示

【数据范围】

对于 $30\%$ 的数据，满足 $1\le m,n\le 10$。
对于 $100\%$ 的数据，满足 $1\le m,n\le 50$。

算法思想（动态规划）

根据题目描述，要求从$(1,1)$到$(n,m)$、然后再从$(n,m)$到$(1,1)$，来回两条路上参与传递纸条的学生的好心程度之和的最大值。

首先，从右下角$(n,m)$回传其实可以等价为从左上角$(1,1)$再传一次，这样就变为从左上角同时传两次（选择两条路径）到达右下角。

考虑到班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说这两条路径不能存在交点。那么这两条路径会不会存在交点呢？

如果两条路径存在这样的交点：

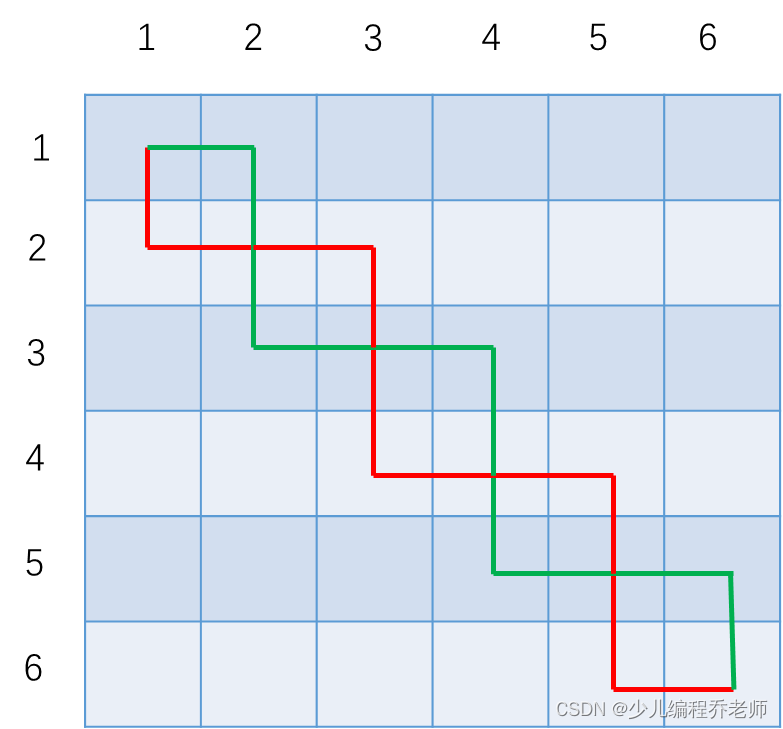
那么只要把位于红色下方的绿线段，与和它呈对称的红色线段交换一下，此时就可以得到：

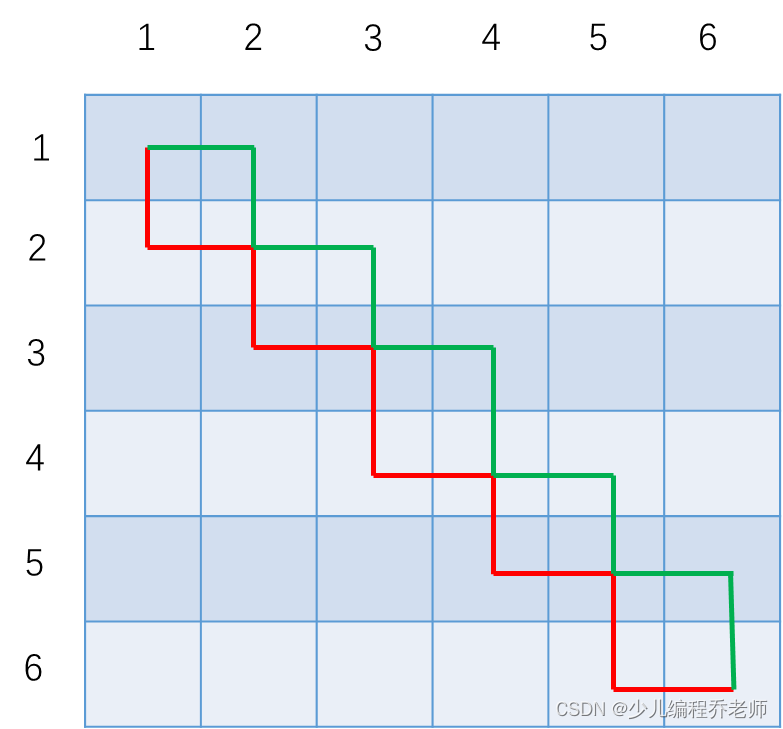
由于这两条路径经过的同学是一样的，因此交换之后是等价的，但是两条路径仍旧存在交点。此时，如果选择将红色的路径“绕一下路”（如下图虚线部分所示），由于会多经过一名同学，那么得到的答案不会劣于之前的路径。当然也可能是将绿色的路径“绕一下路”，这个选择取决于走哪个路径收益更大。

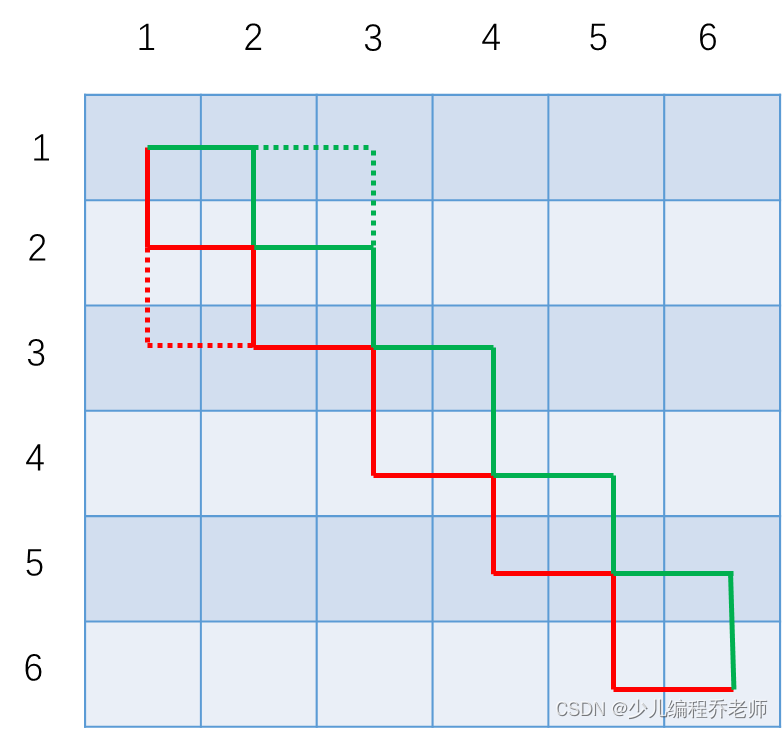
因此可以得到结论，绕过交点得到的收益一定不会比存在交点的方案更差。因此，可以认为最优解的路径方案中不存在交点。

有了上述性质，就可以让两个纸条同时从起点出发，每次同时走一步，由于只能向下和向右走，最终会同时到达右下角。那么可以用下述动态规划思想来解决：

• 状态表示：f[k,x1,x2]表示两个纸条同时走了k步之后，第一个纸条到达(x1, k-x1)、第二个纸条到达(x2, k-x2)时的最大值。
• 状态计算，可以按照最后一步两个人的走法分成下面$4$种情况，取其中的最大值：
  • 两个纸条同时向右走，为f[k - 1, x1, x2] + w[k, x1, x2]
  • 两个纸条第一个向右走、第二个向下走，为f[k - 1, x1, x2-1] + w[k, x1, x2]
  • 两个纸条第一个向下走、第二个向右走，为f[k - 1, x1-1, x2] + w[k, x1, x2]
  • 两个纸条同时向下走，为f[k - 1, x1-1, x2-1] + w[k, x1, x2]

需要注意的是，在状态计算中：

• 两个人不能走到相同格子，即x1和x2不能相等
• w[k,x1,x2]表示的是格子(x1,k-x1)和(x2,k-x2)的好心程度之和

时间复杂度

一共有 $O(n^3)$ 个状态，每个状态需要 $O(1)$的计算量，因此总时间复杂度是 $O(n^3)$。

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100;
int w[N][N], f[2 * N][N][N];
int main()
{//n行m列int n, m;cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)cin >> w[i][j];//枚举步数k，从2开始，起点的好心程度为0for(int k = 2; k <= n + m; k ++)for(int x1 = 1; x1 <= n; x1 ++) //枚举行for(int x2 = 1; x2 <= n; x2 ++){//计算到达的列int y1 = k - x1, y2 = k - x2;//越界检查if(y1 < 1 || y1 > m || y2 < 1 || y2 > m) continue;int t = w[x1][y1];//如果不是同一个位置if(x1 != x2) t += w[x2][y2];//状态计算，按照最后一步两个人的走法取4种情况的最大值f[k][x1][x2] = max(f[k][x1][x2], f[k - 1][x1][x2] + t);f[k][x1][x2] = max(f[k][x1][x2], f[k - 1][x1][x2 - 1] + t);f[k][x1][x2] = max(f[k][x1][x2], f[k - 1][x1 - 1][x2] + t);f[k][x1][x2] = max(f[k][x1][x2], f[k - 1][x1 - 1][x2 - 1] + t);}//最终结果是两个纸条同时走到第n行的状态cout << f[n + m][n][n]; return 0;        
}