CentOS7查看和关闭防火墙

1.CentOS 7 默认使用的是firewall作为防火墙

2.查看防火墙状态

# 方法1
systemctl status firewalld# 方法2
firewall-cmd --state

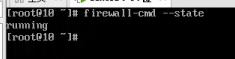
3.停止firewall

systemctl stop firewalld.service

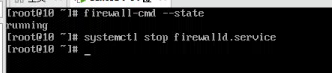
4.禁止firewall开机启动

systemctl disable firewalld.service 

5.开启防火墙开机启动

systemctl enable firewalld.service

6.开启端口

#注：可以是一个端口范围，如1000-2000/tcp
firewall-cmd --zone=public --add-port=80/tcp --permanent

7.移除端口

# 方法1
firewall-cmd --zone=public --remove-port=80/tcp --permanent
# 方法2
firewall-cmd --permanent --remove-port=123/tcp

8.重启防火墙

firewall-cmd --reload

9.查看某个端口是否开启

firewall-cmd --query-port=80/tcp

10.查询开放列表

firewall-cmd --list-port

总结:systemctl常用命令

systemctl是CentOS7的服务管理工具中主要的工具，它融合之前service和chkconfig的功能于一体。# 启动一个服务：
systemctl start firewalld.service
# 关闭一个服务：
systemctl stop firewalld.service
# 重启一个服务：
systemctl restart firewalld.service
# 显示一个服务的状态：
systemctl status firewalld.service
# 在开机时启用一个服务：
systemctl enable firewalld.service
# 在开机时禁用一个服务：
systemctl disable firewalld.service
# 查看服务是否开机启动：
systemctl is-enabled firewalld.service
# 查看已启动的服务列表：
systemctl list-unit-files|grep enabled
# 查看启动失败的服务列表：
systemctl --failed

总结:firewalld-cmd配置

# 查看版本：
firewall-cmd --version
# 查看帮助： 
firewall-cmd --help
# 显示状态： 
firewall-cmd --state
# 查看所有打开的端口： 
firewall-cmd --zone=public --list-ports
# 更新防火墙规则： 
firewall-cmd --reload
# 查看区域信息:  
firewall-cmd --get-active-zones
# 查看指定接口所属区域： 
firewall-cmd --get-zone-of-interface=eth0
# 拒绝所有包：
firewall-cmd --panic-on
# 取消拒绝状态：
firewall-cmd --panic-off
# 查看是否拒绝：
firewall-cmd --query-panic