前言
在今天的题目开始之前,让我们来回顾一下之前的知识,动规五部曲
1.确定dp数组含义
2.确定dp数组的递推公式
3.初始化dp数组
4.确定遍历顺序
5.打印dp数组来排错
tips: 1.当求取物品有限的时候用0-1背包,求取物品无限的时候用完全背包
结果是排列还是组合也有说法,当结果是组合的时候,遍历顺序为先物品,后背包,保证无序性
如果先遍历背包,后遍历物品,这个时候求的就是排列数
LeetCode T70 爬楼梯
题目链接:70. 爬楼梯 - 力扣(LeetCode)

题目思路:
相信之前看过我文章的友友们应该不陌生这道题,我们之前是使用斐波那契数列的方式来推导递推公式进行操作的,现在我们不妨换个思路,把他想成一个完全背包的问题进行解决,这里我们的背包容量就是n,可选物品就是1和2,我们仍然使用动规五部曲来分析一下.
1.确定dp数组含义
这里的dp数组含义就是装满容量为n的背包的方法数
2.确定dp数组的递推公式
和前面的一样累加即可
dp += dp[j-i] 因为这里价值就是其本身
3.初始化dp数组
这里全部初始化为0即可
4.确定遍历顺序
这里是求排列问题,所以使用先背包后物品来操作
记得遍历物品的时候要从前向后,判断一下i是否大于j在做累加
5.打印dp数组来排错
题目代码:
class Solution {public int climbStairs(int n) {int[] dp = new int[n+1];dp[0] = 1;for(int i = 1;i<=n;i++){for(int j = 1;j<=2;j++){if(i>=j){dp[i] += dp[i-j];}}}return dp[n];}
}LeetCode T322 零钱兑换
题目链接:322. 零钱兑换 - 力扣(LeetCode)

题目思路:
这题仍然是一个完全背包的问题,不过这里我们要求的是装满背包的最少物品数,这里我们就不能考虑初始化为0了,我们得初始化为一个较大的数,才能够方便我们来覆盖掉之前的数组值
我们下面仍然用动规五部曲来安排一下这道题
1.确定dp数组含义
这里dp[j]的含义就是j容量的数组最小能由几个物品装满
2.确定dp数组的递推公式
dp[j] = Math.min(dp[j],dp[j-coins[i]]+1);
3.初始化dp数组
这里得初始化为int的最大值,有人可能直接一股脑就初始化为0了,那么仔细想想,这样求最小值一直都会是0,只有数足够大才能让小值能覆盖数组中的对应元素
记得dp[0]得赋值为0,不然也操作不了,假设dp[0]没有赋值为0那么后面的int最大值再+1就会越界.
4.确定遍历顺序
先遍历物品,再遍历背包即可
5.打印dp数组来排错
题目代码:
class Solution {public int coinChange(int[] coins, int amount) {int[] dp = new int[amount+1];Arrays.fill(dp,Integer.MAX_VALUE);dp[0] = 0;for (int i = 0; i < coins.length; i++) {//正序遍历:完全背包每个硬币可以选择多次for (int j = coins[i]; j <= amount; j++) {//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要if (dp[j - coins[i]] != Integer.MAX_VALUE) {//选择硬币数目最小的情况dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}if(dp[amount]==Integer.MAX_VALUE){return -1;}else{return dp[amount];}}
}LeetCode T279 完全平方数
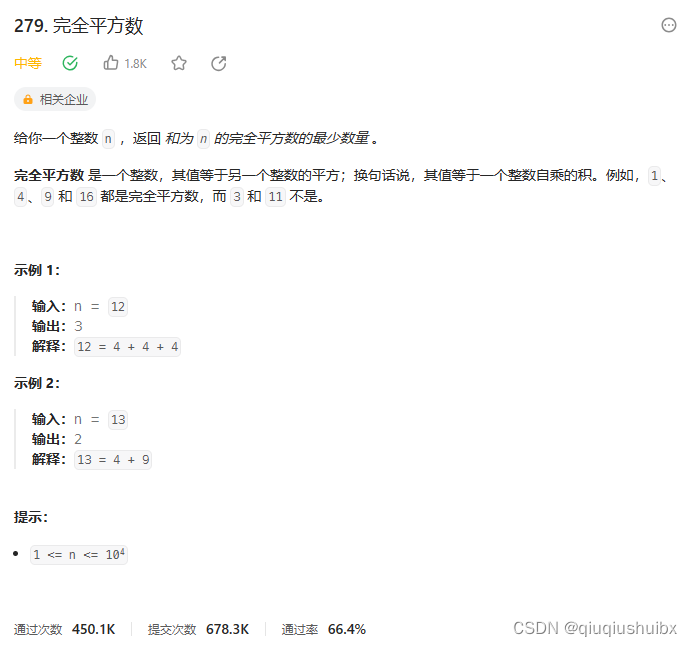
题目链接:279. 完全平方数 - 力扣(LeetCode)
题目思路:
只要上题能搞得明白,这题完全没有难度,首先只需要得到小于等于n的所有平方数,来填满这个容量为n的背包,求其最少能装满的即可.下面我们仍然是使用动规五部曲去玩一下.
1.确定dp数组含义
dp[j]:装满背包容量为j的背包最少需要多少平方数
2.确定dp数组的递推公式
和之前一样,dp[j] = Math.min(dp[j],dp[j-i*i]+1);这里的价值为i*i
3.初始化dp数组
dp[0]初始化为0,其他的初始化为Integer.MAX_VALUE即可
4.确定遍历顺序
先背包后数组即可,因为不涉及遍历顺序,所以都行
5.打印dp数组来排错
题目代码:
class Solution {public int numSquares(int n) {int[] dp = new int[n+1];Arrays.fill(dp,Integer.MAX_VALUE);dp[0] = 0;for(int i = 1;i*i<=n;i++){for(int j = i*i;j<=n;j++){dp[j] = Math.min(dp[j],dp[j-i*i]+1);}}return dp[n];}
}