给定n个点或一个凸边形，求其最小外接矩形，可视化-编程知识

给定n个点或一个凸边形，求其最小外接矩形，可视化

这里写目录标题

原理
代码

原理

求n个点的最小外接矩形问题可以等价为先求这n个点的凸包，再求这个凸包的最小外接矩形。

其中求凸包可以使用Graham-Scan算法
需要注意的是，
因为Graham-Scan算法要求我们从先找到凸包上的一个点，所以我们可以先对这些点进行排序，根据x/y坐标都可以。排序后的第一个点和最后一点一定在凸包上。
同时，假设我们按照x排序，并且想要得到顺时针旋转的凸包边界，那么我们只能找到一半的边界，这是因为我们从左到右遍历这些点的时候只有上面的点才满足顺时针，下面的不可能满足顺时针(这里为了节省计算可以只对y坐标大于开始和结束点中最小y坐标的点进行计算)。
为了找到全部的点，我们需要正向判断完后再反向相同方法判断一遍。
这里为了判断是顺时针还是逆时针，我们使用的是两个方向叉乘的最后一项，从前一个方向转到后一个方向时：如果叉乘最后一项小于0，说明是顺时针旋转的（右手系）。
给定一个凸多边形，求最小外接矩形的原理可以参考这篇博客https://blog.csdn.net/wang_heng199/article/details/74477738
简单而言就是对凸包上的每条边构造矩形并比较面积。
我们这里的做法是遍历每条边，对于每条边，我们根据它与水平方向的夹角计算其旋转矩阵，并将这些凸包上的所有点根据此旋转矩阵的逆矩阵/转置矩阵(旋转矩阵是正交矩阵)旋转至水平方向，此时我们可以很容易得到这些点水平方向和竖直方向的边界点，从而就有了一个外接矩形。

代码

导入包并且初始化随机点：

import numpy as np
import matplotlib.pyplot as plt
n = 100
points = np.random.randn(n, 2)

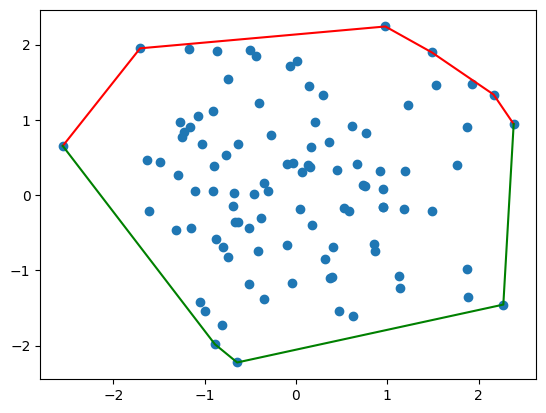
计算凸包并可视化

sorted_points = points[np.argsort(points[:,0])]def cal_rotate_orientation(cur,stack_end,stack_end_before):'''计算p1->p2的向量旋转到p2->p3的向量是顺时针还是逆时针'''p1,p2,p3 = sorted_points[stack_end_before], sorted_points[stack_end], sorted_points[cur]x2,y2 = p3 - p2x1,y1 = p2 - p1return x1*y2 - x2*y1    #叉乘最后一项Z轴方向，<0:顺时针，>0:逆时针def cal_convex_hull(index_list):result = list(index_list[:2])index_list = index_list[2:]for i in index_list:if (cal_rotate_orientation(i,result[-1],result[-2]) < 0):  #叉乘最后一项 ，符合顺时针# print(i,result[-1],result[-2])result.append(i)else:if len(result) == 2: result[-1] = i   continueresult.pop()while(cal_rotate_orientation(i,result[-1],result[-2]) > 0):   #不是顺时针，需要反复剔除result.pop()if len(result) < 2:breakresult.append(i)return result#n-1是最后一个点，因为它肯定在第一遍的结果里，所以两个结果合并时去除第一个
result = cal_convex_hull(range(0,n,1))+cal_convex_hull(range(n-1,-1,-1))[1:]
print(result)
#ploy是将结果按照顺序两两组合，形成边界
ploy = list(map(lambda i:result[i:i+2],range(0,len(result)-1)))plt.scatter(sorted_points[:, 0], sorted_points[:, 1])
plt.plot(sorted_points[result,0],sorted_points[result,1],color = 'red')
plt.show()

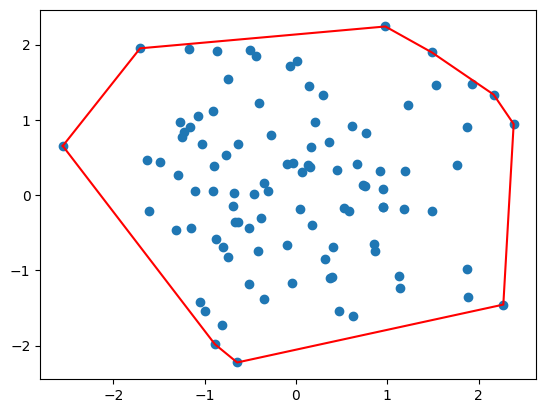
在这里插入图片描述

计算最小外接矩形
这里为了可视化，我们会将矩形转回来。

def get_rotate(cos,sin):#我们已知在原坐标系下的方向，要将其转化到目标系，用逆/转置return np.array([[cos,-sin],[sin,cos]])   def get_rotate2(theta):#我们已知在原坐标系下的方向，要将其转化到目标系，用逆/转置return np.array([[np.cos(theta),-np.sin(theta)],[np.sin(theta),np.cos(theta)]])row = 3
col = (len(ploy)+1)//3+1
fig, axs = plt.subplots(row, col, figsize=(15, 15))min_rect = [[],0,np.inf] #rect,angle,area
#假设是-90度 -> 90度
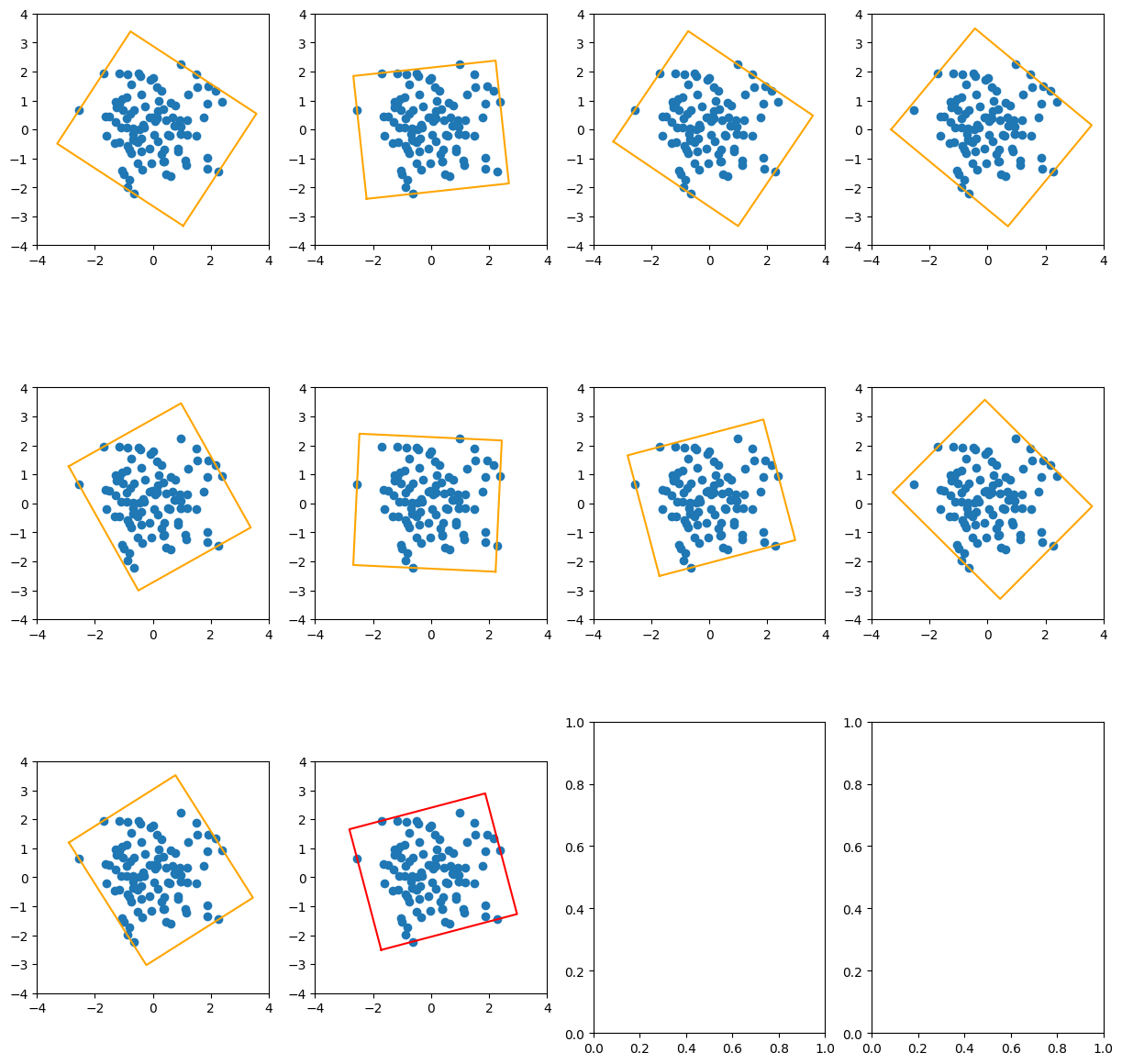
for idx, (i,j) in enumerate(ploy):x1,y1 = sorted_points[i]x2,y2 = sorted_points[j]tan_theta = (y2-y1)/(x2-x1)cos_theta = np.sqrt(1/(1+np.power(tan_theta,2)))sin_theta = cos_theta*tan_thetarotated_points = sorted_points@get_rotate(cos_theta,sin_theta)min_x,min_y = np.min(rotated_points,axis=0)max_x,max_y = np.max(rotated_points,axis=0)rect_xy = np.array([[min_x,min_y],[max_x,min_y],[max_x,max_y],[min_x,max_y]])rect_area = (max_x-min_x)*(max_y-min_y)if rect_area < min_rect[2]:min_rect = [rect_xy,np.arcsin(-sin_theta),rect_area]  #这个角度是取反，因为要转回去rect_xy = rect_xy@get_rotate(cos_theta,-sin_theta)  #转一下axs[idx//col,idx%col].scatter(points[:, 0], points[:, 1])plot_idx = [i for i in range(0,4)]+[0]axs[idx//col,idx%col].plot(rect_xy[plot_idx,0],rect_xy[plot_idx,1],color = 'orange')axs[idx//col,idx%col].set_xlim(-4,4)axs[idx//col,idx%col].set_ylim(-4,4)axs[idx//col,idx%col].set_aspect('equal')rect_xy = min_rect[0]@get_rotate2(min_rect[1])axs[(idx+1)//col,(idx+1)%col].scatter(points[:, 0], points[:, 1])
plot_idx = [i for i in range(0,4)]+[0]
axs[(idx+1)//col,(idx+1)%col].plot(rect_xy[plot_idx,0],rect_xy[plot_idx,1],color = 'red')
axs[(idx+1)//col,(idx+1)%col].set_xlim(-4,4)
axs[(idx+1)//col,(idx+1)%col].set_ylim(-4,4)
axs[(idx+1)//col,(idx+1)%col].set_aspect('equal')
plt.show()