from time import time
from bisect import bisect
from random import choices, seed
from itertools import combinationsdef func1(seq):# 暴力穷举,从最长的子序列开始查找,大约耗时5小时for n in range(len(seq)-1, 0, -1): # 依次查找长度为len(seq-1),len(sqe-1)-1,....3,2,1for sub in combinations(seq,n): # 枚举出seq中所有的长度为n的序列,元素原来的先后顺序不变if list(sub) == sorted(sub):return sub # 因为是从最长向最短判断的,产生返回的肯定是长度最长的def func2(seq):# 获取可能的最大长度,缩小后面循环的范围,大约耗时1小时# 比fun1的优点是先判断出最大可能长度m = 0for i in range(len(seq)-1):if seq[i+1]>seq[i]:m = m+1if seq[-1] > seq[-2]:m = m+1for n in range(m+1, 0, -1):for sub in combinations(seq, n): if list(sub) == sorted(sub):return subdef func3(seq):# 查找最长非递减子序列的长度,直接确定后面组合时的长度,4秒# 动态规划法,查表length = [1]*len(seq)for index1, value1 in enumerate(seq): # 如果前面有更小的元素,就更新当前元素为终点的子序列长度for index2 in range(index1):if seq[index2] <= value1: # 存在前面数小于本轮待比较数length[index1] = max(length[index1], length[index2]+1) # 迭代是从0开始的,length最小的序号会最先确定长度m = max(length)for sub in combinations(seq, m):if list(sub) == sorted(sub):return subdef func4(seq):# 查找最长非递减子序列的长度,直接确定后面组合时的长度,3.66秒# 比func3的优点时,先排除掉无效子序列,减少第2步比较数量length = [1]*len(seq)for index1, value1 in enumerate(seq):for index2 in range(index1):if seq[index2] <= value1:length[index1] = max(length[index1], length[index2]+1)m = max(length)for sub in combinations(seq, m):# 测试每个子序列中是否有违反顺序的相邻元素,避免对整个子序列排序for i,v in enumerate(sub[:-1]):if sub[i] > sub[i+1]:breakelse:return subdef func5(seq):# 查找最长非递减子序列的长度,直接确定后面组合时的长度,3.7秒# [7,1,2,5,3,4,0,6,2]# sub = [1,2,3,4,6]# sub = [7]# sub = [1]# sub = [1,2,5]# sub = [1,2,3]# sub = [1,2,3,4]# sub = [0,2,3,4]# sub = [0,2,3,4,6]# sub = [0,2,3,4,6]sub = []m = 0# 循环结束后,m为最大非递减序列的长度,但sub并不是要求的子序列for value in seq:index = bisect(sub, value) # 使用bisect,要求sub必须为有序排列if index == m:sub.append(value)m = m + 1else:sub[index] = valuefor sub in combinations(seq, m):# 测试每个子序列中是否有违反顺序的相邻元素,避免对整个子序列排序for i,v in enumerate(sub[:-1]):if sub[i] > sub[i+1]:breakelse:return subdef func6(seq):# 空间换时间,用来存放当前元素为终点的非递减子序列(暂未理解)sub = [[num] for num in seq]for index1, value1 in enumerate(seq[1:], start=1):for index2 in range(index1):if seq[index2] <= value1:for each in sub[index2]:if isinstance(each, int):each = [each]sub[index1].append(each + [value1])# 只保留以当前元素为终点的最长非递减子序列sub[index1][1:] = [max(sub[index1][1:], default=[], key=len)]sub = list(map(lambda items: max(items[1:],default=[],key=len),sub))return max(sub, key=len)def main():seed(20231106) # 填充种子,随机生成数据相同data = choices(range(1000), k = 35) # 从0-9999数据中随机取35个数据for func in (func3,func4,func5,func6):start = time() # 取LNDS前时刻for _ in range(1):r = func(data) # 类似与函数指针print(time()-start) # 打印取数耗时,单位msprint(r) # 打印LNDSif __name__ == '__main__':main()
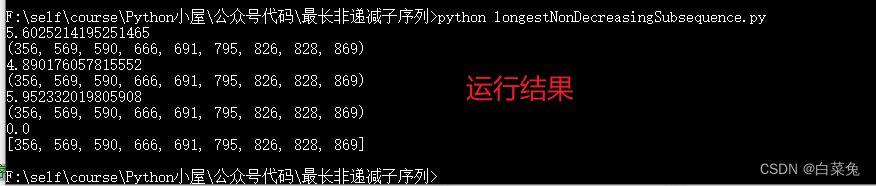
引用位置(不带注释):周末花了10小时把最长非递减子序列算法速度提高了几十亿倍