XoT：一种新的大语言模型的提示技术-编程知识

这是微软在11月最新发布的一篇论文，题为“Everything of Thoughts: Defying the Law of Penrose Triangle for Thought Generation”，介绍了一种名为XOT的提示技术，它增强了像GPT-3和GPT-4这样的大型语言模型(llm)解决复杂问题的潜力。

当前提示技术的局限性

LLM的最新进展通过将复杂的问题分解成更易于管理的“思想”，然后通过自然语言提示表达出来，从而实现了解决问题的新方法。但是大多数现有的提示技术都有局限性:

输入-输出(IO)提示仅适用于具有单步解决方案的简单问题，缺乏灵活性。

思维链(CoT)能够逐步解决问题，但仅限于线性思维结构，限制了灵活性。

思维树(ToT)和思维图(GoT)允许更灵活的思维结构，如树或图。但是它们需要LLM本身来评估中间思想，通过多个LLM调用产生大量的计算成本。

从本质上讲，当前的提示技术面临着“彭罗斯三角”约束——它们最多可以实现两个属性(性能、效率、灵活性)，但不能同时实现这三个属性。

XOT

为了解决这些限制，微软开发了一种新的提示技术，称为XOT (Everything of Thoughts)。XOT集成了强化学习和蒙特卡罗树搜索(MCTS)，将外部知识注入提示过程。这增强了llm的功能，并同时实现了更高的性能、效率和灵活性。

XOT的关键组件有:

MCTS模块-使用轻量级策略和价值网络，通过模拟有效地探索任务的潜在思想结构。

LLM求解器-利用LLM的内部知识对MCTS的思想进行提炼和修正。这种协作过程提高了“思维”质量。

XOT框架包括以下关键步骤:

预训练阶段:MCTS模块在特定任务上进行预训练，以学习有关有效思维搜索的领域知识。轻量级策略和价值网络指导搜索。

思想搜索:在推理过程中，预训练的MCTS模块使用策略/价值网络来有效地探索和生成LLM的思想轨迹。

思想修正:LLM审查MCTS的思想并识别任何错误。修正的想法是通过额外的MCTS模拟产生的。

LLM推理:将修改后的想法提供给LLM解决问题的最终提示。

下面的图表说明了XOT框架:

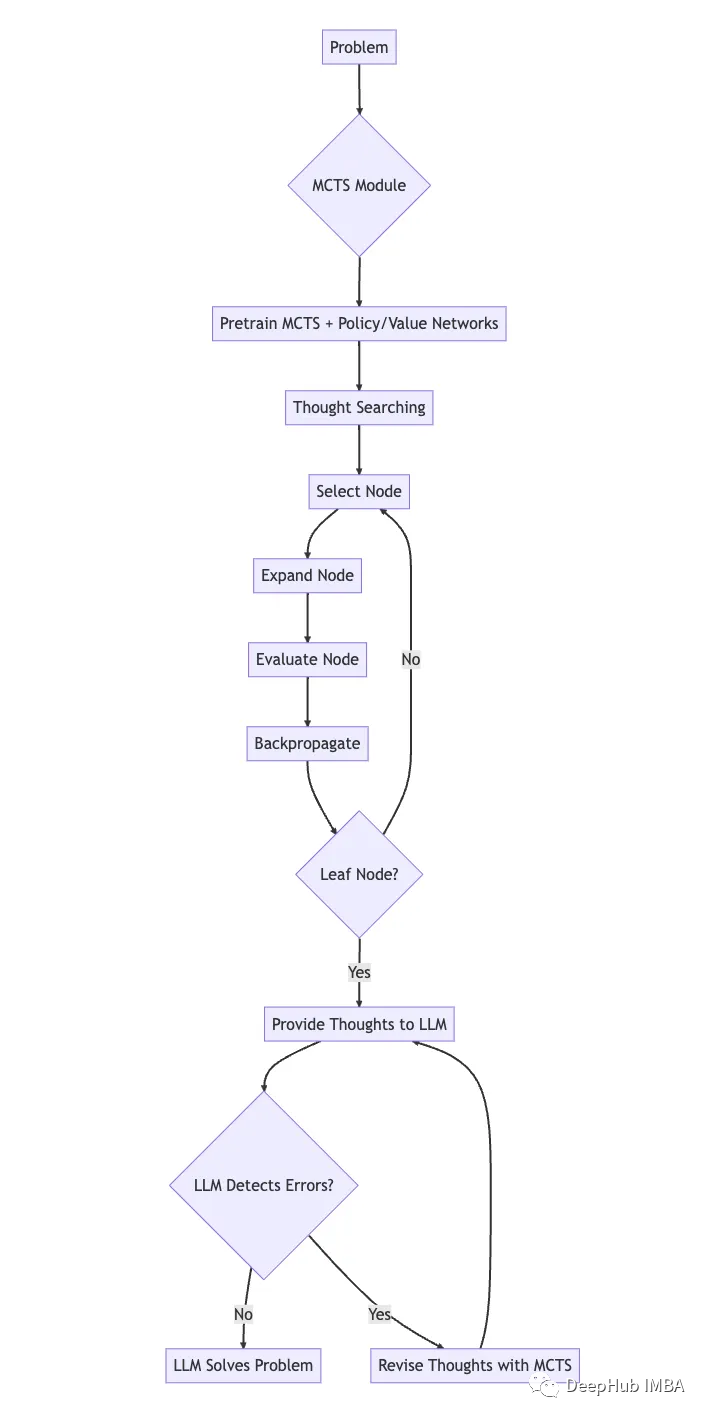
MCTS模块针对特定任务进行预训练，使用策略和价值网络来指导搜索和学习领域知识。

在思想搜索过程中，预训练的MCTS利用策略网络和价值网络有效地探索搜索空间并生成思想轨迹。这包括迭代地选择、展开、计算和反向传播节点。

思想轨迹提供给LLM作为提示。

LLM利用其内部知识来检测思想中的任何错误。如果发现错误，则使用MCTS模块通过额外的模拟来修改思想。

这个过程不断重复，直到LLM使用修改后的高质量思想解决问题。

XOT的一个示例

下面我们使用XOT解决Pocket Cube问题(一个2x2x2的魔方)来作为示例来介绍它是如何运作的

选择:算法从根节点开始，在当前状态下从可用的单步思想生成集中选择一个动作。这个过程一直持续到到达当前树中的一个叶节点。选择以PUCT算法为指导，目标是最大化上置信度界(UCB)。

评估和扩展:在到达先前未选择的叶节点时，会扩展到下一步进行新思想探索的状态。这种展开涉及到对状态的值和动作概率的评估，用θ参数化的神经网络建模，即(Pθ(s)， vθ(s)) = fθ(s)。其中Pθ(s)是s上所有动作的先验概率，vθ(s)表示其预测状态值。这两个值被保留和存储用于备份，状态被标记为“已访问”。

反向传播:随着叶子节点在上述阶段的扩展(可以是未探索状态，也可以是终端状态)，算法继续通过反向传播更新所有Q(s, a)值。对于未探索的节点，这种更新涉及计算其估计值vθ的平均值，而对于终止的节点，它是基于真实奖励r。这些更新发生在信息沿着轨迹反向传播到后续节点时。这里每个状态-操作对的访问计数也会增加。

思想推理:在MCTS完成搜索后，思想被提取并提供给LLM。LLM随后会对这些想法进行审查和提炼，如果需要，继续MCTS搜索过程，最终通过将这些外部想法与他们的内部知识相结合，形成最终的答案。

重复这个过程，直到问题得到解决或达到预定义的迭代次数。