文章目录
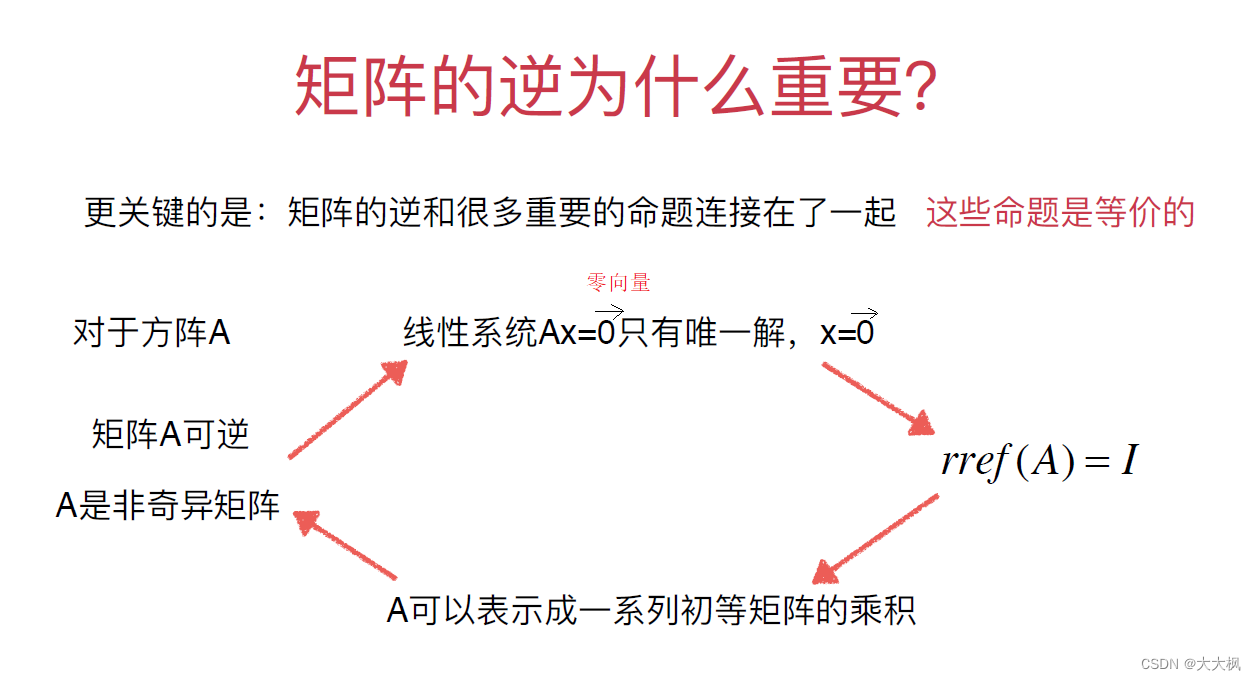
- 1 矩阵的逆
- 1.1 求解矩阵的逆
- 2 初等矩阵
- 2.1 初等矩阵和可逆性
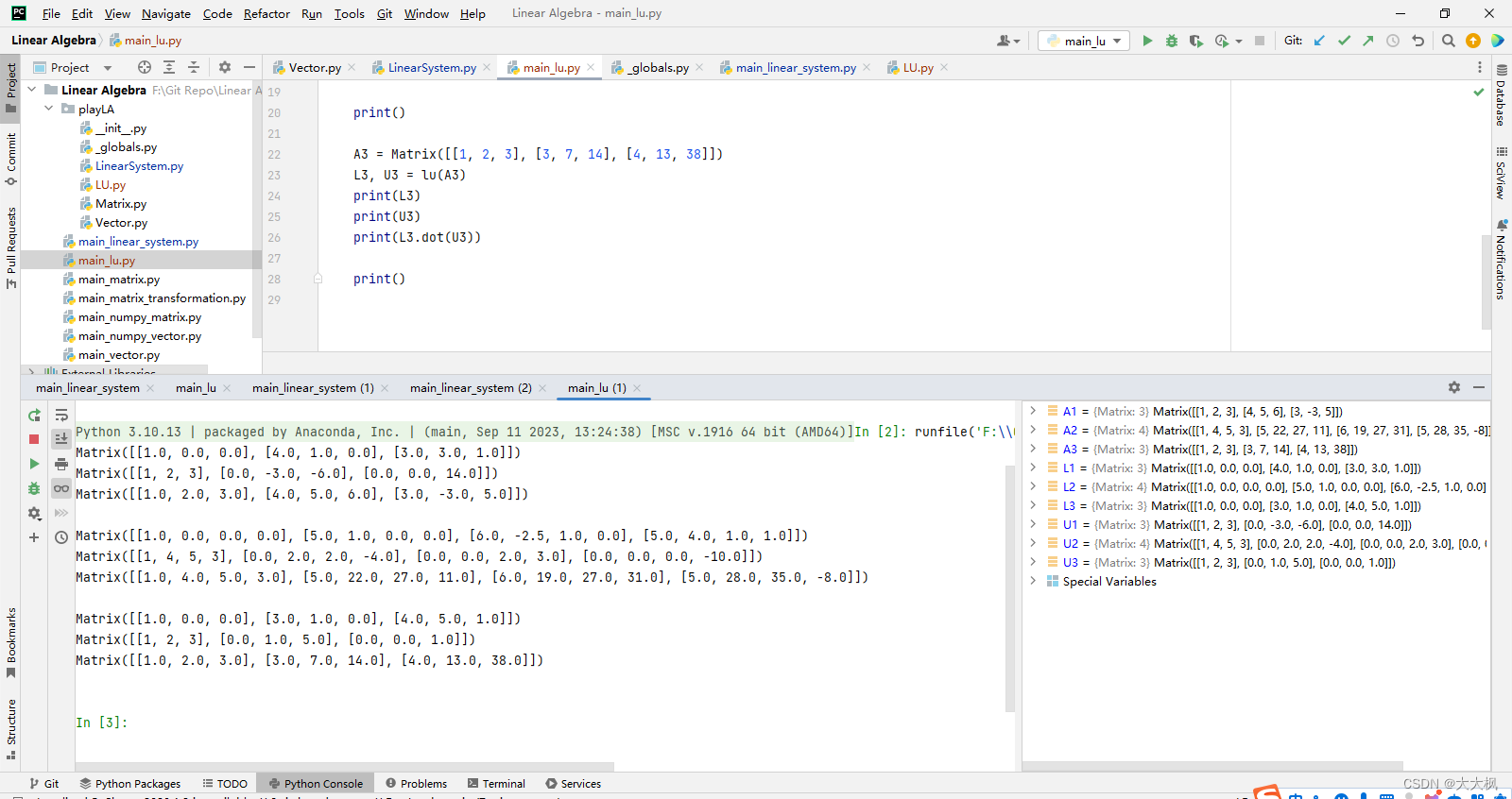
- 3 矩阵的LU分解
- 3.1 LU分解的实现
1 矩阵的逆

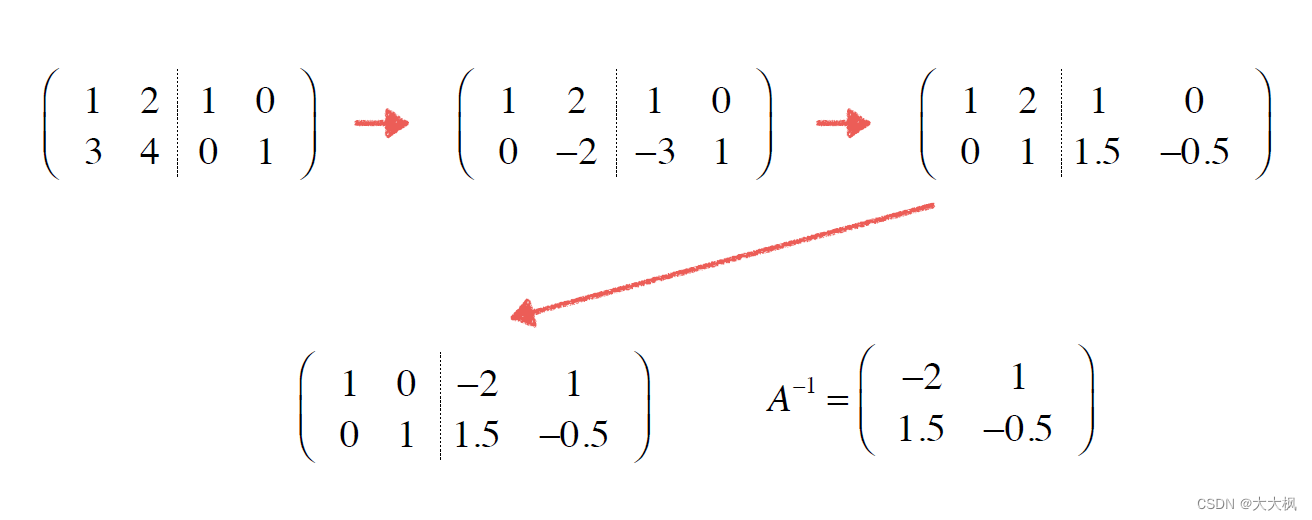
1.1 求解矩阵的逆
def inv(A):if A.row_num() != A.col_num():return Nonen = A.row_num()"""矩阵A+单位矩阵"""ls = LinearSystem(A, Matrix.identity(n))"""对线性系统进行高斯消元,如果没有解,返回none"""if not ls.gauss_jordan_elimination():return None"""高斯消元有解的话,把线性系统的右部分取出,重新构成矩阵,得到矩阵的逆"""invA = [[row[i] for i in range(n, 2*n)] for row in ls.Ab]return Matrix(invA)

2 初等矩阵


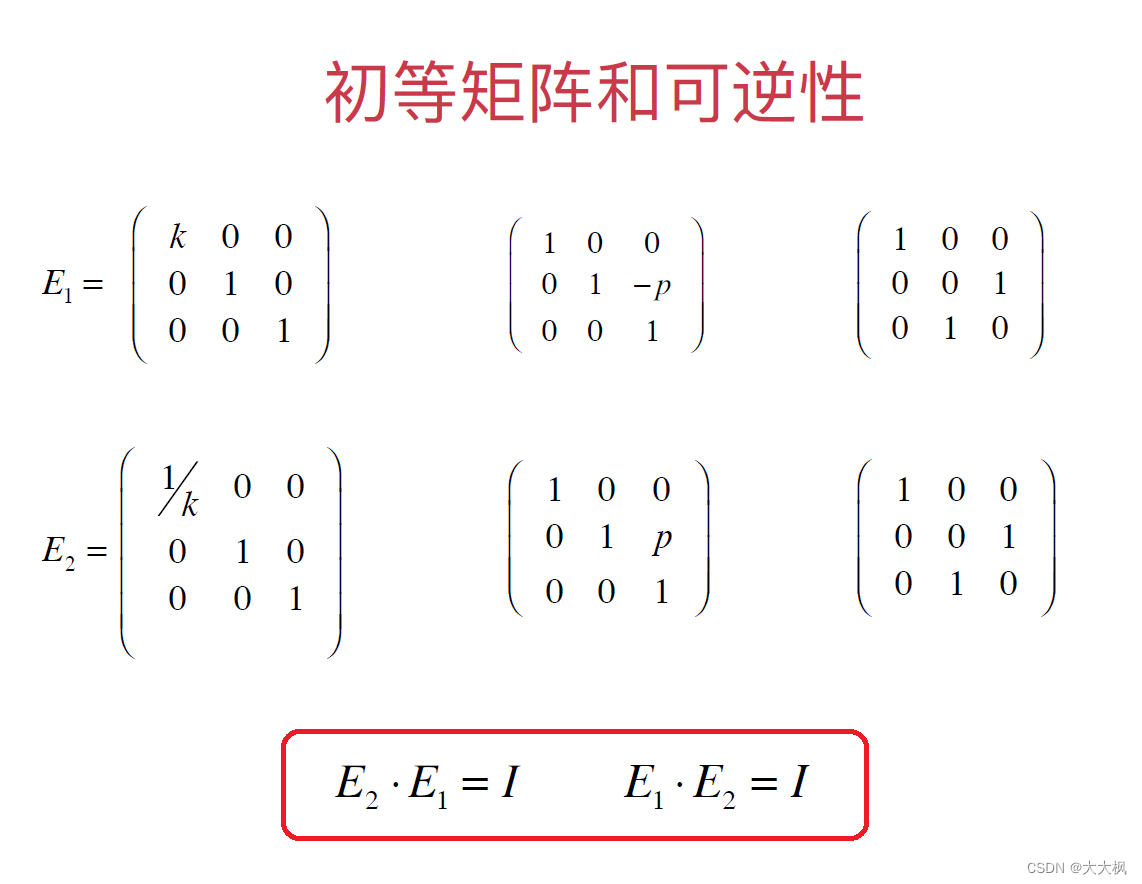
2.1 初等矩阵和可逆性
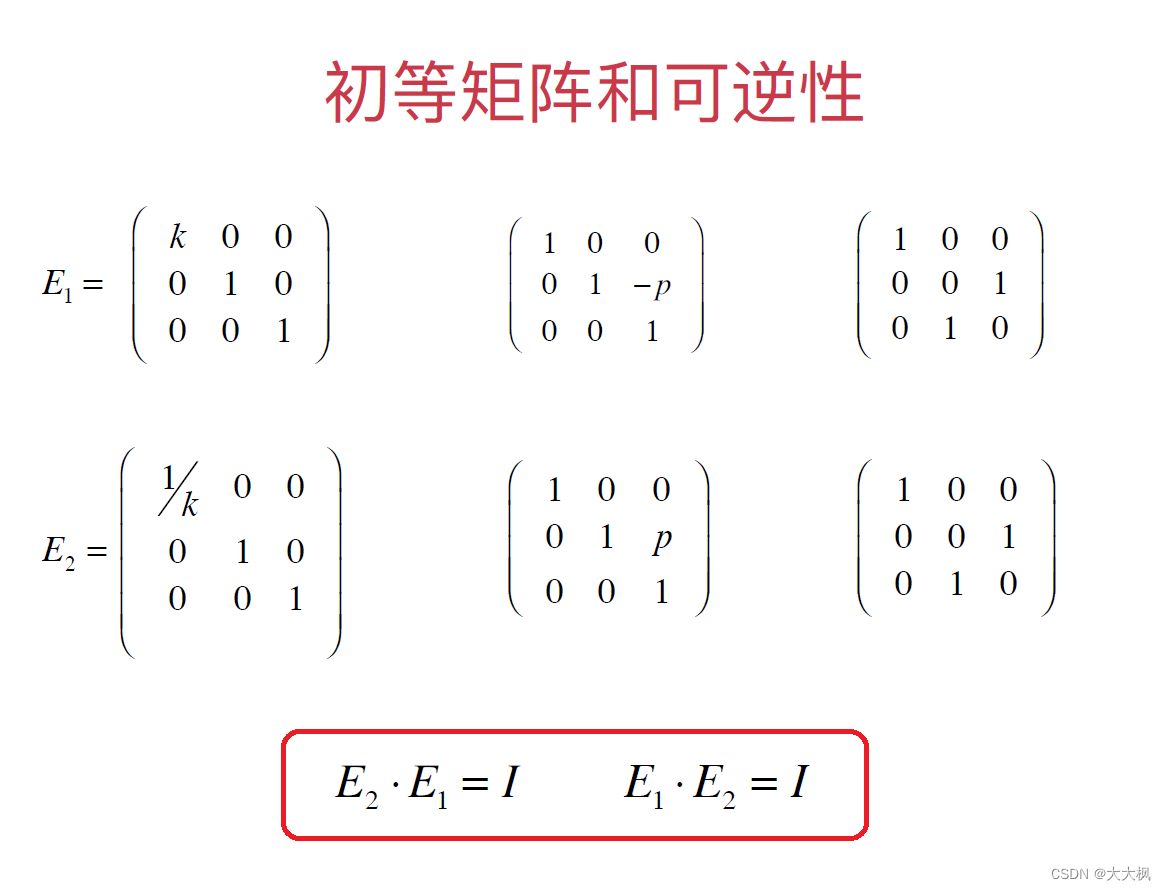

3 矩阵的LU分解
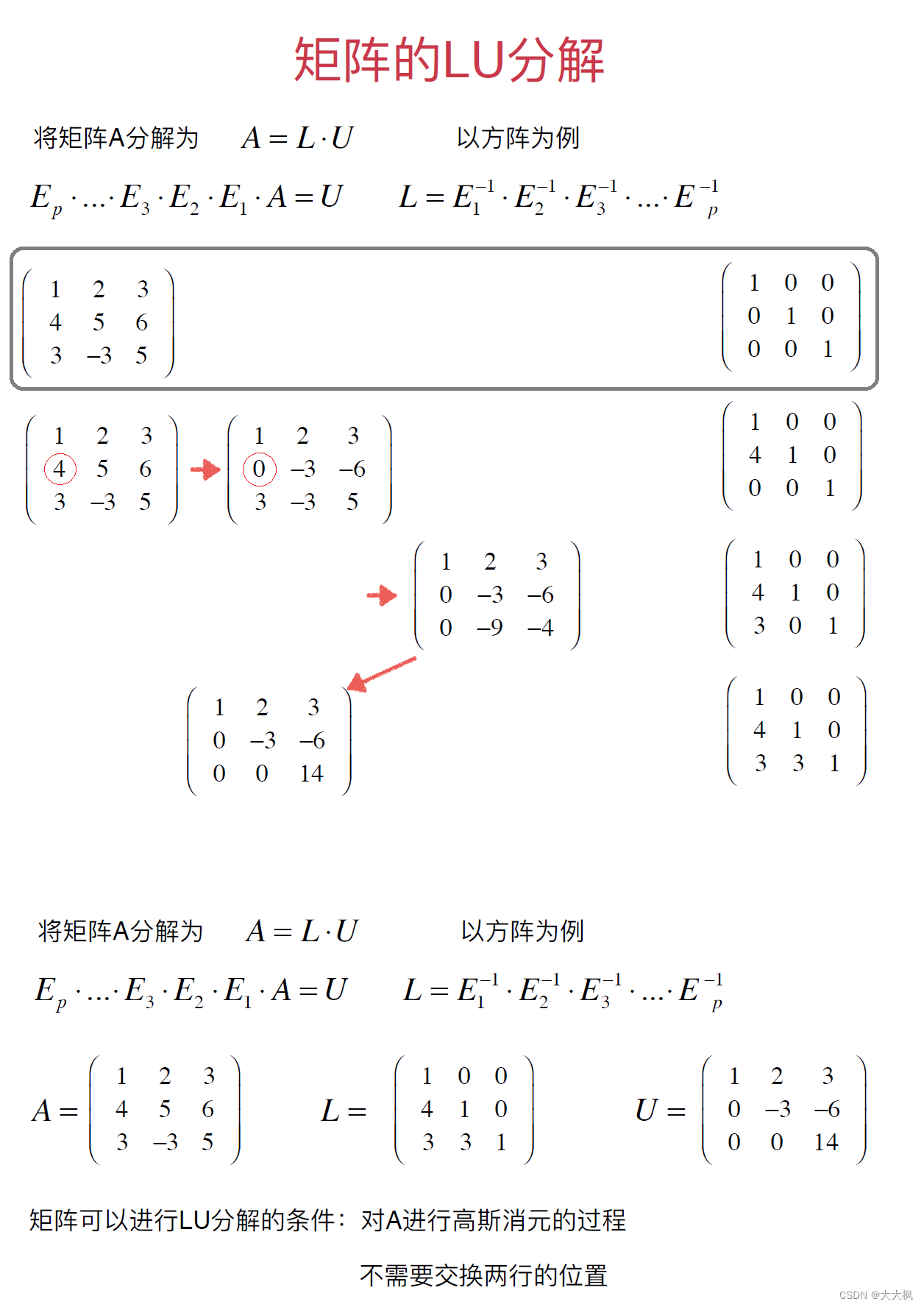
3.1 LU分解的实现
from .Matrix import Matrix
from .Vector import Vector
from ._globals import is_zerodef lu(matrix):assert matrix.row_num() == matrix.col_num(), "matrix must be a square matrix"n = matrix.row_num() """A是原矩阵的副本"""A = [matrix.row_vector(i) for i in range(n)]"""初始化L,使对角线元素为1"""L = [[1.0 if i == j else 0.0 for i in range(n)] for j in range(n)]for i in range(n):"""看A[i][i]位置是否可以是主元"""if is_zero(A[i][i]):return None, Noneelse: """将主元以下的j位置变为0"""for j in range(i + 1, n):p = A[j][i] / A[i][i] """求加减的系数"""A[j] = A[j] - p * A[i] """将第j行的位置经过加减运算变成0"""L[j][i] = p """将L矩阵相应位置变成相应变换的值"""return Matrix(L), Matrix([A[i].underlying_list() for i in range(n)])